X kvadrat

Vi forklarer hva som er x kvadrat, dens egenskaper, eksempler og øvelser løst

Området til en kvadrat med "x" side er x kvadrat. Kilde: f. Zapata.

Den algebraiske operasjonen av "X kvadrat"Det utføres ved å multiplisere mengden" x "med seg selv to ganger. Det er en del av potensieringsoperasjonene, og i matematiske symboler kommer det til uttrykk på denne måten:

x ∙ x = x²

Dette er et spesielt tilfelle av empowerment, der "x" representerer utgangspunkt Og "2" er eksponent. Hvis i en operasjon vises begrepet X², Den leser nøyaktig som "x kvadrat" eller "x firkantet".

Naturligvis er andre eksponenter mulig, for eksempel hvis eksponenten er 3, så er kraften skrevet som:

x ∙ x ∙ x = x³

Og les som "x til de tre", "X reist til kuben" eller bare "x til kuben".

Generelt kan eksponenten som basen er høy være et hvilket som helst tall, kalt "n", og i så fall er den tilsvarende kraften skrevet:

xⁿ = x ∙ x ∙ x ∙… ∙ x

Her indikerer suspensjonspunktene at "x" må multipliseres av seg selv "n", det vil si så mange ganger som eksponenten indikerer det.

Noen enkle eksempler på "x kvadrat", med tall, er følgende:

3² = 3 ∙ 3 = 9

(−4)² = (−4) ∙ (−4) = 16

Senere er forskjellige applikasjoner beskrevet som det er nødvendig.

Potensieringsegenskaper

Generelt sett kalles produktet av ethvert beløp med seg selv, n ganger, det kalles potensiering. Beregningen av X Squared er bare et spesielt tilfelle av potensiering, to andre tilfeller vises når du vil heve et beløp til Exponent 1, og som et resultat av samme beløp:

Kan tjene deg: Eksponentlover

Ettersom disse operasjonene er hyppige, for å jobbe med baser og eksponenter, blir noen enkle driftsregler fulgt, kalt Lover for eksponentene, som er oppført nedenfor:

Lover for eksponentene

I det følgende, "X" er basen og "n" og "m" er eksponentene.

1.- Produkt av like base krefter

Ved å multiplisere to (eller flere) krefter med lik base, oppnås basen til summen av eksponentene:

xⁿ∙ x^m = x^n+m

Når det gjelder X High, blir denne regelen brukt som følger, og erstatter N og M for 1:

x¹∙ x¹ = x¹⁺¹ = x²

2.- Powers Division of Equal Base

Ved å dele krefter av samme base, oppnås basen, hevet til subtraksjonen mellom de respektive eksponentene til telleren og nevneren:

xⁿ ÷ x^m = x^N-m

Ettersom divisjonen med 0 ikke er definert, må den oppfylles forutsatt at x ≠ 0.

3.- En kraft av en makt

Resultatet av kraften til en makt er lik basen som er forhøyet til produktets produkt:

(x^m)ⁿ = x^m∙n

Det kan oppnås igjen x kvadrat, når du gjør m = 1 og n = 2:

(x¹)² = x^1∙2 = x²

4.- Negativ eksponent

For negative eksponenter er operasjonen som skal utføres:

Når x ≠ 0. Merk at i dette tilfellet blir kraften en brøkdel med en teller som tilsvarer 1.

5.- Brøkeksponent

Fraksjonelle eksponenter kan skrives som den første roten til basen:

Under forutsetning av at n er forskjellig fra 0. Denne verdien blir rotindeksen, mens M blir eksponenten for mengden under roten, som i dette tilfellet er x.

Kan tjene deg: Hva er retningslinjen? (Geometri)

Produkter og kvotienter av forskjellige baser

Når du må forbedre produkter og kvoter av forskjellige "x" og "y" -baser, følges disse reglene:

1.- Produktkraft

For å utføre denne kraften heves hvert beløp til eksponenten N og det resulterende produktet er etablert:

(x ∙ y)ⁿ = xⁿ ⋅ ogⁿ

2.- Forholdet mellom kvotienten

Igjen må hvert beløp heves til eksponenten n separat og etablere kvotienten som resulterer, etter regelen om at beløpet "y" er forskjellig fra 0, i tilfelle av positive "n":

(x ÷ y)ⁿ = xⁿ ÷ yⁿ

Når "n" er negativ, må det tas forsiktighet, på grunn av eiendom 4 i forrige seksjon, blir telleren en nevner. I dette tilfellet må begge beløp være forskjellige fra 0, siden divisjonen med 0 må unngås for enhver pris.

Eksempler

Eksempel 1: Firkanter med naturlige tall

Torgene for de ti første naturlige tallene er:

• 1²= 1 × 1 = 1
• 2²= 2 × 2 = 4
• 3²= 3 × 3 = 9
• 4²= 4 × 4 = 16
• 5²= 5 × 5 = 25
• 6²= 6 × 6 = 36
• 7²= 7 × 7 = 49
• 8²= 8 × 8 = 64
• 9²= 9 × 9 = 81
• 10²= 10 × 10 = 100

Eksempel 2: Torget med negative tall

Torget til et negativt tall er alltid positivt, siden to mengder like tegn multipliseres, derfor:

(-x) · (-x) = x ∙ x = x²

For eksempel:

(-2) · (-2) = (-2)² = 4

Eksempel 3: Square of the Sum and Difference

Det er ofte nødvendig å beregne kvadratet av summen av to mengder, eller dens forskjell, operasjoner som er inkludert i kategorien bemerkelsesverdige produkter.

Operasjonen løses med indikasjonene som er gitt og hjelp av distribusjonseiendom:

Kvadrat for summen

La to "x" og "y" -beløp, og du vil finne kvadratet med summen (x + y)²:

Kan tjene deg: hierarki av operasjoner

(x + y)² = (x + y) ∙ (x + y) = x ∙ x + x ∙ y + y ∙ x + y ∙ y = x² + 2x ∙ y + og²

Dette uttrykket lyder slik: "Square of the First, pluss det doble produktet av det første for den andre pluss torget til den andre".

Firkant av forskjell

Det løses analogt, men tar hensyn til det negative tegnet:

(x - y)² = (x - y) ∙ (x - y) = x ∙ x - x ∙ y + y ∙ x - y ∙ y = x² - 2x ∙ og + og²

Eksempel 4: Området på et kvadrat

Torget er en 4 -sidig polygon, som har samme tiltak. La ℓ være sidemåling, deretter er område A på figuren gitt av:

A = ℓ²

Eksempel 5: Pythagoras teorem

Dette teoremet gjelder rektangeltrekanter, de som to av sidene danner rett vinkel. Disse sidene er kjent som "kategorier", og den gjenværende siden er "hypotenuse".

Teoremet slår fast at kvadratet til hypotenusa er lik summen av rutene til kategoriene. Teoremet kaller "a" og "b" til kategoriene, og "c" til hypotenusen, er teoremet skrevet som:

c² = a² + b²

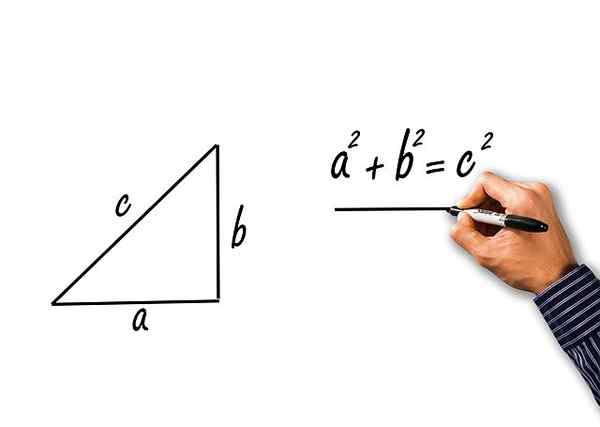Pythagoras teorem for et rektangelet trekant av katter a og b, og hypotenusa c

Løste øvelser

Oppgave 1

Beregn kvadratet til hypotenusen hvis ben måler 3 og 5 enheter.

Løsning

I følge Pythagoras 'teorem er kvadratet med hypotenusen:

c² = a² + b²

Erstatte verdiene:

c² = 3² + 5²= (3 × 3) + (5 × 5) = 9 + 25 = 34

Oppgave 2

Bestem området på en sidegruppe ℓ = 6 cm

Løsning

A = ℓ² = (6 cm)² = 36 cm²