Centripetal akselerasjonsdefinisjon, formler, beregning, øvelser

De centripetal akselerasjon til_c, Også kalt radial eller normal, det er akselerasjonen som bærer et mobilobjekt når du beskriver en sirkulær bane. Hans størrelse er v²/r, hvor r Det er sirkelens radius, den er rettet mot midten av den og er ansvarlig for at mobilen skal forbli i sin rute.

Dimensjonene til centripetal akselerasjon er lengde per enhetstid. I det internasjonale systemet er de M/S². Hvis centripetal -akselerasjonen av en eller annen grunn forsvinner, gjør også styrken som tvinger mobilen til å opprettholde den sirkulære banen.

De roterende objektene har centripetal akselerasjon, som er rettet mot midten av banen. Kilde: Pixabay

Dette er hva som skjer med en bil som prøver å gi en kurve på en flat- og frostspor, der friksjonen mellom gulvet og hjulene er utilstrekkelig slik at bilen tar kurven. Derfor er den eneste muligheten du har igjen å bevege seg i en rett linje, og det er derfor du kommer ut av kurven.

[TOC]

Sirkulære bevegelser

Når et objekt beveger seg i en sirkel, er til enhver tid centripetal -akselerasjonen radialt rettet mot midten av omkretsen, fulgte retning som er vinkelrett på banen.

Ettersom hastigheten alltid er tangent til banen, viser hastigheten og centripetal akselerasjon å være vinkelrett. Derfor har hastighet og akselerasjon ikke alltid samme retning.

Under disse omstendighetene har mobilen muligheten til å beskrive omkretsen med konstant eller variabel hastighet. Den første saken er kjent som Uniform eller MCU Circular Movement av sin forkortelse, den andre saken vil være en variabel sirkulær bevegelse.

Det kan tjene deg: Hva er utslippstørket? (Med eksempler)

I begge tilfeller er centripetal akselerasjon ansvarlig for å holde mobilen sirkler, og okkuperer at hastigheten bare varierer i retning og retning.

For å ha en variabel sirkulær bevegelse ville imidlertid en annen del av akselerasjon i samme hastighetsretning være nødvendig, noe som er ansvarlig for å øke eller synkende hastighet. Denne akselerasjonskomponenten er kjent som Tangensiell akselerasjon.

Den variable sirkulære bevegelsen og den krumlinjede bevegelsen generelt har begge komponentene i akselerasjonen, fordi den krumlinjede bevegelsen kan forestille seg som ruten gjennom utallige omkretsbuer som utgjør den buede banen.

Centripetal Force

Nå er en styrke ansvarlig for å gi akselerasjon. For en satellitt som går i bane rundt jorden, er det tyngdekraften. Og siden tyngdekraften alltid virker vinkelrett på banen, endrer den ikke hastigheten på satellitten.

I dette tilfellet fungerer tyngdekraften som en Centripetal Force, at det ikke er en spesiell klasse eller bortsett fra makt, men en som i tilfelle av satellitten, er radielt rettet mot jordens sentrum.

I andre typer sirkulær bevegelse, for eksempel en bil som tar en kurve, tolkes rollen som centripetal styrke av statisk rubbkraft som tvinger mobilen til å vende.

Formler for centripetal akselerasjon

Centripetal -akselerasjonen beregnes av uttrykket:

AC = v²/r

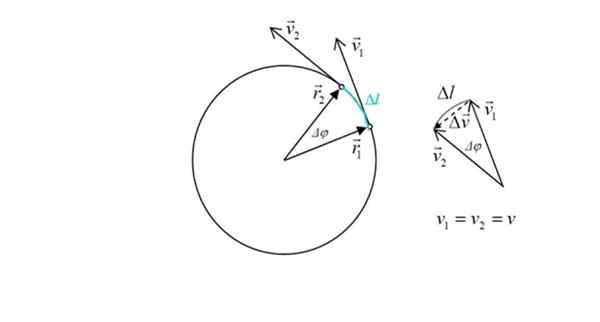Diagram for beregning av centripetal akselerasjon i en mobil med MCU. Kilde: Kilde: ILEVANAT [CC BY-SA 3.0 (https: // creativecommons.Org/lisenser/by-SA/3.0)]

Dette uttrykket vil bli trukket nedenfor. Per definisjon er akselerasjon variasjonen av hastighet i tid:

Det kan tjene deg: lyskilder: Typer og enheter som avgir lys

Toppdiagrammet viser i venstre figur, to punkter som en mobil passerer som beveger seg i en radiokrets r i antihorarium forstand. Legg merke til at hastigheten er den samme i begge tilfeller, men ikke retningen eller betydningen.

Mobilen bruker tid Δt På turen, som er liten, siden poengene er veldig nærme.

Figuren viser også to posisjonsvektorer r₁ og r₂, hvis modul er den samme: radioen r av omkretsen. Vinkelen mellom begge punktene er Δφ. I grønt Bue Tur til mobilen, betegnet som ΔL.

I figuren til høyre ser man at størrelsen på Δv, Endringen i hastigheten er omtrent proporsjonal med ΔL, siden vinkelen Δφ er liten. Men hastighetsendringen er nettopp relatert til akselerasjon. Trekanten blir advart, etter sum av vektorer om at:

v₁ + Δv = v₂ → Δv = v₂ - v₁

Δv Det er interessant, siden det er proporsjonalt med centripetal akselerasjon. Fra figuren blir det advart om at det å være liten vinkel Δφ, vektor Δv Det er i vinkelrett essens begge v₁ som v₂ og peker på sentrum av omkretsen.

Selv om vektorene skiller seg ut med fet skrift, for effekten av geometrisk natur som følger, jobber vi med modulene eller størrelsene på disse vektorene, uavhengig av vektornotasjon.

Noe annet: Du må bruke definisjonen av sentral vinkel, som er:

Δφ= Δl/r

Nå blir begge tallene sammenlignet, som er proporsjonale siden vinkelen Δφ det er vanlig:

Kan tjene deg: det som er polarisert lys?

 

Deling mellom ΔT:

 Siden definisjon av hastighet er v = ΔL/ ΔT. Men ΔV/ Δt Det er nettopp størrelsen på centripetal akselerasjon, som er det som søkes. På denne måten er uttrykket beskrevet i begynnelsen nådd:

til_c= v²/r

Trening løst

En partikkel beveger seg i en sirkel på 2.70 m radio. På et bestemt tidspunkt er akselerasjonen 1.05 m/s² I en retning som lager en vinkel på 32.0º med bevegelsesdirektoratet. Beregn hastigheten din:

a) På den tiden

b) 2.00 sekunder senere, forutsatt konstant tangentiell akselerasjon.

Svar

Det er en variert sirkulær bevegelse, siden uttalelsen indikerer at akselerasjonen har en gitt vinkel med retningen på bevegelsen som ikke er eller 0º (det kan ikke være en sirkulær bevegelse) eller 90º (det ville være en ensartet sirkulær bevegelse).

Derfor de to komponentene - radial og tangentiell - sameksistert. Vil bli betegnet som_c allerede_t og virker tegnet i følgende figur. Den grønne vektoren er nettoakselerasjonsvektoren eller bare akselerasjon til.

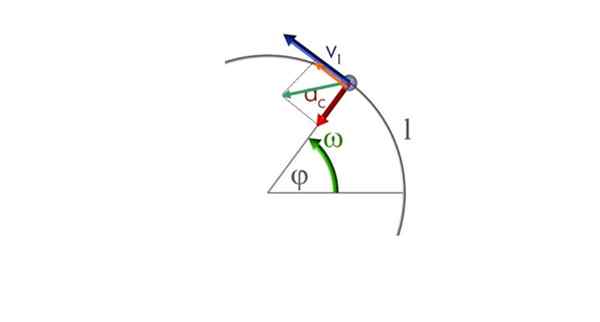En partikkel beveger seg i en sirkulær bane i antihorarisk forstand og variert sirkulær bevegelse. Kilde: Commons.Wikimedia.org

a) Beregning av akselerasjonskomponenter

til_c = a.cos θ = 1.05 m/s² . cos 32.0º = 0.89 m/s² (i rødt)

til_t = a.sin θ = 1.05 m/s² . Sen 32.0º = 0.57 m/s² (i oransje)

Beregning av mobilhastighet

Siden a_c = v²/r, så:
b) 2 sekunder senere hastigheten v vil bli økt takket være den tangensielle komponenten i akselerasjonen

v = v_enten +til_t. T = 1.6 m/s + (0.57 x 2) m/s = 2.74 m/s

Referanser

1. Giancoli, d. Fysikk. 2006. Prinsipper med applikasjoner. Sjette utgave. Prentice Hall. 107-108.
2. Hewitt, Paul. 2012. Konseptuell fysisk vitenskap. Femte utgave.Pearson.106 - 108.