Sannsynlighetsaksiomer, forklaring, eksempler, øvelser

De Axioms of sannsynlighet De er matematiske proposisjoner angående teorien om sannsynlighet, som ikke fortjener demonstrasjon. Axiomene ble opprettet i 1933 av den russiske matematikeren Andrei Kolmogorov (1903-1987) i sitt arbeid Grunnleggende om sannsynlighetsteori og la grunnlaget for den matematiske studien av sannsynlighet.

Når du utfører et visst tilfeldig eksperiment ξ, er prøveområdet det med sammen med alle mulige resultater av eksperimentet, også kalt arrangementer. Enhver hendelse er betegnet som A og P (A) er sannsynligheten for å skje. Da slo Kolmogorov det:

Figur 1. Sannsynlighetsaksiomer tillater å beregne sannsynligheten for å treffe pengespill som roulette. Kilde: Pixabay.

-Axioma 1 (ingen negativitet): Sannsynligheten for at enhver hendelse skjer er alltid positiv eller null, P (a) ≥0. Når sannsynligheten for en hendelse er 0, kalles den Umulig arrangement.

-Axioma 2 (sikkerhet): forutsatt at en eller annen hendelse som tilhører E, er sannsynligheten for forekomst 1, som vi kan uttrykke som P (e) = 1. Er det som er kjent som en Trygt arrangement, Siden når det utfører et eksperiment, er det et resultat med all sikkerhet.

-Axioma 3 (tillegg): I tilfelle av to eller flere inkompatible hendelser to til to, kalt til₁, TIL₂, TIL₃..., sannsynligheten for at hendelsen til₁ mer a₂ mer a₃ Og så videre er det summen av sannsynlighetene som hver og en skjer hver for seg.

Dette uttrykkes som: P (a₁ U a₂ U a₃ U ...) = p (a₁) + P (a₂) + P (a₃) +..

Figur 2. Den bemerkelsesverdige russiske matematikeren Andrei Kolmogorov (1903-1987), som la grunnlaget for aksiomatisk sannsynlighet. Kilde: Wikimedia Commons.

[TOC]

Eksempel

Sannsynlighetsaksiomer er mye brukt i mange applikasjoner. For eksempel:

En klør eller tachuela blir kastet i luften, og når gulvet faller, er det muligheten til å falle med spissen opp (u) eller med spissen ned (d) (vi vil ikke vurdere andre muligheter). Prøveområdet til dette eksperimentet består av disse hendelsene, deretter e = u, d.

Kan tjene deg: Revolution Faststoff: Volum, typer, løste øvelserFigur 3. I eksperimentet med å lansere Tachuela er det to hendelser med forskjellige sannsynligheter: fall med spissen opp eller på gulvet. Kilde: Pixabay.

Ved å bruke aksiomene vi har:

P (e) = 1 (Axioma 2)

Men P (E) = P (U) + P (D) (Axioma 3), fordi disse hendelsene er gjensidig inkompatible eller usammenhengende. Feilen faller ikke med spissen opp eller ned samtidig, det er det ene eller det andre, men ikke begge deler, siden andre muligheter blir vurdert. Så:

P (U) + P (D) = 1

P (u) = 1 - P (D)

Hvis det er like sannsynlig å falle med spissen opp eller ned, P (u) = p (d) = ½ (Axioma 1). Imidlertid kan det være at på grunn av konstruksjonen og utformingen av feilen. For eksempel kan det være det P (u) = ¾ samtidig som P (d) = ¼ (Axioma 1).

Merk at i begge tilfeller gir summen av sannsynlighetene 1. Aksiomer indikerer imidlertid ikke hvordan man tildeler sannsynligheter, i det minste ikke helt. Men de bekrefter at de er tall mellom 0 og 1, og at som forekommer i dette tilfellet, er summen av alle 1.

Måter å tildele sannsynlighet på

Sannsynlighetsaksiomer utgjør ikke en metode for å tildele verdien av sannsynlighet. For dette er det tre alternativer som er kompatible med aksiomer:

Laplace Rule

Hver hendelse tildeles samme sannsynlighet for å skje, da er sannsynligheten for forekomst definert som:

P (a) = antall tilfeller gunstig for hendelsen et antall mulige tilfeller

For eksempel hva er sannsynligheten for å trekke ut et ess fra et kortstokk med franske kort? Dekket har 52 kort, 13 av hver pinne og det er 4 pinner. Hver pinne har 1 som, så totalt er det 4 ess:

P (AS) = 4/52 = 1/13

Laplaces regel er begrenset til endelige prøveområder, der hver hendelse er like sannsynlig.

Kan tjene deg: diskret matematikk

Relativ frekvens

Her må eksperimentet være repeterbart, siden metoden er basert på å utføre et stort antall repetisjoner.

La oss gjøre repetisjoner av eksperimentet ξ, hvorav vi finner ut at N er antall ganger som oppstår en viss hendelse A, da er sannsynligheten for at denne hendelsen vil skje:

P (a) = lim_{I → ∞} (ingen)

Hvor n/i er den relative hyppigheten av en hendelse.

Definer P (a) på denne måten tilfredsstiller Kolmogorovs aksiomer, men det har ulempen at mange tester må utføres slik at sannsynligheten er passende.

Subjektiv metode

En person eller en gruppe mennesker kan gå med på å tildele sannsynligheten til en hendelse, gjennom sine egne dommer. Denne metoden har ulempen med at forskjellige mennesker kan tildele forskjellige sannsynligheter til samme hendelse.

Trening løst

I eksperimentet med samtidig lansering av 3 ærlige valutaer, og skaffet sjansene for hendelsene som er beskrevet:

a) 2 ansikter og et kors.

b) 1 ansikt og to kryss

c) 3 kryss.

d) minst 1 ansikt.

Løsning på

Ansiktene er betegnet med C og korsene med x. Men det er flere måter å få to ansikter og et kors. For eksempel kan de to første myntene falle med ansikt og den tredje med Cruz. Eller den første kan falle ansiktet, det andre korset og det tredje ansiktet. Og til slutt kan den første være et kors og de gjenværende ansiktene.

For å svare på spørsmålene er det nødvendig å kjenne alle mulighetene, som er beskrevet i et verktøy som heter trediagram enten Sannsynlighet tre:

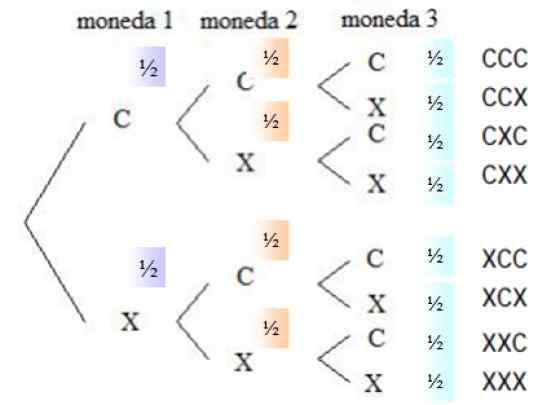Figur 4. Trediagram for samtidig lansering av tre ærlige mynter. Kilde: f. Zapata.

Sannsynligheten for at i enhver valuta er dyr er ½, skjer det samme for korsene, siden valutaen er ærlig. I høyre kolonne er alle mulighetene for lansering oppført, det vil si prøveområdet.

Kan tjene deg: statistiske variabler

Kombinasjonene som reagerer på den etterspurte hendelsen er valgt fra prøveområdet, siden ordren som ansiktene vises ikke er viktig. Det er tre gunstige hendelser: CCX, CXC og XCC. Sannsynligheten for hver hendelse er:

P (CCX) = ½. ½ . ½ = 1/8

Det samme skjer for CXC- og XCC -hendelser, hver og en har 1/8 sannsynlighet for å skje. Derfor er sannsynligheten for å oppnå nøyaktig 2 ansikter summen av sannsynligheten for alle gunstige hendelser:

P (2 ansikter) = 1/8 + 1/8 + 1/8 = 3/8 = 0.375

Løsning b

Å finne sannsynligheten for at det er nøyaktig to kryss er et analogt problem med det forrige, det er også tre gunstige hendelser hentet fra prøveområdet: CXX, XCX og XXC. Derfor:

P (2 kryss) = 3/8 = 0.375

Løsning c

Vet intuitivt at sannsynligheten for å oppnå 3 kryss (eller 3 ansikter) er lavere. I dette tilfellet er hendelsen som ble søkt xxx, på slutten av høyre kolonne, hvis sannsynlighet er:

P (xxx) = ½. ½. ½ = 1/8 = 0.125.

Løsning d

Det blir bedt om å få minst 1 ansikt, dette betyr at 3 ansikter, 2 ansikter eller 1 ansikt kan forlate. Den eneste hendelsen uforenlig med dette er en der 3 kryss kommer ut, hvis sannsynlighet er 0.125. Derfor er sannsynligheten som ble søkt:

P (minst 1 ansikt) = 1 - 0.125 = 0.875.

Referanser

1. Canavos, g. 1988. Sannsynlighet og statistikk: applikasjoner og metoder. McGraw Hill.
2. Devore, J. 2012. Sannsynlighet og statistikk for ingeniørfag og vitenskap. 8. Utgave. Cengage.
3. Lipschutz, s. 1991. Schaum Series: Sannsynlighet. McGraw Hill.
4. Obregón, i. 1989.Teori om sannsynlighet. Redaksjonell Limusa.
5. Walpole, r. 2007. Sannsynlighet og statistikk for ingeniørfag og vitenskap. Pearson.