Balanse av materie hva som er, generell ligning, typer

Han materialbalanse Det er tellingen av komponentene som tilhører et system eller en prosess som studeres. Denne balansen kan brukes nesten på alle typer systemer, siden det antas at summen av massene av slike elementer må forbli konstant til forskjellige målinger av målinger.

Du kan forstå av komponent til klinkekuler, bakterier, dyr, tømmer, ingredienser til en kake; og i tilfelle av kjemi, molekyler eller ioner, eller mer spesifikt, forbindelser eller stoffer. Deretter må den totale massen av molekylene som kommer inn i et system, med eller uten kjemisk reaksjon forbli konstant; Så lenge det ikke er noen lekkasjetap.

I praksis blir utallige problemer presentert som kan påvirke balansen mellom materie, i tillegg til å ta hensyn til forskjellige fenomener av materie og effekten av mange variabler (temperatur, trykk, strømning, omrøring, reaktorstørrelse, etc.).

På papiret må imidlertid beregningene av sakbalansen sammenfalle; det vil si at massen av kjemiske forbindelser ikke skal forsvinne når som helst. Å gjøre denne balansen er analog for å sette en haug med bergarter i balanse. Hvis en av massene kommer malplassert, faller alt fra hverandre; I dette tilfellet vil det bety at beregningene er gale.

Generell emnebalanse ligning

I hvert system eller prosess må det først defineres hva grensene deres er. Fra dem vil det være kjent hvilke forbindelser som kommer inn eller forlater. Det er praktisk å gjøre det, spesielt hvis det er flere prosessenheter å vurdere. Når alle enheter eller delsystemer blir vurdert, er det snakk om en balanse av generell materie.

Denne balansen har en ligning, som kan brukes på ethvert system som adlyder loven om massebevaring. Ligningen er som følger:

Kan tjene deg: blyklorid: egenskaper, struktur, bruk

E + G - S - C = A

Hvor e er mengden av materie som kommer inn Til systemet; G er det jeg vet generere hvis en kjemisk reaksjon oppstår i prosessen (som i en reaktor); S er hva kommer ut av systemet; C er det jeg vet forbruke, Igjen, hvis det er en reaksjon; Og til slutt er det det jeg vet akkumulerer.

Forenkling

Hvis det i systemet eller prosessen som studeres, er det ingen kjemisk reaksjon, G og C er verdt null. Dermed gjenstår ligningen:

E - s = a

Hvis systemet også blir vurdert i stasjonær tilstand, uten betydelige endringer i variablene eller strømningene til komponentene, sies det at ingenting akkumuleres inne. Derfor er det verdt null, og ligningen ender opp med å forenkle enda mer:

E = s

Det vil si at mengden av materie som kommer inn er lik den som kommer ut. Ingenting kan gå tapt eller forsvinne.

På den annen side, hvis det er en kjemisk reaksjon, men systemet er i stasjonær tilstand, vil G og C ha verdier og vil fortsette å være null:

E + G - S - C = 0

E + G = S + C

Noe som betyr at i en reaktor er massen av reagensene som kommer inn og av produktene som genererer i den, lik massen til produktene og reagensene som kommer ut, og av reagensene som konsumeres.

Eksempel på bruken: Fisk i elven

Anta at antallet fisk i en elv blir studert, hvis bredder kommer til å representere grensen til systemet. Det er kjent at i gjennomsnitt 568 FISH ENTER per år, 424 blir født (generere), 353 die (konsumer) og 236 emigrerer eller permisjon.

Bruke den generelle ligningen har du:

568 + 424 - 353 - 236 = 403

Dette betyr at de med 403 fisk de akkumuleres i elven; det vil si per år elven beriker mer fisk. Hvis jeg hadde en negativ verdi, ville det bety at antallet fisk synker, kanskje til negative miljøpåvirkninger.

Det kan tjene deg: ionisk kraft: enheter, hvordan beregne det, eksempler

Folkens

Fra den generelle ligningen kan du tro at det er fire ligninger for forskjellige typer kjemiske prosesser. Imidlertid er sakbalansen delt inn i to typer i henhold til et annet kriterium: tid.

Differensialbalanse

I balansen mellom differensialstoff er det mengden av komponentene i et system på et gitt tidspunkt eller tid. Disse massemengdene kommer til uttrykk med tidsenheter, og representerer derfor hastigheter; For eksempel kg/t, som indikerer hvor mange kilometer som kommer inn, forlater, akkumulerer, genererer eller konsumerer på en time.

Slik at det er masse (eller volumetriske strømmer, med tettheten for hånden), må systemet generelt være åpent.

Integrert balanse

Når systemet er lukket, som med reaksjonene som er utført i intermitterende reaktorer (batchtype), interesserer massene av dets komponenter vanligvis før og etter prosessen; det vil si blant de første og siste t -tidene.

Derfor uttrykkes mengder som bare masser og ikke hastigheter. Denne typen balanser lages mentalt når en blender brukes: Massen til ingrediensene som kommer inn må være lik den som er igjen etter motoren.

Eksempeløvelse

Det er ønsket å fortynne en strømning av en 25% metanoloppløsning i vann, med en annen av en 10% konsentrasjon, mer fortynnet, på en slik måte at 100 kg/t genereres fra en 17% metanoloppløsning. Hvor mye av begge metanolløsningene, på 25 og 10%, må gå inn i systemet i timen for å oppnå dette? Anta at systemet er i stasjonær tilstand

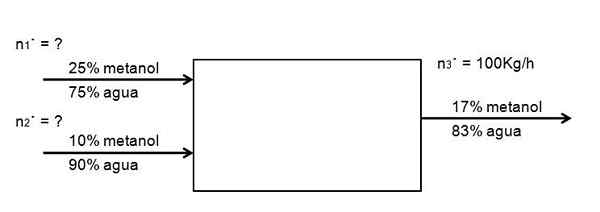
Kan tjene deg: Forlengelse

Følgende diagram eksemplifiserer uttalelsen:

Flowdiagram for fortynning av fortynning av metanoloppløsningen. Kilde: Gabriel Bolívar.

Det er ingen kjemisk reaksjon, så mengden metanol som kommer inn må være lik den som kommer ut:

OG_Metanol = S_Metanol

0,25 n₁^· + 0,10 n₂^· = 0,17 n₃^·

Bare verdien av n er kjent₃^·. Resten er ukjente. For å løse denne ligningen av to ukjente, er det nødvendig med en annen balanse: vannet. Så er det å lage samme balanse for vann:

0,75 n₁^· + 0,90 n₂^· = 0,83 n₃^·

Verdien av n blir fjernet for vann₁^· (Det kan også være n₂^·):

n₁^· = (83 kg/t - 0,90n₂^·)/ (0,75)

Erstatter da n₁^· I saken balanserer ligning for metanol, og løsning for n₂^· Du har:

0,25 [(83 kg/t - 0,90N₂^·)/ (0,75)] + 0,10 n₂^· = 0,17 (100 kg/t)

n₂^· = 53,33 kg/t

Og å oppnå n₁^· Bare trekk:

n₁^· = (100-53,33) kg/t

= 46,67 kg/t

Derfor må du i timen legge inn 46,67 kg -systemet med 25%metanoloppløsning, og 53,33 kg av 10%-løsningen.

Referanser

1. Felder og Rousseau. (2000). Elementære prinsipper for kjemiske prosesser. (Andre utgave.). Addison Wesley.
2. Fernández Germán. (20. oktober 2012). Definisjon av materiebalanse. Gjenopprettet fra: Industri.nett