Matematisk biologihistorie, studieobjekt, applikasjoner

De Matematisk biologi eller biomatematikk er en gren av vitenskap som er ansvarlig for utviklingen av numeriske modeller som klarer å simulere forskjellige naturfenomener relatert til levende vesener; det vil si at det innebærer bruk av matematiske verktøy for å studere naturlige eller biologiske systemer.

Som det kan forstås i navnet sitt, er biomatematikk et tverrfaglig område, som er i skjæringspunktet mellom kunnskap mellom biologi og matematikk. Et enkelt eksempel på denne disiplinen kan omfatte utvikling av statistiske metoder for å løse problemer innen genetikk eller epidemiologi, for å nevne noen.

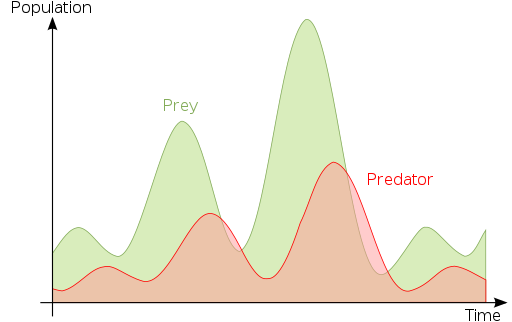Lotka-Volterra Law for forholdet mellom rovdyr og demninger (kilde: Curtis Newton ↯ 10:55, 20. Apr. 2010 (cest).Den opprinnelige opplasteren var lämpel på tysk wikipedia. [CC By-SA 3.0 (http: // creativecommons.Org/lisenser/by-SA/3.0/)] via Wikimedia Commons)

På dette kunnskapsområdet er det normalt at matematiske resultater oppstår fra biologiske problemer eller brukes til å løse dem, men noen forskere har klart å løse matematiske problemer basert på observasjon av biologiske fenomener, så det er ikke et ensrettet forhold mellom Begge vitenskapsfeltene.

Fra det ovennevnte kan det sikres at et matematisk problem er slutten som biologiske verktøy og omvendt brukes til; At et biologisk problem er slutten som de veldig varierte matematiske verktøyene brukes.

For tiden vokser feltet med matematisk biologi ved akselererte trinn og regnes som en av de mest moderne og spennende applikasjonene i matematikk. Det er veldig nyttig ikke bare innen biologi, men i biomedisinske vitenskaper og innen bioteknologi.

[TOC]

Biomatematikkhistorie

Matematikk og biologi er to vitenskaper med mangfold av applikasjoner. Matematikk er kanskje like gammel som vestlig kultur, opprinnelsen stammer tilbake mange år før Kristus, og dens nytteverdi har blitt demonstrert siden den gang for et stort antall applikasjoner.

Kan tjene deg: Oksidasetest: Foundation, Procedure and Uses

Biologi som vitenskap er imidlertid mye nyere, siden konseptualiseringen ikke skjedde før begynnelsen av 1800 -tallet takket være intervensjonen fra Lamarck, for 1800 -tallet.

Forholdet mellom matematisk og biologisk kunnskap er smalt siden de tidlige stadiene av sivilisasjoner, siden bosettingen av nomadiske folk fant sted takket være oppdagelsen at naturen kan utnyttes systematisk, noe som må ha obligatorisk de første forestillingene matematikk og biologisk.

I sine prinsipper ble biologiske vitenskaper betraktet som "håndverk", siden de hovedsakelig henviste til populære aktiviteter som landbruk eller husdyr; I mellomtiden oppdaget matematikken abstraksjon og hadde noen fjerne applikasjoner.

Samløpet mellom biologi og matematikk stammer fra det femtende og sekstende århundre, med bruk av fysiologi, som er en vitenskap som grupperer kunnskap, klassifiserer dem, bestiller dem og systematiserer dem som bruker matematiske verktøy når det er nødvendig.

Thomas Malthus

Det var Thomas Malthus, en moderne økonom med Lamarck, som la presedensen for begynnelsen av matematisk biologi, siden han var den første som postulerte en matematisk modell for å forklare populasjonsdynamikk basert på naturressurser.

Malthuss tilnærminger ble deretter mer utviklet og utdypet, og i dag er en del av grunnlaget for økologiske modeller som brukes til å forklare forholdet mellom rovdyr og deres byttedyr, for eksempel.

Objekt for studie av matematisk biologi

Matematisk biologi er et tverrfaglig vitenskapelig område. Kilde: Konstantin Kolosov - Pixabay

Matematisk biologi er en vitenskap som følger av integrering av forskjellige matematiske verktøy med biologiske, eksperimentelle eller ikke, som søker å dra nytte av "kraften" av matematiske metoder for bedre å forklare levende vesener, deres celler og av dens molekyler.

Det kan tjene deg: næringskjede: elementer, trofisk pyramide og eksempler

Uansett grad av teknologisk kompleksitet involvert, består matematisk biologi av den "enkle" vurderingen av at det er en analogi mellom to prosesser, nemlig:

- Den komplekse strukturen i et levende vesen er resultatet av anvendelsen av enkel "kopiert" og "kutt og spleising" eller "Splicing”(For eksempel) til innledende informasjon som er inneholdt i en DNA -sekvens (deoksyribonukleinsyre) -sekvens.

- Resultatet F (Ω) for anvendelsen av en beregbar funksjon på en ordning W kan oppnås ved å bruke en kombinasjon av enkle grunnleggende funksjoner til W.

Feltet for matematisk biologi bruker områder av matematikk som beregning, sannsynlighetsteorier, statistikk, lineær algebra, algebraisk geometri, topologi, differensialligninger, dynamiske systemer, kombinatorisk og kodingsteori.

Nylig har denne disiplinen blitt veldig utnyttet for den kvantitative analysen av forskjellige typer data, ettersom biologiske vitenskaper har dedikert seg til store datamasser som informasjonen kan hentes ut verdifull.

Faktisk vurderer mange forskere at den store eksplosjonen av biologiske data "skapte" behovet for å utvikle nye og mer komplekse matematiske modeller for analyse, så vel som beregningsalgoritmer og betydelig mer komplekse statistiske metoder.

applikasjoner

En av de mest betydningsfulle anvendelsene av matematisk biologi har å gjøre med analysen av DNA -sekvenser, men denne vitenskapen er også involvert i modellering av epidemier og i studiet av forplantning av nervesignaler.

Det har blitt brukt til studiet av nevrologiske prosesser som Parkinsons sykdom, Alzheimers og amyotrofe lateral sklerose, for eksempel.

Kan tjene deg: erytrous: egenskaper, struktur, funksjoner

Det er veldig nyttig for studiet av evolusjonsprosesser (teoretiseringer) og for utvikling av modeller som forklarer forholdet mellom levende vesener og deres miljø, det vil si for økologiske tilnærminger.

Modellering og simulering av forskjellige typer kreftformer er også et godt eksempel på de flere applikasjonene som matematisk biologi har i dag, spesielt med tanke på simulering av interaksjoner mellom cellulære populasjoner.

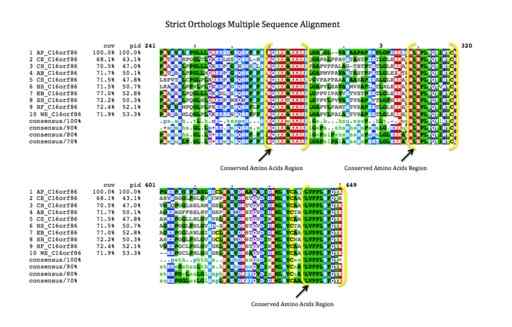Eksempel på analysen av DNA-sekvensene som vanligvis brukes i genomikken (kilde: RADTK172 [CC BY-SA 4.0 (https: // creativecommons.Org/lisenser/by-SA/4.0)] via Wikimedia Commons)

Biomathematics er også veldig avansert innen beregningsmessig nevrovitenskap, i studier av populasjon og fylogenomisk og genomisk dynamikk generelt.

I denne siste grenen av genetikk har det vært av stor relevans, siden det er et av de høyeste vekstområdene de siste årene, siden frekvensen av datainnhenting er ekstremt høy, noe som fortjener nye og bedre teknikker for behandlingen og analysen.

Referanser

1. Andersson, s., Larsson, k., Larsson, m., & Jacob, m. (Eds.). (1999). Biomatematikk: Matematikk av bioslaturer og biodynamikk. Elsevier.
2. Elango, p. (2015). Matematikkens rolle i biologi.
3. Friedman, a. (2010). Hva er matematisk biologi og hvor nyttig er den. Varsler om AMS, 57 (7), 851-857.
4. Hofmeyr, J. H. S. (2017). Matematikk og biologi. South African Journal of Science, 113 (3-4), 1-3.
5. Kari, l. (1997). DNA -databehandling: Ankomst av biologisk matematikk. Matematisk intelligencer, 19 (2), 9-22.
6. Pacheco Castelao, J. M. (2000). Hva er matematisk biologi?
7. Reed, m. C. (2004). Hvorfor er Mathematico Biology så hard? Varsler om AMS, 51 (3), 338-342.
8. Ulam, s. M. (1972). Underideer og utsikter i biomatematikk. Årlig gjennomgang av biofysikk og bioingeniør, 1 (1), 277-292.