Radiell belastning hvordan beregnes, løste øvelser

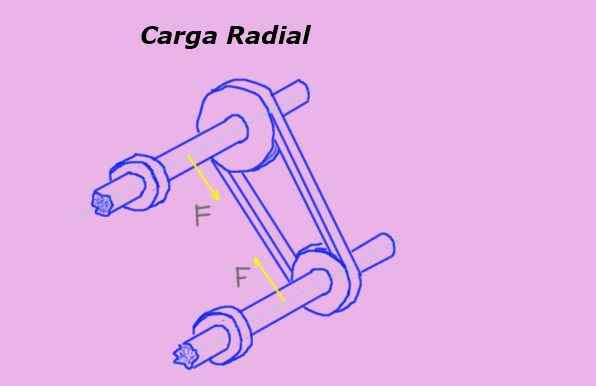
De Radial belastning Det er kraften som utøves vinkelrett på symmetriaksen til et objekt og hvis handlingslinje passerer gjennom denne aksen. For eksempel pålegger et belte på en remskive en radiell belastning på lageret eller lager av aksen til den samme.

I figur 1 representerer de gule pilene radiale krefter på aksene på grunn av belteens spenning som passerer gjennom remskivene.

Figur 1. Radial belastning på remskivøkser. Kilde: Selvlaget.

Målingsenheten for den radielle belastningen i det internasjonale systemet eller hvis det er Newton (N). Men andre kraftenheter brukes også til å måle den, for eksempel kilogramkraften (kg-f) og pundstyrken (LB-F).

[TOC]

Hvordan beregnes det? 

For å beregne verdien av den radielle belastningen i elementene i en struktur, må følgende trinn følges:

- Lage kreftene diagrammet på hvert element.

- Bruk ligningene som garanterer translasjonsbalansen; det vil si at summen av alle kreftene er null.

- Tenk på ligningen av dreiemomenter eller øyeblikk slik at rotasjonsbalansen blir oppfylt. I dette tilfellet må summen av alle moment være null.

- Beregn kreftene for å identifisere de radielle belastningene som virker i hvert av elementene.

Løste øvelser

-Oppgave 1

Følgende figur viser en remskive som en anspent remskive passerer med spenning t. Remskiven er montert på en akse som hviler på to chumaceras. Sentrum for en av dem er på avstand l₁ fra midten av remskiven. I den andre enden er den andre Chumacera, på en avstand l₂.

Kan tjene deg: Higroskopisitet: konsept, hygroskopiske stoffer, eksempler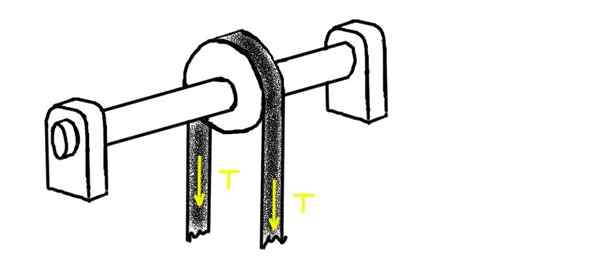Figur 2. Remskive som en anspent stropp passerer. Kilde: Selvlaget.

Bestem den radielle belastningen på hver av Chumaceras, forutsatt at vekten på aksen og remskiven er ganske lavere enn påført spenning.

Ta som verdi for 100 kg-f stroppspenningen og for avstander l₁= 1 m og l₂= 2 m.

Løsning

For det første blir det laget et diagram over kreftene som virker på aksen.

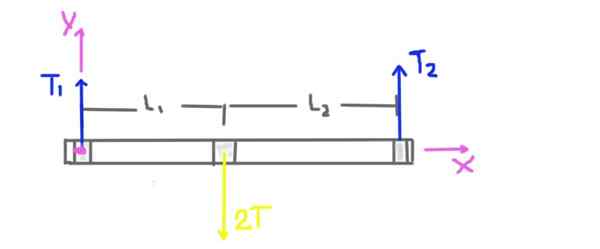Figur 3. Treningskrefter Diagram 1.

Remskiven er t, men den radielle belastningen på aksen i remskiven er 2t. Vekten på aksen og remskiven blir ikke tatt i betraktning fordi problemuttalelsen forteller oss at den er mye lavere enn spenningen som påføres beltet.

Den radiale reaksjonen av støtten støtter er forårsaket av de radiale kreftene eller laster T1 og T2. Avstandene L1 og L2 av støttene til midten av remskiven er også indikert i diagrammet.

Koordinatsystemet vises også. Dreiemomentet eller det totale øyeblikket på aksen vil bli beregnet som et sentrum opprinnelsen til koordinatsystemet og vil være positiv i z -retningen.

Likevektsforhold

Likevektsforholdene er nå etablert: summen av samme null og summen av dreiemomenter like null.

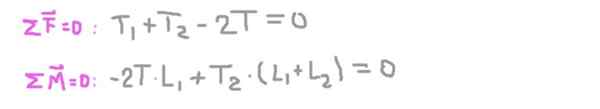
Fra den andre ligningen₂), erstatte den første og rydde den radiale reaksjonen på aksen i støtte 1 (t₁).

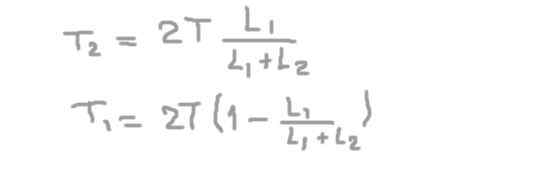Hvis vi erstatter de numeriske dataene, oppnår vi at den radielle belastningen eller kraften på aksen i støtteposisjonen 1 er:

T₁= (2/3) t = 66,6 kg-f

Det kan tjene deg: Kalibreringskurve: Hva er det for, hvordan du gjør det, eksempler

Og den radielle belastningen på aksen til støtte for støtte 2 er:

T₂= (4/3) t = 133,3 kg-f.

Oppgave 2

Følgende figur viser et system sammensatt av tre remskiver a, b, c alle radio r. Klassene er koblet sammen med et belte som har en T -spenning.

Axes A, B, C Pass smørte lagre. Separasjonen mellom sentrene til aksene A og B er 4 ganger radius r. Tilsvarende er separasjonen mellom aksene B og C også 4R.

Bestem den radielle belastningen på aksene på remsklassene A og B, forutsatt at spenningen på beltet er 600n.

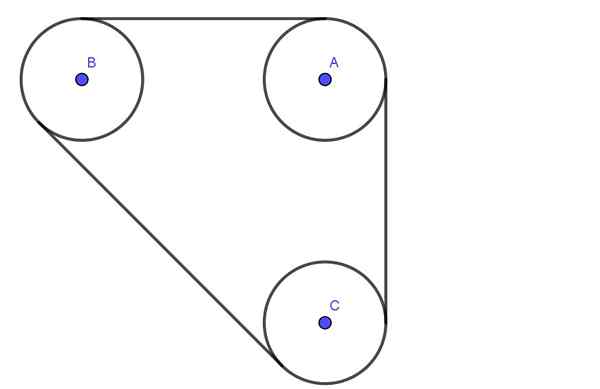Figur 4. Remskivesystem. Oppgave 2. (Egen utdyping)

Løsning

Det begynner med å tegne et diagram over kreftene som virker på remskive A og B. På den første har du begge T -spenningene₁ og T₂, så vel som styrken f_TIL At lageret utøver på remskiven.

Tilsvarende har du på remskive B spenninger t₃ , T₄ og styrken f_B at lageret utøver på aksen til det samme. Den radielle belastningen på remskiven A er kraften f_TIL og den radielle belastningen på B er kraften f_B.

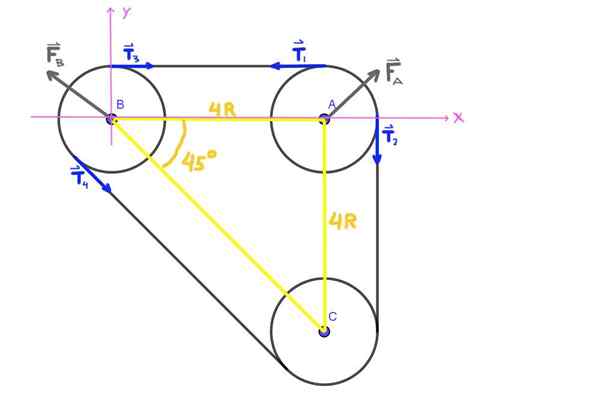Figur 5. Krefter diagram, oppgave 2. (Egen utdyping)

Ettersom akser A, B, C danner en isorektangle -trekant, er ABC -vinkelen 45 °.

Alle spenninger t₁ , T₂ , T₃ , T₄ vist på figuren har samme modul T, som er beltespenningen.

Balansetilstand for remskive a

Nå skriver vi balansetilstanden for remskiven som det ikke er noe annet enn summen av all kraften som virker på remskiven, må være ugyldig.

Å skille komponentene X og Y fra kreftene og legge til (vektorial) Følgende par av skalarligninger oppnås:

Kan tjene deg: Titan (satellitt)

F_TILX - T = 0; F_TILOG - T = 0

Disse ligningene fører til følgende likhet: f_Øks = F_ÅH = T.

Derfor har den radielle belastningen størrelse gitt av:

F_TIL = (T² + t²)^1/2 = 2^1/2∙ t = 1,41 ∙ t = 848,5 n. 45 ° retning. 

Balansetilstand for remskive B

Tilsvarende skriver vi likevektstilstanden for remskive B. For komponent x har du: f_BX + T + t ∙ cos45 ° = 0

Og for komponenten y: f_BOG + T ∙ Sen45 ° = 0

Dermed:

F_Bx = - t (1+2^-1/2) og f_Av = -T ∙ 2^-1/2

Det vil si at størrelsen på den radielle belastningen på remskiv B er:

F_B = ((1+2^-1/2) ² + 2^-1)^1/2∙ T = 1,85 ∙ T = 1108,66 N og adressen er 135 °.

Referanser

1. Beer F, Johnston E, DeWolf J, Mazurek, D. Materialmekanikk. Femte utgave. 2010. Mc Graw Hill. 1-130.
2. Gere J, Goodno, B. Materialmekanikk. Åttende utgave. Cengage Learning. 4-220.
3. Giancoli, d. 2006. Fysikk: Prinsipper med applikasjoner. 6^Tth Ed. Prentice Hall. 238-242.
4. Hibbeler R. Materialmekanikk. Åttende utgave. Prentice Hall. 2011. 3-60.
5. Valera Negrete, J. 2005. Generelle fysikknotater. Unam. 87-98.