Inelastiske sammenstøt i en dimensjon og eksempler

De Uelastiske sjokk eller uelastiske kollisjoner er et kort og intenst samspill mellom to objekter der bevegelsesmengden er bevart, men ikke den kinetiske energien, hvorav en prosentandel blir omgjort til en annen type energi.

Sjokk eller kollisjoner er hyppige i naturen. Subatomiske partikler kolliderer i veldig høye hastigheter, mens mange idretter og spill består av kontinuerlige kollisjoner. Til og med galakser er i stand til å kollidere.

Figur 1. Testbilkollisjon. Kilde: Pixabay

Egentlig er bevegelsesmengden bevart i alle typer kollisjon, så lenge partiklene kolliderte av et isolert system. Så i denne forstand er det ikke noe problem. Nå har objekter kinetisk energi assosiert med bevegelsen de har. Hva kan skje med den energien når du krasjer?

De interne kreftene som finner sted under sammenstøtet mellom gjenstandene er intense. Når det anføres at kinetisk energi ikke er bevart, betyr det at den blir omgjort til andre typer energi: for eksempel i lydenergi (en enhetskollisjon har en særegen lyd).

Flere bruksmuligheter for kinetisk energi: varme etter friksjon, og selvfølgelig den uunngåelige deformasjonen som ble lidd av gjenstander når de kolliderer, for eksempel billegemer i figuren over.

[TOC]

Eksempler på uelastiske kollisjoner 

- To masser av plastin som kolliderer og møtes sammen, og beveger seg som ett stykke etter krasjet.

- En gummikule som spretter mot en vegg eller gulv. Ballen deformeres når du påvirker overflaten.

Ikke all kinetisk energi transformeres til andre typer energi, bortsett fra i få unntak. Objekter kan holde seg med en viss mengde av denne energien. Senere får vi se hvordan du beregner prosentandelen.

Når brikkene som kolliderer er koblet sammen, kalles kollisjonen perfekt uelastisk, og begge ender vanligvis opp med å bevege seg sammen.

Perfekt uelastiske kollisjoner i en dimensjon

Kollisjonen av figuren viser to gjenstander av forskjellige masser m₁ og m₂, Flytter til hverandre med hastigheter v_i1 og v_I2 henholdsvis. Alt skjer på horisontalt, det vil si at det er en kollisjon i en dimensjon, det enkleste å studere.

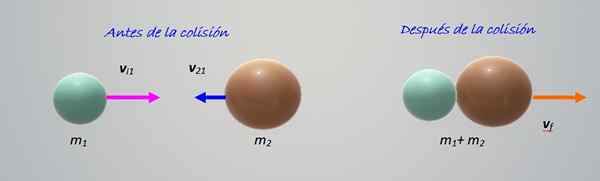Figur 2. Kollisjon mellom to partikler med forskjellige masser. Kilde: Selvlaget.

Objektene kolliderer og blir deretter forent og beveger seg til høyre. Det er en perfekt uelastisk kollisjon, så det er nok at vi holder bevegelsesmengden:

P_enten = P_F

Bevegelsesmengden er en vektor hvis enheter er n.s. I den beskrevne situasjonen kan vektornotasjonen dispenseres med når det er kollisjoner i en dimensjon:

Det kan tjene deg: enkle fysikkeksperimenter (primær-universitet)

Mv_enten = mv_F

Mengden av bevegelsen av systemet er vektorsummen for bevegelsesmengden til hver partikkel.

m₁ v_i1  + m₂ v_I2 = (m₁ + m₂) v_F

Den endelige hastigheten er gitt av:

v_F = (m₁ v_i1  + m₂ v_I2)/ (M₁ + m₂)

Restitusjonskoeffisient

Det er et beløp som kan indikere hvor elastisk er en kollisjon. Det handler om Restitusjonskoeffisient, som er definert som det negative forholdet mellom den relative hastigheten til partiklene etter krasjet og den relative hastigheten før krasjet.

La deg₁ og du₂ De respektive hastighetene til partiklene innledningsvis. Og være v₁ og v₂ de respektive slutthastighetene. Matematisk kan restitusjonskoeffisienten uttrykkes som følger:

Restitusjonskoeffisienten er en ekstra mengde, siden det er forholdet mellom hastigheter. Men informasjonen som er gitt er veldig interessant:

- Hvis ε = 0 tilsvarer å si at v₂ = v₁. Det betyr at de endelige hastighetene er de samme og at sammenstøtet er uelastisk, som beskrevet i forrige avsnitt.

- Når ε = 1 betyr at relativ hastighet både før og etter krasjet ikke endres, i dette tilfellet er sammenstøtet elastisk.

- Og hvis 0 < ε < 1 parte de la energía cinética de la colisión se transforma en alguna otra de las energías mencionadas anteriormente.

Hvordan bestemme restitusjonskoeffisienten?

Restitusjonskoeffisienten avhenger av klassen av materialer som er involvert i kollisjonen. En veldig interessant test for å bestemme hvordan elastisk er et materiale for å lage baller er å slippe ballen på en fast overflate og måle reboundhøyden.

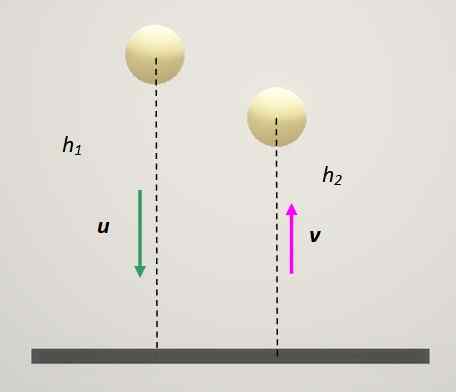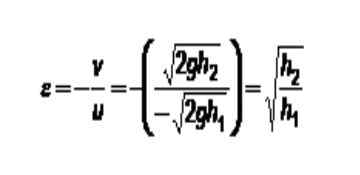
Figur 3. Metode for å bestemme restitusjonskoeffisienten. Kilde: Selvlaget.

I dette tilfellet har den faste platen alltid hastighet 0. Hvis denne indeksen 1 er tilordnet dette og ballen er: Indeks 2 gjenstår:

Den opprinnelige hastigheten avhenger av høyden h₁ hvorfra han droppet:

Det negative tegnet indikerer retning nedover. Og den endelige hastigheten er relatert til maksimal høyde h₂ som når i rebound:

Erstatte i restitusjonskoeffisienten du har:

Eksplosjoner

I begynnelsen har det blitt antydet at all kinetisk energi kan transformeres ved å flytte til andre typer energi. Tross alt blir ikke energi ødelagt. Er det mulig at gjenstander som fulgte med bevegelse kolliderer og slå sammen og danne et enkelt objekt som plutselig er i ro? Dette er ikke så enkelt å forestille seg.

Det kan tjene deg: Dynamikk: Historie, hvilke studier, lover og teorier

La oss imidlertid forestille oss hva som skjer bakover, som i en film sett i baksiden. Da ble objektet opprinnelig hvile og eksploderer deretter fragmentering i flere deler. Denne situasjonen er helt mulig: det er en eksplosjon.

Slik at en eksplosjon kan tenkes å være en perfekt uelastisk kollisjon sett bakover i tid. Bevegelsesmengden er også bevart, og kan bekrefte at:

P_enten = S_F

Løste eksempler

-Oppgave 1

Det er kjent fra målinger at stålrestitusjonskoeffisienten er 0.90. En stålkule slippes fra 7 m høy på en fast plate. Regne ut:

a) til hvilken høyde vil sprette.

b) Hvor lang tid tar det mellom den første kontakten med overflaten og den andre.

Løsning

a) Ligningen som tidligere ble trukket ut i seksjonen om bestemmelse av restitusjonskoeffisienten, brukes:

Høyde rydder h₂:

0.90² . 7 m = 5.67 m

b) å heve 5.67 meter en hastighet gitt av:

Hvor fra:

Og tiden det tar å nå denne høyden er:

t _Maks = v_enten/ g = (10.54/9.8 s) = 1.08 s.

Tiden det tar å returnere er den samme, derfor den totale tiden for å laste opp de 5.67 meter og tilbake til utgangspunktet er det dobbelte av maksimal tid:

t_flygning = 2.15 s.

-Oppgave 2

Figuren viser en treblokk med masse m hengende i resten av lengder av lengde l som pendel. Dette kalles den ballistiske pendelen og tjener til å måle hastigheten v for inngangen en masse av masse m. Jo høyere hastighet som kulen påvirker blokken med, i en høyere høyde h, vil bygges.

Bildekulen er innebygd i blokken, derfor er det et helt uelastisk sjokk.

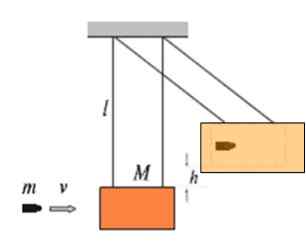Figur 4. Den ballistiske pendelen.

Anta at en 9 9.72 g påvirkning mot masseblokken 4.60 kg, så stiger settet til 16.8 cm av likevektsposisjonen. Hva er hastigheten v av kulen?

Løsning

Under kollisjonen er bevegelsesmengden bevart og eller_F Det er hastigheten på settet, når kulen har innebygd i blokken:

P_enten = S_F

Blokken hviler opprinnelig, mens kulen er rettet mot målet med hastighet v:

m.v + m.0 = (m + m) u_F

 

Det er ikke kjent eller_F Til og med, men etter kollisjon bevares mekanisk energi, dette er summen av gravitasjonspotensial energi og kinetisk energi k:

Kan tjene deg: Summen av vektorer: grafisk metode, eksempler, løste øvelser

Innledende mekanisk energi = endelig mekanisk energi

OG_Mo = E_Mf

ELLER_enten + K_enten = U_F + K_F

Gravitasjonspotensiell energi avhenger av høyden som settet når. For likevektsposisjonen er den opprinnelige høyden den som er tatt som et referansenivå, derfor:

ELLER_enten = 0

Takket være kulen har settet kinetisk energi K_enten, som blir gravitasjonspotensiell energi når settet når sin maksimale høyde h. Kinetisk energi er gitt av:

K = ½ mv²

Opprinnelig er kinetisk energi:

K_enten = (1/2) (m+m) u_F²

Husk at kulen og blokken danner et enkelt masseobjekt M+ m. Gravitasjonspotensialenergien når de har nådd i sin maksimale høyde er:

ELLER_F = (M + M) GH

Derfor:

K_enten = U_F

(1/2) (m+m) u_F² = (M + M) GH

Nå erstattes dette resultatet i uttrykk for v som ryddet i begynnelsen, fra bevaring av bevegelsesmengden:

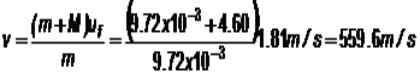
-Øvelse 3

Figurens objekt eksploderer i tre fragmenter: to av like masse m og en større masse 2m. Figuren indikerer hastighetene til hvert fragment etter eksplosjonen. Hva var objektets opprinnelige mål?

Figur 5. Steinen som eksploderer i 3 fragmenter. Kilde: Selvlaget.

Løsning

Dette problemet krever bruk av to koordinater: x og og, Fordi to av fragmentene har vertikale hastigheter, mens de resterende har horisontal hastighet.

Den totale massen til objektet er summen av massen av alle fragmenter:

M = m + m + 2m = 4m

Bevegelsesmengden er bevart både på x -aksen og på Y -aksen, den foreslås separat:

1. 4m. eller_x= m v₃
2. 4m. eller_og = m. 2V₁ - 2m. v₁

Merk at det store fragmentet beveger seg ned med V1 -hastighet, for å påpeke dette faktum at et negativt tegn er plassert.

Fra den andre ligningen følger den umiddelbart at eller_og = 0, Og den første er tydelig UX umiddelbart:

Det første målet med objektet var u_enten = u_x = v₃/4.

Referanser

1. Giancoli, d.  2006. Fysikk: Prinsipper med applikasjoner. 6^th. Ed Prentice Hall. 175-181
2. Rex, a. 2011. Fundamentals of Physics. Pearson. 135-155.
3. Serway, r., Vulle, c. 2011. Fundamentals of Physics. 9^na Cengage Learning. 172 -182
4. Tipler, s. (2006) Fysikk for vitenskap og teknologi. 5. utg. Volum 1. Redaksjon tilbake. 217-238
5. Tippens, p. 2011. Fysikk: konsepter og applikasjoner. 7. utgave. MacGraw Hill. 185 -195