Hvordan få prosentandelen? Eksempler og øvelser

Kan Få en prosentandel Med flere metoder. Du kan raskt beregne 10% av et hvilket. For eksempel er 10% av 100 10; 10% av 1000 er 100.

Hvis du vil beregne mer komplekse prosenter som 36% av 25 eller 250% av 20, er andre metoder nødvendig. For tilfeller der 10% -systemet ikke er aktuelt, kan følgende metodologier tas i betraktning.

Figur 1. Rabatter med forskjellige prosentandeler. Hvor mye sparer vi hverandre?. Kilde: Pixabay.

Begrepet prosentandel betyr en viss del av hvert hundre og refererer til den aritmetiske operasjonen som utføres for å finne nevnte del. For eksempel er 20% ("tjue prosent") lest i pesos, det betyr at 20 pesos er diskontert for hver 100 pesos.

Prosentandelen tjener til å beregne hvilken del av totalen som representerer et beløp. I dette tilfellet tas totalen til skalaen på 100 og prosentandelen informerer hvor mye, basert på de 100, er den delen som skal beregnes.

La oss se hvordan det gjøres med disse eksemplene. For det første gjør vi det i form av en brøkdel:

• 20% = 20/100
• 5% = 5 /100
• 0,7% = 0,7 / 100
• 100% = 100 /100

Merk at 100% er lik 1. Men prosentene kan også skrives desimal:

• 20% = 0,20
• 5% = 0,05
• 0,7% = 0,007
• 100% = 1,0

Når prosentandelen av et visst antall er uttrykt, enkelt Komma beveger seg Av det nummer to steder til venstre. I prosentandelen, proporsjonalitetsregel:

20% er 20 av 100, derfor:

20% av 100 er 20, 20% av 200 er 40, 20% av 300 er 60, 20% av 50 er 10.

Generell regel for 20 % av ethvert beløp

20% av x er x *(20/100) = x *0,2 = 0,2 *x

Denne regelen kan lett utvide seg for å finne enhver annen prosentandel som er ønsket. La oss se hvordan i følgende avsnitt.

Trening løst med formel for å beregne n% 

En formel for å oppsummere så snart som mulig og raskt beregne enhver prosentandel n er:

n % =(A * n)/100

For eksempel vil du beregne 25% av 400

Deretter n = 25 og A = 400, noe som resulterer i (400*25)/100 = 100

Eksempel

Hvilken prosentandel av 60 er 24?

Løsning

Det som blir bedt om tilsvarer å spørre hva som er n% av 60 som gir 24?

Vi foreslår den generelle formelen:

60 * n / 100 = 24

Vi klarer n Med denne prosedyren:

-De 100 som deler seg inn i medlem IZiédo Av likhet, gå til medlemmet Ikke sant multiplisere. 

-Og de 60 som multipliserer i medlemmet venstre Gå til medlemmet Ikke sant deling.

N = 24 *100/60 = 2400/60 = 240/6 = 6 *40/6 = 40

Det konkluderes med at 40% av 60 er 24.

Løst prosentvis beregningsøvelser 

Nedenfor er enkle øvelser for å begynne å øve på nevnte.

Det kan tjene deg: de 15 mest populære legendene og mytene

Oppgave 1

Finn 50% av 90.

Løsning

Her x = 90, n = 50 % og erstatt:

90 * 50% = 90 * (50/100) = 4500 /100 = 45 

Dette er ganske enkelt, fordi 50 % av ethvert beløp er halvparten av det beløpet og halvparten av 90 er 45.

Oppgave 2

Finn 30% av 90.

Løsning

90 * 30% = 90 * (30/100) = 2700 /100 = 27

Prosentandelen øker

Det er hyppig i hverdagen å lytte til økningen i noe, for eksempel en økning i produksjonen, en lønnsøkning eller økningen av et produkt. Det kommer nesten alltid til uttrykk i prosentform.

For eksempel koster en viss produkt € 300, men led en økning på 30%. Vi spør oss selv: Hva er den nye produktprisen?

Den første er å beregne den delen som tilsvarer økningen. Ettersom økningen er 30 deler av 100, så er økningen i økningen, basert på den opprinnelige prisen på 300, tre ganger de 30 delene, det vil si 3*30 = 90.

Produktet økte € 90, så den nye sluttprisen vil være den som koster økningen før:

Ny pris = gammel pris + € 90 = € 390

Vi kan bygge en formel for beregning av prosentvis økning. Vi bruker bokstaver for å symbolisere priser, som dette:

-F er den endelige verdien

-Yo er startverdien og

-n er økningen i økning.

Med disse navnene vil den endelige verdien bli beregnet slik:

f = i + (i* n / 100)

Men hvordan Yo Det gjentas i begge termer, det kan tas som en vanlig faktorFor å få dette andre uttrykket, like gyldig:

F = i * (1 + n / 100)

La oss bekrefte med saken som allerede er løst, produktet som koster € 300 og økte 30%. Dermed sørger vi for at formelen fungerer bra:

Endelig pris = F = € 300 * (1 + 30/100) = € 300 * (1 + 0,3) = € 300 * 1,3 = € 390

Øvelse 3

En ansatt tjente € 1500, men ble forfremmet og lønnen hans hadde 20% økning. Hva er din nye lønn?

Løsning

La oss bruke formelen:

F = € 1500 * (1 + 20/100) = € 1500 * (1 + 0,2) = € 1500 * 1,2 = € 1800

Den nye ansattes lønn er € 1800.

Prosentandelen avtar

Når det gjelder reduksjoner, er formelen for beregning av den endelige verdien F av et visst startbeløp Yo som led en nedgang i n% er:

F = i * (1 - n / 100)

Det skal bemerkes at det positive tegnet (+) av formelen i forrige seksjon ble erstattet av et negativt tegn (-).

Figur 2. Prosentvis rabattvarsel. Kilde: Pixabay

Oppgave 4

Et produkt merket € 800, men fikk 15% rabatt. Hva er den nye produktprisen?

Løsning 4

Den endelige prisen i henhold til formelen er:

F = € 800 * (1 - 15/100) = € 800 * (1 - 0,15) = € 800 * (0,85) = € 680

Den endelige prisen med 15% rabatt er € 680, som representerer en besparelse på € 120.

Påfølgende prosenter

Det ser ut til når noe beløp lider en prosentvis variasjon og deretter blir brukt, også en prosentandel. For eksempel et produkt som har hatt to prosentvise rabatter på rad. Et annet eksempel er en ansatt som hadde to lønnsøkninger på rad.

Kan tjene deg: viktigere Yucatan økonomiske aktiviteter

- Påfølgende prosentandel øker

Løsningsbasen til disse tilfellene er den samme som de unike økningene, men det må tas i betraktning at den andre prosentvis økningen blir utført på den endelige verdien av den første økningen.

Anta at et produkt som steg først 10% og deretter 5%. Det er feil å si at det led en økning på 15%, det var faktisk mer enn denne prosentandelen.

Formlene for den endelige verdien vil gjelde slik:

-Først beregnes den endelige verdien av den første økningen på N1%

f1 = i + i * n1 / 100

-Og for å finne den endelige verdien av den andre økningen på N2%, blir den endelige verdien av F1 tatt som en startverdi. Derfor:

F2 = f1 + f1 * n2 /100 

Oppgave 5

En bok kostet opprinnelig € 55, men på grunn av dens suksess og høye etterspørsel, led den to påfølgende økninger på den opprinnelige prisen. Den første økningen var 10% og den andre av 20%. Hva er den endelige prisen på boka?

Løsning

-Første økning:

F1 = € 55 * (1 + 10/100) = € 55 * 1,1 = € 60,5

-Andre økning

F2 = € 60,5 * (1 + 20/100) = € 60,5 * 1,2 = € 72,6

Den endelige prisen er € 72,6.

Oppgave 6

Med henvisning til forrige øvelse. De to øker på rad: til hvilken prosentandel av en unik økning i forhold til den opprinnelige bokprisen korresponderer?

Løsning

Hvis vi kaller N% til prosentandelen av unik økning, er formelen som relaterer denne unike prosentvise økningen til den opprinnelige verdien og den endelige verdien:

F2 = i *(1 + n / 100) 

Det er å si:

€ 72,6 = € 55 + 55 € * (n / 100)

Rydde økningen i økning n% = (n /100), har vi:

(N / 100) = (€ 72,6 - € 55) / 55 € = 17.€ 6 / € 55 = 0,32

Derfor:

N = 0,32 * 100 = 32

Til prisen på boka ble det brukt en total prosentvis økning på 32%. Merk at denne økningen er større enn summen av de to påfølgende prosentandelen øker.

- Påfølgende prosentvise rabatter

Ideen ligner på den påfølgende prosentvise økningen. Den andre prosentvise rabatten må alltid brukes på den endelige verdien av den første rabatten, la oss se på et eksempel:

Oppgave 7

En 10% rabatt etterfulgt av en ny rabatt på 20% på et objekt, som unik prosentvis rabatt er det tilsvarende?

Løsning

-Første rabatt:

F1 = i - i * n1 / 100  

-Andre rabatt

F2 = f1 - f1 * n2 / 100

Å erstatte den første ligningen i den andre gjenstår:

f2 = (i - i * n1 / 100) - (i - i * n1 / 100) * n2 / 100

Utvikle dette uttrykket får vi:

F2 = I - I* N1 / 100 - I* N2 / 100 + I* (N1 / 100) (N2 / 100) 

Tegne vanlig faktor Yo:

F2 = I * (1- N1% - N2% + N1% * N2%)

Til slutt erstattes prosentene som er angitt i spørsmålet:

F2 = I * (1 - 10% - 20% + 10% * 20%) = I * (1 - 0,1 - 0,2 + 0,1 * 0,2)

f2 = i * (1 - 0,3 + 0,02) = i * (0,72) = I * (1 - 0.28) = i * (1 - 100/100) = I * (1 - 28%)

Med andre ord, påfølgende rabatter på 10% og 20% ​​tilsvarer en unik rabatt på 28%.

Avanserte øvelser

La oss prøve disse øvelsene bare når ideene til de tidligere har vært klare nok.

Det kan tjene deg: enkle og vakre geografiseksler, omslag, bilder

Oppgave 8

Basen til en trekant måler 10 cm og høyde 6 cm. Hvis grunnlengden synker med 10%. I hvilken prosentandel skal høyden økes slik at trekantområdet ikke endres?

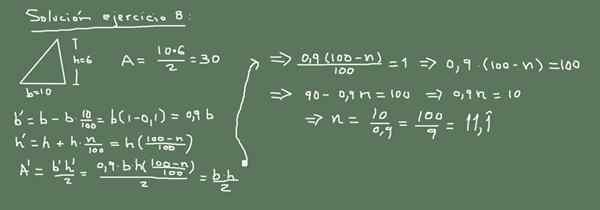Figur 3. Alternativ løsning på trening 8. Utarbeidet av f. Zapata.

Løsning 8

Det opprinnelige trekantområdet er:

A = (10 cm * 6cm) / 2 = 30 cm²

Nå, hvis basen synker med 10%, er den nye verdien:

Ny base = 10 - (10/100) x 10 = 9 cm.

Den nye høydeverdien vil være x, og det opprinnelige området må holdes uendret, slik at:

(9cm * x) /2 = 30 cm²

Da blir verdien av x fjernet som:

X = 60 cm² / 9 cm = (20/3) cm = 6,666 cm

Som betyr en økning på 0,666 sammenlignet med den opprinnelige verdien. La oss nå se hvilken prosentandel av dette som representerer:

6,666 = 6 + (6 * n/100) 

6,666 -6 = 6 * n/100

0.666 = 6 * N/100

N/100 = 0.111

N = 11.1

Svaret er: høyden må økes med 11,1% for at trekantområdet skal forbli den samme.

Øvelse 9

Hvis lønnen økes med 20%, men så skattemeldinger 5%, hva er den virkelige økningen som arbeideren mottar?

Løsning 

Først beregner vi økningen på N1%:

f1 = i + i * n1 / 100

Så bruker vi N2%rabatt:

F2 = f1 - f1 * n2 / 100

Den første ligningen erstattes i den andre:

f2 = i + i * n1 / 100 - (i + i * n1 / 100) * n2 / 100

Det forrige uttrykket utvikler seg:

f2 = i + i * n1 / 100 - i * n2 / 100 - i * (n1 / 100) * (n2 / 100)

Endelig fjernes den Yo Vanlig faktor og verdiene til n1 = 20 og n2 = 5 som vises i uttalelsen erstattes:

F2 = I (1 + 0,2 - 0,05 - 0,2* 0,05) = I* (1 + 7/50) = I* (1 + 14/100) = I* (1 + 14%)

Arbeideren fikk en netto økning på 14%.

Øvelse 10

Bestem hva som er mest praktisk mellom disse to alternativene:

i) skaffe t -skjorter med 32 % rabatt hver.

Ii) Kjøp 3 t -skjorter for prisen på 2.

Løsning 

Vi analyserer hvert alternativ hver for seg og velger deretter det mest økonomiske:

i) La X være den nåværende prisen på en skjorte, en 32 % rabatt representerer en endelig pris på XF:

Xf = x - (32/100) x = x - 0.32x = 0.68x

Å kjøpe 3 skjorter betyr for eksempel å bruke 3 x 0.68 x = 2.04x

ii) Hvis x er prisen på en skjorte, for 3 skjorter vil du ganske enkelt betale 2x.

Anta at en skjorte er verdt 6 euro, med 32 % rabatt ville det være verdt 4.08 euro. Kjøp 1 T -skjorte er ikke et gyldig alternativ i 3 × 2 -tilbudet. Så hvis du bare vil kjøpe 1 skjorte, er rabatten å foretrekke.

Men hvis det du vil er å kjøpe for dusinvis, er 3 × 2 -tilbudet bare litt billigere. For eksempel ville 6 t -skjorter med rabatten gå ut i 24.48 euro, mens de med 3 × 2 -tilbudet ville koste 24 euro

Referanser

1. Enkelt klasserom. Prosenten. Hentet fra: Klasserom.com
2. Baldor a. 2006. Praktisk teoretisk aritmetikk. Kulturelle utgaver.
3. Educa Kids. Hvordan lære å beregne prosenter. Gjenopprettet fra: Educapeques.com
4. Gutiérrez, g. Finansielle matematikknotater. Gjenopprettet fra: CSH.Izt.Uam.MX
5. Smarte flått. Prosent: Hva er og hvordan beregnes. Gjenopprettet fra: Smartick.er