Bestemmelseskoeffisientformler, beregning, tolkning, eksempler

Han Bestemmelseskoeffisient Det er et tall mellom 0 og 1 som representerer brøkdelen av punkter (x, y) som følger justeringslinjen ved regresjon av et datasett med to variabler.

Det er også kjent som justering godhet og er betegnet med r². For å beregne det, tas kvotienten mellom variansen til ŷi -dataene estimert av regresjonsmodellen og variansen til YI -dataene som tilsvarer hver XI av dataene.

R² = Sŷ / SY

Figur 1. Korrelasjonskoeffisient for fire datapar. Kilde: f. Zapata.

Hvis 100% av dataene er på regresjonsfunksjonslinjen, vil bestemmelseskoeffisienten være 1.

Tvert imot, hvis for et datasett og en viss justeringsfunksjon, R -koeffisienten R² Det viser seg å være lik 0.5, da kan det sies at justeringen er tilfredsstillende eller god på 50%. 

Tilsvarende når regresjonsmodellen kaster verdier av r² Mindre enn 0.5, dette indikerer at den valgte justeringsfunksjonen ikke tilpasser seg tilfredsstillende til dataene, derfor nødvendig for å se etter en annen justeringsfunksjon.

Og når samvariasjon eller korrelasjonskoeffisient Det har en tendens til null, da er ikke variablene x og y fra dataene relatert, og derfor r² vil også ha en tendens til null.

[TOC]

Hvordan beregne bestemmelseskoeffisienten?

I forrige seksjon ble det sagt at bestemmelseskoeffisienten beregnes ved å finne kvotienten mellom variansene:

-Estimert av regresjonsfunksjonen til variabelen og 

-YI -variabelen som tilsvarer hver av XI -variabelen. 

I matematisk form forblir det slik:

R² = Sŷ / SY

Fra denne formelen følger det at r² representerer andelen av variansen forklart av regresjonsmodellen. Alternativt kan R beregnes² Gjennom følgende formel, tilsvarer helt den forrige:

R² = 1 - (Sε / SY)

Hvor Sε representerer variansen til avfallet εi = ŷi - yi, mens SY er variansen til datasettet til dataene til dataene. For å bestemme ŷi blir regresjonsfunksjonen brukt, noe som betyr å bekrefte at ŷi = F (xi).

Det kan tjene deg: brøkdel tilsvarer 3/5 (løsning og forklaring)

Variansen til Yi -datasettet, med I fra 1 til N, beregnes på denne måten:

Sy = [σ (yi -)² ) / (N-1)]

Og fortsett deretter på en lignende måte for Sŷ eller for Sε.

Illustrerende sak

Som å vise detaljene om måten beregningen av Bestemmelseskoeffisient Vi tar følgende sett med fire par data: 

(X, y): (1, 1); (23); (3, 6) og (4, 7).

En lineær regresjonsjustering foreslås for dette datasettet oppnådd ved metoden for kvadratiske minimumsnivåer:

f (x) = 2.1 x - 1 

Ved å bruke denne justeringsfunksjonen oppnås jevnaldrende:

(X, ŷ): (1, 1.1); (23.2); (3, 5.3) og (4, 7.4).

Deretter beregner vi det aritmetiske gjennomsnittet for x og y:

= (1 + 2 + 3 + 4) / 4 = 2.5

= (1 + 3 + 6 + 7) / 4 = 4.25

Varians SY

SY = [(1 - 4.25)² + (3. 4.25)² + (6 - 4.25)² +.. ... .(7 - 4.25)²] / (4-1) =

= [-3.25)²+ (-1.25)² + (1.75)² + (2.75)²) / (3)] = 7.583

Varians sŷ

Sŷ = [(1.1 - 4.25)² + (3.2 - 4.25)² + (5.3. 4.25)² +.. ... .(7.4 - 4.25)²] / (4-1) =

= [-3.25)² + (-1.25)² + (1.75)² + (2.75)²) / (3)] = 7.35

Bestemmelseskoeffisient r²

R² = Sŷ / SY = 7.35/7.58 = 0.97

Tolkning

Bestemmelseskoeffisienten for det illustrerende tilfellet som ble vurdert i forrige segment, viste seg å være 0.98. Det vil si at den lineære justeringen gjennom funksjonen:

 f (x) = 2.1x - 1

Det er 98% pålitelig å forklare dataene de ble oppnådd med minimum kvadratmetode. 

I tillegg til bestemmelseskoeffisienten, er det Lineær korrelasjonskoeffisient eller også kjent som Pearson -koeffisienten. Denne koeffisienten, betegnet som r, Det beregnes ved følgende forhold:

R = sxy / (sx sy)

Her representerer telleren samvariasjonen mellom variablene x og y, mens nevneren er produktet av standardavviket for variabel x og standardavviket for variabelen og.

Pearsons koeffisient kan ta verdier mellom -1 og +1. Når denne koeffisienten har en tendens til +1, er det direkte lineær korrelasjon mellom x og y. Hvis det i stedet har en tendens til -1, er det lineær korrelasjon, men når X vokser og avtar. Endelig er det nær 0 det er ingen sammenheng mellom de to variablene.

Kan tjene deg: grupperte data: eksempler og trening løst

Det skal bemerkes at bestemmelseskoeffisienten sammenfaller med kvadratet av Pearson -koeffisienten, bare når den første er blitt beregnet basert på en lineær justering, men denne likheten er ikke gyldig for andre ikke -lineære justeringer.

Eksempler

- Eksempel 1

En gruppe elever på videregående skoler har til hensikt å bestemme en empirisk lov for en pendelperiode som en funksjon av dens lengde. For å oppnå dette målet, lager de en serie målinger der de måler tidspunktet for en pendelsvingning i forskjellige lengder som oppnår følgende verdier:

Lengde (m)	Periode (er)
0.1	0.6
0.4	1.31
0.7	1.78
1	1.93
1.3	2.19
1.6	2.66
1.9	2.77
3	3.62

Det blir bedt om å lage en datadispersjonsgraf og gjøre en lineær justering ved regresjon. I tillegg viser regresjonsligningen og dens bestemmelseskoeffisient.

Løsning

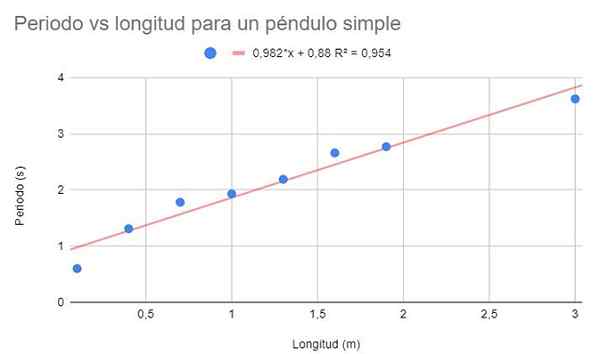Figur 2. Grafisk løsning av trening 1. Kilde: f. Zapata.

En ganske høy bestemmelseskoeffisient (95%) kan observeres, så det kan tenkes at den lineære justeringen er optimal. Imidlertid, hvis punktene blir observert sammen, ser det ut til at de har en tendens til å krumme ned. Denne detaljene er ikke tenkt i den lineære modellen.

- Eksempel 2

For de samme dataene i eksempel 1, lag et databrattdiagram. I denne anledningen, i motsetning til eksempel 1, blir det bedt om å gjøre en regresjonsjustering gjennom en potensiell funksjon.

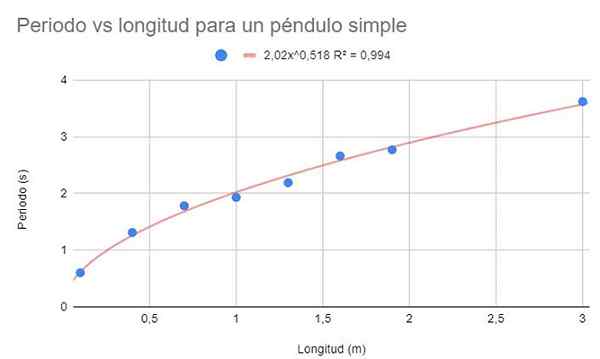Figur 3. Grafisk løsning av trening 2. Kilde: f. Zapata.

Vis også justeringsfunksjonen og dens R -bestemmelseskoeffisient².

Løsning

Den potensielle funksjonen er av formen f (x) = øks^B, hvor a og b er konstante som bestemmes ved minimum kvadratmetode.

Den forrige figuren viser den potensielle funksjonen og dens parametere, så vel som bestemmelseskoeffisienten med en veldig høy verdi på 99%. Merk at dataene følger krumningen av trendlinjen.

Kan tjene deg: Additive Principle

- Eksempel 3

Med de samme dataene fra eksempel 1 og eksempel 2, lag en annen grad av polynomjustering. Vis grafen, justeringspolynomet og bestemmelseskoeffisienten r² korrespondent.

Løsning

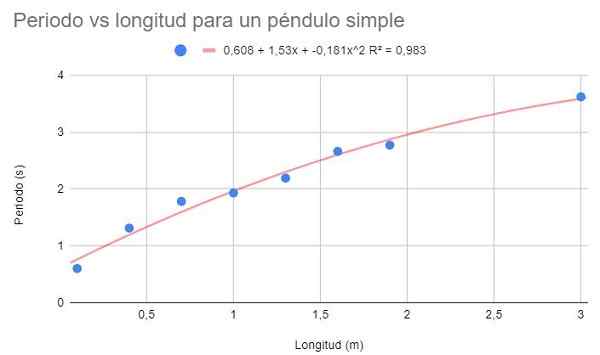Figur 4. Grafisk øvelse 3 Graf. Kilde: f. Zapata.

Med andre grads polynomjustering kan en trendlinje sees som passer godt til krumningen av dataene. På samme måte er bestemmelseskoeffisienten over den lineære justeringen og under den potensielle justeringen.

Justeringssammenligning

Av de tre justeringene som er vist, er den med en høyere bestemmelseskoeffisient den potensielle justeringen (eksempel 2).

Den potensielle justeringen sammenfaller med den fysiske teorien om pendelen, som, som det er kjent, slår fast at perioden med en pendel er proporsjonal med kvadratroten av dens lengde, og er konstanten av proporsjonalitet 2π /√g der g er akselerasjonen av tyngdekraften.

Denne typen potensielle justeringer har ikke bare den høyeste bestemmelseskoeffisienten, men eksponenten og proporsjonalitetskonstanten sammenfaller med den fysiske modellen. 

Konklusjoner

-Regresjonsjusteringen bestemmer parametrene til funksjonen som tar sikte på å forklare dataene gjennom minimum kvadratmetoden. Denne metoden består i å minimere summen av den kvadratiske forskjellen mellom verdien og justeringen og YI -verdien til dataene for XI -verdiene til dataene. På denne måten bestemmes parametrene for justeringsfunksjonen.

-Som vi har sett, er den vanligste justeringsfunksjonen linjen, men den er ikke den eneste, siden justeringene også kan være polynom, potensial, eksponentiell, logaritmer og andre. 

-I alle fall avhenger bestemmelseskoeffisienten av dataene og justeringstypen og er et indikasjon på godheten til den anvendte justeringen.

-Til slutt indikerer bestemmelseskoeffisienten prosentandelen av total variasjon mellom verdien og dataene med hensyn til ŷ -verdien av justeringen for x gitt.

Referanser

1. González c. Generell statistikk. Gjenopprettet fra: Tarwi.La Molina.Edu.PE
2. IACS. Aragonese Institute of Health Sciences. Hentet fra: ICS-Aagon.com
3. Salazar c. og Castillo s. Grunnleggende statistikkprinsipper. (2018). Hentet fra: DSPACE.Uce.Edu.Ec
4. Superprof. Bestemmelseskoeffisient. Gjenopprettet fra: Superprof.er
5. USAC. Beskrivende statistikkhåndbok. (2011). Gjenopprettet fra: Statistikk.Ingeniørfag.USAC.Edu.Gt.
6. Wikipedia. Bestemmelseskoeffisient. Gjenopprettet fra: er.Wikipedia.com.