Tukey -test i det som er, mester, trening løst

De Tukey -test Det er en metode som tar sikte på å sammenligne individuelle gjennomsnitt fra en variansanalyse av flere prøver under.

Testen, presentert i 1949 av John.W. Tukey, tillater å skille om resultatene som er oppnådd er betydelig forskjellige eller ikke. Det er også kjent som Tukey ærlig betydelig forskjellstest (Tukey's HSD -test for sitt forkortelse på engelsk).

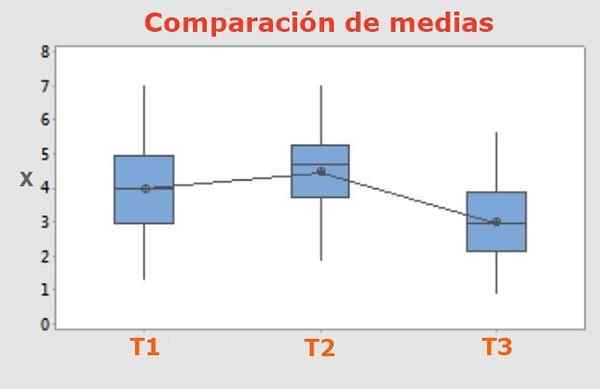
Figur 1. Tukey -testen gjør det mulig å skille om forskjellene i resultat mellom tre eller flere forskjellige behandlinger anvendt på tre eller flere grupper med like store egenskaper, har betydelige og ærlig forskjellige gjennomsnittsverdier.

I eksperimenter der det sammenligner mellom tre eller flere forskjellige behandlinger som brukes på samme antall prøver, er det nødvendig å skille om resultatene er betydelig forskjellige eller ikke.

Det sies at et eksperiment er balansert når størrelsen på alle statistiske prøver er det samme i hver behandling. Når prøvetakingsstørrelsen er forskjellig for hver behandling, er det da et ikke -balansert eksperiment.

Noen ganger er det ikke nok med en variansanalyse (ANOVA) å vite om de i sammenligningen av forskjellige behandlinger (eller eksperimenter) brukes på flere prøver de oppfyller nullhypotesen (ho: "Alle behandlinger er de samme") eller tvert imot det Møter den alternative hypotesen (HA: "Minst en av behandlingene er annerledes").

Tukey -testen er ikke unik, det er mange flere bevis for å sammenligne eksempler på, men dette er et av de mest kjente og anvendte.

[TOC]

Comparator og Tukey -bord

I anvendelsen av denne testen beregnes en verdi W ringte Tukey Comparator hvis definisjon er som følger:

W = Q √ (MSE /R)

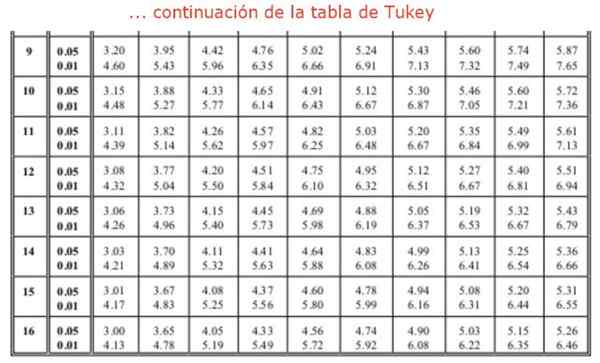
Hvor faktoren q Det er hentet fra en tabell (Tukey -tabell), som består av verdier av verdier q For forskjellige antall behandlinger eller eksperimenter. Kolonnene indikerer faktorverdien q For forskjellige frihetsgrader. Normalt har de tilgjengelige tabellene relative midler til 0.05 og 0.01.

Kan tjene deg: i påvente av en linje: formel og ligninger, representasjon, eksempler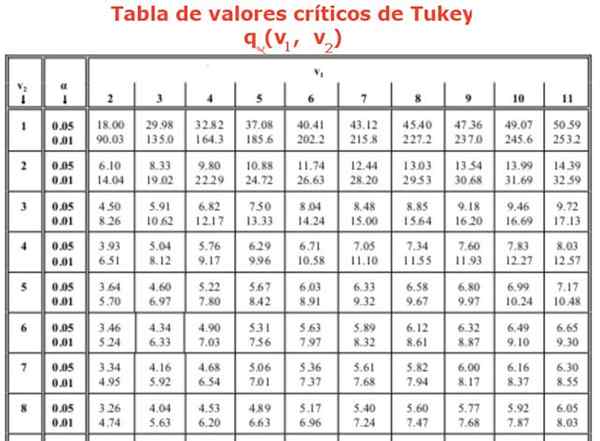

I denne formelen vises MSE -faktoren innenfor kvadratroten (gjennomsnittlig kvadrat for feilen) delt på R, noe som indikerer antall repetisjoner. MSE er et tall som normalt oppnås fra en analyse av avvik (ANOVA).

Når forskjellen mellom to gjennomsnittsverdier overstiger verdien W (Tukey Comparator), da konkluderes det med at dette er forskjellige gjennomsnitt, men hvis forskjellen er mindre enn Tukey -nummeret, er det to prøver med statistisk identisk gjennomsnittsverdi.

W -tallet er også kjent som HSD -nummer (ærlig betydelig forskjell).

Dette eneste komparatornummeret kan brukes hvis antall prøver som brukes på testen av hver behandling er det samme i hver av dem.

Ubalanserte eksperimenter

Når størrelsen på prøvene av en eller annen grunn er forskjellig i hver behandling for å sammenligne, er prosedyren beskrevet ovenfor seg litt og er kjent som Tukey-Kramer Test.

Nå er det oppnådd et tall W komparator for hvert par behandling i, j:

w (i, j) = q √ (½ mse /(ri +rj))

I denne formelen er faktoren som er oppnådd fra Tukey -tabellen. Nevnte faktor som avhenger av antall behandlinger og grad av feilfrihet. r_Yo Det er antall repetisjoner i behandlingen i, mens r_J Det er antall repetisjoner i J -behandlingen.

Eksempel sak

En kaninoppdretter ønsker å gjøre en pålitelig statistisk studie som indikerer å vite hvilke av de fire kaninfetende matmerkene som er mest effektive. For studien danner den fire grupper med seks og en halv kaniner som til den tid hadde de samme matforholdene.

Fra eksperimentet til den første gruppen kalles det A1 fordi den vil mate av maten til merkevare 1, på samme måte med gruppe A2, A3 og A4. Det lages en tabell der vektøkningen (i kilo) av hvert eksemplar etter en måned med mat med de forskjellige matmerkene er registrert, og oppnår følgende resultater: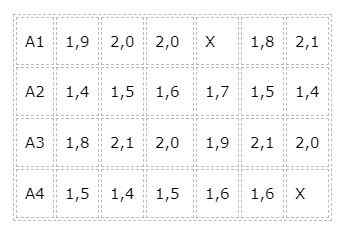Selv om det begynte med et balansert eksperiment, i den forstand at antallet kaniner som behandlingen ville bli brukt til var det samme, kunne eksperimentet ikke være ferdig på denne måten.

Kan tjene deg: negativ homotecia

Årsakene var at i gruppe A1 og A4 dødsfall skjedde på grunn av årsaker som ikke kan tilskrives mat, siden en av kaninene ble hakket av et insekt og i det andre tilfellet var døden sikkert årsaken til en medfødt defekt. Slik at gruppene er ubalanserte og da er det nødvendig å bruke Tukey-Kramer-testen.

Trening løst

For ikke å utvide beregningene for mye, vil et tilfelle av balansert eksperiment bli tatt som en øvelse løst. Følgende vil bli tatt som data:

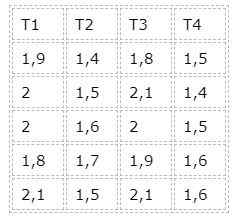
I dette tilfellet er det fire grupper som tilsvarer fire forskjellige behandlinger. Vi observerer imidlertid at alle grupper har samme antall data, så det er da en balansert sak.

For å utføre ANOVA -analysen, er verktøyet som er integrert i regnearket til LibreOffice. Andre regneark som som utmerke De har dette verktøyet for dataanalyse innarbeidet. Nedenfor er en sammendragstabell som har resultert etter variansanalysen (ANOVA):

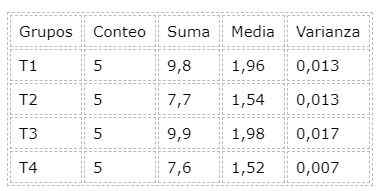
Fra variansanalyse er det også verdien P, som for eksempel er 2.24e-6 godt under 0.05 av nivået av betydning, som direkte fører til å avvise nullhypotesen: alle behandlinger er like. 

Det er, blant behandlingene har noen forskjellige gjennomsnittsverdier, men du må vite hva som er det viktige og ærlig annerledes (HSD) fra det statistiske synspunktet ved hjelp av Tukey -test.

For å finne tallet w eller som HSD -nummeret også er kjent, krever vi gjennomsnittlig kvadrat for MSE -feilen. Fra ANOVA -analyse oppnås det at summen av firkanter i gruppene er SS = 0,2; Og antallet frihetsgrader i gruppene er df = 16 med disse dataene vi kan finne MSE:

Kan tjene deg: papomudas

MSE = SS/df = 0,2/16 = 0,0125

Det er også påkrevd å finne faktoren q av Tukey, ved hjelp av tabellen. Det er søkt i kolonne 4 som tilsvarer de 4 gruppene eller behandlingene for å sammenligne og rad 16, siden ANOVA -analysen viste 16 frihetsgrader i gruppene. Dette fører oss til en verdi av Q lik: Q = 4.33 tilsvarende 0,05 betydning eller 95% pålitelighet. Til slutt blir verdien for den "ærlig signifikante forskjellen" funnet:

W = hsd = Q √ (MSE /R) = 4,33 √ (0,0125 /5) = 0,2165

For å vite hva de ærlig forskjellige gruppene eller behandlingene er, må du vite gjennomsnittet av hver behandling:

Det er også nødvendig å vite forskjellene mellom gjennomsnittsverdiene for behandlingspar, som er vist i følgende tabell:

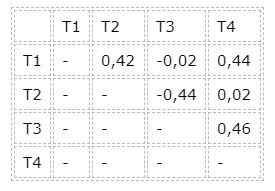T3- og T1 -grupper, så vel som grupper T2 og T4, er av identiske resultater. Så de ærlig forskjellige gruppene er grupper T1 og T2 eller T3 og T4, siden forskjellen i gjennomsnittsverdiene overstiger HSM -verdien til Tukey -testen.

Det konkluderes med at de beste behandlingene, når det gjelder å maksimere resultatet er T1 eller T3, som er likegyldige fra det statistiske synspunktet. For å velge mellom T1 og T3, bør andre faktorer utenfor analysen som presenteres her søkes. For eksempel pris, tilgjengelighet osv.

Referanser

1. Cochran William og Cox Gertrude. 1974. Eksperimentelle design. Trillas. Mexico. Tredje gjentrykk. 661p.
2. Snedecor, g.W. Og Cochran, w.G. 1980. Statistiske metoder. Syvende utg. Iowa, Iowa State University Press. 507p.
3. Stål, r.G.D. Og Torrie, J.H. 1980. Prinsipper og prosedyrer for statistikk: En biometrisk tilnærming (2. utg.). McGraw-Hill, New York. 629p.
4. Tukey, J. W. 1949. Individuell sammenligningsmidler i variansanalysen. Biometrics, 5: 99-114.
5. Wikipedia. Tukey's test. Hentet fra: i.Wikipedia.com