Posisjonstiltak, sentral tendens og spredning

De Målinger av sentral, spredning og posisjons tendens, Dette er verdier som brukes til å tolke et sett med statistiske data på riktig måte. Disse kan arbeides direkte, som hentes fra den statistiske studien, eller de kan organiseres i grupper med like frekvens, noe som letter analysen.

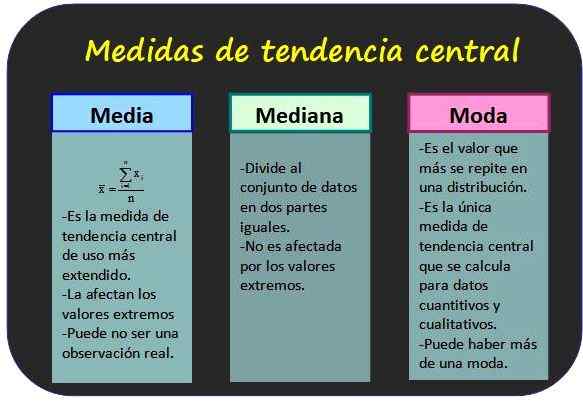
De tre mest kjente sentrale trendtiltakene og noen av dens egenskaper. Kilde: f. Zapata.

Målinger av sentral tendens

De tillater å vite om hvilke verdier de statistiske dataene er gruppert sammen.

Aritmetisk gjennomsnitt

Det er også kjent som gjennomsnittet av verdiene til en variabel og oppnås ved å legge til alle verdiene og dele resultatet med det totale antallet data.

• Aritmetisk gjennomsnitt for data uten gruppering

Være en x -variabel som det ikke er data uten å organisere eller gruppere, det aritmetiske gjennomsnittet beregnes som følger:

Og i sammendraget notasjon:

Eksempel

Eierne av et vandrerhjem med fjellturist har til hensikt å vite hvor mange dager i gjennomsnitt besøkende som gjenstår i fasilitetene. For å gjøre dette ble det utført en registrering av dagene med varighet av 20 grupper av turister, og innhentet følgende data:

1; 1; 2; 2; 1; 4; 5; 1; 3; 4; 5; 4; 3; 1; 1; 2; 2; 3; 4; 1

De gjennomsnittlige dagene turister blir værende er:

= 2.5 dager

• Aritmetisk gjennomsnitt for grupperte data

Hvis de variable dataene er organisert i en absolutt frekvenstabell F_Yo Og klassesentre er x₁, x₂,..., x_n, Gjennomsnittet beregnes av:

I summeringen av sommeren:

Median

Medianen til en gruppe N -verdier av variabel x er den sentrale verdien av gruppen, forutsatt at verdiene i økende grad blir bestilt. På denne måten er halvparten av alle verdiene lavere enn mote, og den andre halvparten er større.

• Medium av ikke -grupperte data

Følgende tilfeller kan presenteres:

-Nummer n verdier av variabel x  merkelig: Medianen er verdien som er bare midt i verdikruppen:

-Nummer n verdier av variabel x par: I dette tilfellet beregnes medianen som gjennomsnittet av de to sentrale verdiene i datagruppen:

Eksempel

For å finne medianen av turisthosteldataene blir de først bestilt fra minst til største:

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5

Det kan tjene deg: Hva er den relative frekvensen og hvordan den beregnes?

Datatummeret er til og med, derfor er det to sentrale data: x₁₀ og x_elleve Og ettersom begge er verdt 2, er gjennomsnittet også.

Median = 2

• Medium av grupperte data

Følgende formel brukes:

Symbolene i formelen betyr:

-C: Intervallbredde som inneholder median

-B_M: Nedre kant av det samme intervallet

-F_m: Antall observasjoner som inneholder intervallet som medianen tilhører.

-N: Total data.

-F_BM: Antall observasjoner før intervallet som inneholder medianen.

Mote

Mote for ikke -grupperte data er den mest frekvensverdien, mens det for grupperte data er den mest frekvensklassen. Det regnes som mote som de mest representative data eller distribusjonsklasse.

To viktige egenskaper ved dette tiltaket er at et datasett kan ha mer enn en mote, og mote kan bestemmes for både kvantitative data og kvalitative data.

Eksempel

Fortsetter med dataene fra turisthjemmet, den som gjentas mest er 1, derfor er det vanligste at turister forblir 1 dag på vandrerhjemmet.

Målinger av spredning

Spredningstiltak beskriver hvor gruppert dataene rundt de sentrale tiltakene er.

Område

Det beregnes ved å trekke fra hoveddataene og mindre data. Hvis denne forskjellen er stor, er det et tegn på at dataene er spredt, mens de små verdiene indikerer at dataene er nær gjennomsnittet.

Eksempel

Utvalget for turisthosteldataene er:

Rekkevidde = 5-1 = 4

Forskjell

• Varians for ikke -grupperte data

For å finne variansen s² Det er nødvendig å først kjenne til det aritmetiske gjennomsnittet, deretter beregnes forskjellen til torget mellom hver data og gjennomsnittet, alle blir lagt til og delt på de totale observasjonene. Disse forskjellene er kjent som avvik.

Variansen, som alltid er positiv (eller null), indikerer hvor langt er observasjonene av gjennomsnittet: Hvis variansen er høy, er verdiene mer spredt enn når variansen er liten.

Eksempel

Variansen for dataene fra turisthjemmet er:

1; 1; 2; 2; 1; 4; 5; 1; 3; 4; 5; 4; 3; 1; 1; 2; 2; 3; 4; 1

= 1.95

• Varians for grupperte data

For å finne variansen til en gruppe grupperte data, er de påkrevd: i) gjennomsnittet, ii) frekvensen f_Yo  som er de totale dataene i hver klasse og iii) x_Yo  eller klasseverdi:

Det kan tjene deg: Typer trekanter

Standardavvik

Standardavviket er den positive kvadratroten til variansen, så den har en fordel i forhold til variansen: den kommer i de samme enhetene som variabelen som er undersøkt og har dermed en mer direkte idé enn det nære eller langt som er variabelen av gjennomsnittet.

• Standardavvik for ikke -grupperte data

Det bestemmes ganske enkelt ved å finne kvadratroten av variansen for ikke -ristede data:

 Eksempel

Standardavviket for turisthosteldata er:

S = √ (s²) = √1.95 = 1.40

• Standardavvik for grupperte data

Det beregnes ved å finne kvadratroten til variansen for grupperte data:

Posisjonstiltak

Posisjonstiltak deler et ordnet sett med data i like deler. Medianen, i tillegg til å være et sentralt tendensmål er også et mål på posisjon, siden det deler helheten i to like store deler. Men du kan skaffe mindre deler med kvartiler, desiler og persentiler.

Kvartiler

Kvartiler deler settet i fire like deler, hver med 25 % av dataene. De er betegnet som q₁, Q₂ og q₃ Og medianen er kvartilen q₂. På denne måten er 25% av dataene under kvartilen q₁, 50% under kvartilen q₂ eller median og 75% under kvartilen q₃.

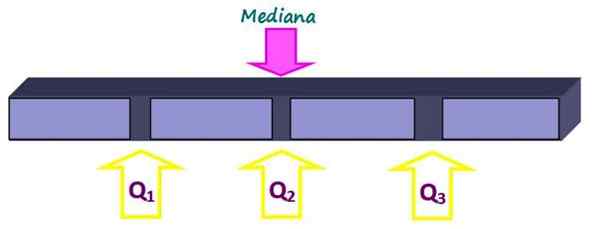Figur 2. Kvartiler deler datasettet i fire like deler. Kilde: f. Zapata.

• Kvartiler for ikke -grupperte data

Dataene bestilles og totalen er delt inn i 4 grupper med samme antall data hver. Posisjonen til den første kvartilen finnes av:

Q₁ = (n+1)/4

Å være de totale dataene. Hvis resultatet er hele dataene som tilsvarer den posisjonen, men hvis det er desimal, er dataene som tilsvarer hele delen med følgende gjennomsnitt, eller for større presisjon er det lineært interpolert mellom nevnte data.

Eksempel

Posisjonen til den første kvartilen q₁ For dataene fra turisthjemmet er:

Q₁ = (n+1) / 4 = (20+1) / 4 = 5.25

Dette er plasseringen av kvartil 1, og ettersom resultatet er desimal, søkes data x data₅ og x_6, som er henholdsvis x₅ = 1 og x₆ = 1 og de er gjennomsnittlig, noe som resulterer:

Første kvartil = 1

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5.

Posisjonen til den andre kvartilen q₂ er:

Kan tjene deg: Teleskopisk sum: Hvordan det løses og løses øvelser

Q₂ = 2 (n+1)/4 = 10.5

Som er gjennomsnittet mellom x₁₀ og x_elleve og sammenfaller med medianen:

Andre kvartil = median = 2

Den tredje kvartilposisjonen beregnes av:

Q₃ = 3 (n+1) / 4 = 3 (20+1) / 4 = 15.75

Det er også desimal, derfor er x gjennomsnittet_femten og x₁₆:

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5.

Men ettersom begge er verdt 4:

Tredje kvartil = 4

Den generelle formelen for plasseringen av kvartiler i uforsvarlige data er:

Q_k = K (n+1)/4

Med k = 1,2,3.

• Kvartiler for grupperte data

De beregnes lik median:

Forklaringen på symbolene er:

-B_Q: Nedre kant av intervallet som inneholder kvartil

-C: Bredde på det intervallet

-F_q: Antall observasjoner inneholdt kvartilintervallet.

-N: Total data.

-F_BQ: Antall data før intervallet som inneholder kvartil.

Dekiler og persentiler

Deciles og persentiler deler datasettet i henholdsvis 10 like deler og 100 like deler, og beregningen deres utføres analogt med kvartiler for kvartiler.

• Deciles og persentiler for ikke -grupperte data

Formler brukes henholdsvis:

D_k = K (n+1)/10

Med k = 1,2,3… 9.

Desil d₅ Det må være lik medianen.

P_k = K (n+1)/100

Med k = 1,2,3… 99.

Persentilen p_femti Det må være lik medianen.

Eksempel

I eksemplet med turisthjemmet, stillingen til D₃ er:

D₃ = 3 (20+1)/10 = 6.3

Hvordan er et desimaltall i gjennomsnitt x₆ og x_7, begge lik 1:

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5

Betyr at 3 tideler av dataene er under x₇ = 1 og de resterende ovenfor.

• Deciles og persentiler for grupperte data

Formlene er analoge med kvartiler. D brukes til å betegne desilene og P for persentilene, og symbolene tolkes på lignende måte:

Den empiriske regelen

Når dataene distribueres symmetrisk og fordelingen er unimodal, er det en regel kalt  Empirisk styre enten Regel 68 - 95 - 99, som grupperer dem i følgende intervaller:

• 68% av dataene er i intervallet:

• 95% av dataene er i intervallet:

• 99% av dataene er i intervallet:

Eksempel

I hvilket intervall er 95% av turisthosteldataene?

De er i intervallet: [2.5−1.40; 2.5+1.40] = [1.1; 3.9].

Referanser

1. Berenson, m. 1985. Statistikk for administrasjon og økonomi. Inter -American s.TIL.
2. Devore, J. 2012. Sannsynlighet og statistikk for ingeniørfag og vitenskap. 8. Utgave. Cengage.
3. Levin, r. 1988. Statistikk for administratorer. 2. Utgave. Prentice Hall.
4. Spiegel, m. 2009. Statistikk. Schaum -serien. 4 ta. Utgave. McGraw Hill.
5. Walpole, r. 2007. Sannsynlighet og statistikk for ingeniørfag og vitenskap. Pearson.