Poisson -koeffisientkoeffisient, formler, verdier, eksempler

Han Poisson -koeffisient Det er en dimensjonsløs mengde, karakteristisk for hvert materiale. Det er en indikasjon på deformasjonen av et stykke materiale før anvendelsen av visse innsats.

Når et materielt stykke som gjennomgår spenning, eller komprimering, lider av en deformasjon, er kvotienten mellom tverrgående deformasjon og langsgående deformasjon nettopp Poisson -koeffisienten.

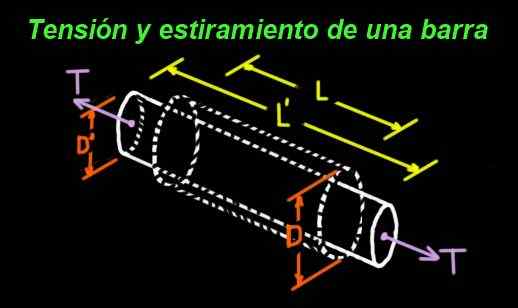
Figur 1. Poissons koeffisient måler forholdet mellom langsgående strekk og tverrgående innsnevring. (Utarbeidet av Ricardo Pérez)

For eksempel strekkes en gummisylinder som gjennomgår spenning i endene i lengderetningen, men den er tverrgående smal. Figur 1 viser en stolpe hvis opprinnelige dimensjoner er: lang l og diameter d.

Stangen blir utsatt for en T -spenning med endene, og som en konsekvens av denne spenningen lider en strekning, slik at den nye lengden er l '> l. Men når man strekker seg, oppstår en innsnevring av diameteren også den nye verdien: D ' < D.

Kvotienten mellom strekk (positiv) og innsnevring (negativ) multiplisert med (-1), er et positivt tall mellom 0 og 0,5. Dette tallet er den så -kalt Poisson v -koeffisienten (gresk brev).

[TOC]

Poisson -koeffisientformel

For å beregne Poisson -koeffisienten er det nødvendig å bestemme den langsgående og tverrgående enhetsdeformasjonen.

Longitudinal enhetsdeformasjon ε_L Det er strekningen delt mellom den opprinnelige lengden:

ε_L = (L ' - l) / l

Tilsvarende tverrgående enhetsdeformasjon ε_T Det er den radiale innsnevringen delt mellom den opprinnelige diameteren:

ε_T = (D ' - d) / d

Derfor beregnes Poisson -koeffisienten med følgende formel:

ν = - ε_T / ε_L 

Forhold til elastisitetsmodulen og stivhetsmodulen

Poisson v koeffisient er relatert til modulen OG av elastisitet (eller ung modul) og med stivhetsmodulen G, etter følgende formel:

Kan tjene deg: Geometrisk optikk: Hvilke studier, lover, applikasjoner, øvelser

ν = e /(2g) - 1

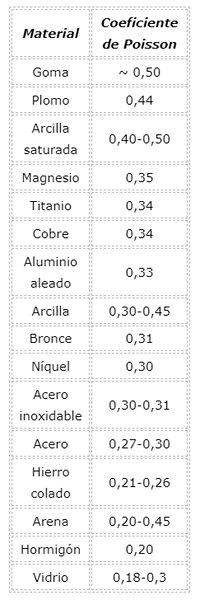
Poisson koeffisientverdi for materialer

Figur 2. Rustfritt stål har Poisson -koeffisient mellom 0,30 og 0,31. Kilde: Pixabay.

Eksempler på beregning

Eksempel 1

En stang med en viss plastmateriale har en lengde på 150 mm og sirkulær seksjon på 20 mm i diameter. Når en kompresjonskraft på 612,25 kg-f blir utsatt for en kompresjonskraft, observeres en forkortelse på 14 mm og samtidig en økning på 0,85 mm i diameteren på stangen.

Regne ut:

a) Longitudinal enhetlig deformasjon.

b) Tverrgående enhetlig deformasjon.

c) Poissons koeffisient for det materialet.

d) Youngs elastisitetsmodul som tilsvarer materialet.

e) Stivhetsmodulen for den plasten.

Løsning på

Husk at deformasjon av langsgående enhet εl er strekningen delt på den opprinnelige lengden:

εl = (l ' - l) / l

εl = (-14 mm) / 150 mm = -0.0933

Merk at den langsgående enhetsdeformasjonen er dimensjonsløs, og i dette tilfellet har den gitt negativt fordi det var en reduksjon i dens langsgående dimensjon.

Løsning b

Tilsvarende er enhetlig tverrgående deformasjon εt radiell innsnevring, delt på den opprinnelige diameteren:

εt = (d ' - d) / d

εt = (+0,85 mm) / 20 mm = 0,0425

Tverrgående enhetlig deformasjon har vært positiv fordi det har vært en økning i stangens diameter.

Løsning c

For beregningen av Poisson -koeffisient må vi huske at den er definert som det negative av kvotienten mellom tverrgående deformasjon og langsgående deformasjon:

ν = - εt / εl 

v = - 0,0425 / (-0,0933) = 0,4554

Det må huskes at Poissons koeffisient er et positivt dimensjonsløst tall, og for de fleste materialer er det mellom 0 og 0,5.

Kan tjene deg: darcy lov

Løsning d

Youngs elastisitetsmodul, betegnet med bokstav E, er proporsjonalitetskonstanten i Hooke's Law. Gjennom E er den normale innsatsen σl relatert til enhetsdeformasjonen εl, som følger:

σl = e εl 

Normal innsats er definert som kvotienten mellom normalkraften (i dette tilfellet parallelt med linjens akse) og tverrsnittet:

σl = f / a = f / (π / 4 * d^2)

I denne øvelsen er Force F 612,25 kg-f, som vil bli gjort til Newtons som er styrkenheten:

F = 612,25 kg-f = 612,25 * 9,8 n = 6000 n = 6 kN

For sin del er tverrsnitt A:

A = (π/4 * d^2) = (3,1416/4) * (20 * 10^-3 m)^2 = 3,1416 * 10^-4 m^2

Endelig er den normale innsatsen som brukes på linjen:

σl = f / a = 6000 n / 3,1416 * 10^-4 m^2 = 19.098.593 PA = 19.098 MPA

For å beregne Youngs elastisitetsmodul klarer vi og av Hooke's Law σl = E εl:

E = σl / εl = 19.098.593 PA / 0,0933 = 204,7 MPa

Løsning e

R -stivhetsmodulen er relatert til Youngs EG -modul og Poisson v -koeffisienten med denne formelen:

E / (2 g) = 1 + v 

Derfra kan du fjerne G:

G = e / (2 (1 + v)) = 204,7 MPa / (2 (1 + 0.4554)) = 70.33 MPa

Eksempel 2

Du har en kabel på 4 mm og 1 m lang diameter. Når vi vet at den kobber unge modulen er 110000 MPa og at Poisson-koeffisienten er 0,34, estimerer den at strekking og innsnevring i diameter som ledningen lider når en vekt på 100 kg-f.

Løsning

For det første er det nødvendig å beregne den normale trekkarbeidet som vekten utøver på ledningen, etter denne formelen:

Kan tjene deg: Vektorer i rommet: Hvordan graf, applikasjoner, øvelser

σl = f / a = f / (π / 4 * d^2)

Kraften F er 980 N og tverrsnittet er:

A = (π/4 * d^2) = (3,1416/4) * (4 * 10^-3 m)^2 = 1.2566 * 10^-5 m^2

Da er trekkinnsatsen:

σl = 980 N / 1,2566 * 10^-5 m^2 = 77.986.000 pa

Beregning av deformasjon av enhetlig tråd

Youngs elastisitetsmodul, betegnet ved bokstav E, er proporsjonalitetskonstanten i Hooke's lov som relaterer den normale innsatsen σl til den enhetlige deformasjonen εl:

σl = e εl 

Derfra kan den langsgående enhetsdeformasjonen av kobbertråden tømmes:

εl = σl / e = 77,986 MPa / 110000 MPa = 7,09 * 10^-4

Beregning av tverrgående enhetlig deformasjon

På den annen side, for å kjenne den tverrgående enhetsdeformasjonen, brukes Poisson -koeffisienten:

ν = - εt / εl 

Endelig må du krysse enhetlig deformasjon er: 

εt = -ν εl = -0,34 * 7.09 * 10 ^-4 = -2,41 * 10 ^-4

Kabel absolutt strekkberegning

Til slutt, for å kjenne den absolutte tøyningen av kabelen, må følgende forhold brukes:

ΔL = εl * l = 7.09 * 10^-4 * 1 m = 7.09 * 10^-4 m = 0.709 mm

Det vil si med den vekten kabelen strakte knapt 0,709 millimeter.

Beregning av reduksjonen i diameter

For å oppnå absolutt krymping i diameter bruker vi følgende formel:

ΔD = εt * d = -2,41 * 10 ^-4 * 4 mm = -9,64 * 10 ^-4 mm = -0 000964 millimeter.

Denne innsnevring i diameter er så liten at det er vanskelig å sette pris på med det blotte øye, til og med dets måling krever et høyt presisjonsinstrument.

Referanser

1. Øl f ... Materialmekanikk. 5. plass. Utgave. 2010. Mc Graw Hill. 1-130.
2. Hibbeler R. Materialmekanikk. Åttende utgave. Prentice Hall. 2011. 3-60.
3. Gere J. Materialmekanikk. Åttende utgave. Cengage Learning. 4-220.
4. Giancoli, d. 2006. Fysikk: Prinsipper med applikasjoner. 6. utg. Prentice Hall. 238-242.
5. Valera Negrete, J. 2005. Generelle fysikknotater. Unam. 87-98.