Rektangulære komponenter i en vektor (med øvelser)

De Rektangulære komponenter i en vektor er dataene som utgjør denne vektoren. For å bestemme dem er det nødvendig å ha et koordinatsystem, som vanligvis er det kartesiske planet.

Når du har en vektor i et koordinatsystem, kan komponentene beregnes. Disse er 2, en horisontal komponent (parallell med x -aksen), kalt “komponent i x -aksen”, og en vertikal komponent (parallelt med y -aksen), kalt “komponent i y -aksen” ”.

Grafisk representasjon av de rektangulære komponentene i en vektor

For å bestemme komponentene er det nødvendig.

[TOC]

Hvordan bestemme de rektangulære komponentene i en vektor?

For å bestemme disse komponentene, må visse forhold mellom rektangler og trigonometriske funksjoner være kjent.

I følgende bilde kan du se dette forholdet.

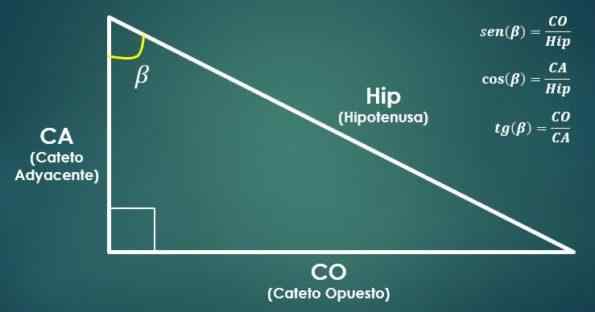Forhold mellom rektangler og trigonometriske funksjoner

Bosomen i en vinkel er lik kvotienten mellom målet på katetoet i motsetning til vinkelen og målet på hypotenusen.

På den annen side er kosinus i en vinkel lik kvotienten mellom målet på kateto ved siden av vinkelen og målet på hypotenusen.

Tangenten i en vinkel er lik kvotienten mellom målet på det motsatte benet og målet på den tilstøtende kateto.

I alle disse forholdene er det nødvendig å etablere den tilsvarende rektangeletrekanten.

Er det andre metoder?

Ja. Avhengig av dataene som er gitt, kan måten å beregne de rektangulære komponentene i en vektor variere. Et annet verktøy som brukes mye er Pythagoras teorem.

Kan tjene deg: eksistens og unikhet teorem: demonstrasjon, eksempler og øvelser

Løste øvelser

Følgende øvelser utførte definisjonen av de rektangulære komponentene i en vektor og forholdene beskrevet ovenfor.

Første trening

Det er kjent at en vektor A har størrelse lik 12 og vinkelen som denne formen med x -aksen har et 30 ° mål. Bestem de rektangulære komponentene i nevnte vektor til.

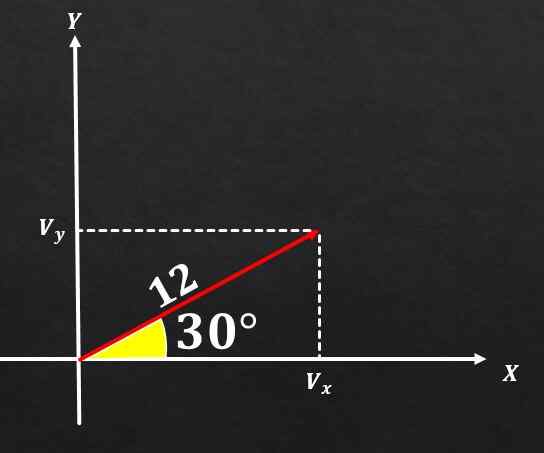
Løsning

Hvis bildet blir verdsatt og formlene beskrevet ovenfor brukes, kan det konkluderes med at komponenten i og vektoren A er lik

sin (30 °) = vy / 12, og derfor vy = 12*(1/2) = 6.

På den annen side er komponenten på x -aksen til vektor a lik

cos (30 °) = vx / 12, og derfor vx = 12*(√3 / 2) = 6√3.

Andre trening

Hvis vektor A har en størrelse lik 5 og komponenten på x -aksen er lik 4, må du bestemme verdien av A -komponenten på Y -aksen.

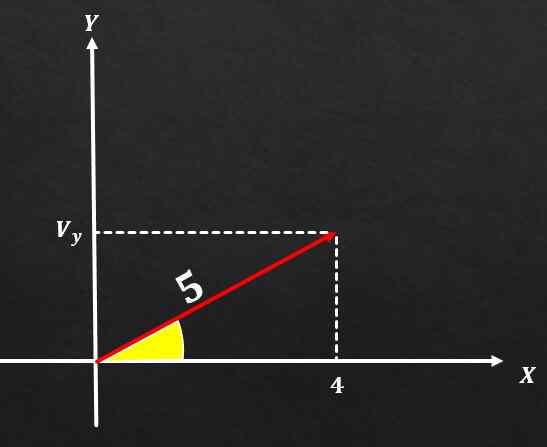
Løsning

Ved å bruke Pythagoras -teoremet, må størrelsen på vektoren en høy kvadrat være lik summen av rutene til de to rektangulære komponentene. Det vil si m² = (vx) ² + (vy) ².

Erstatte verdiene som er gitt, må du

5² = (4) ² + (VY) ², 25 = 16 + (VY) ².

Dette innebærer at (VY) ² = 9 og følgelig VY = 3.

Tredje øvelse

Hvis vektor A har en størrelse lik 4 og denne danner en vinkel på 45 ° med x -aksen, må du bestemme de rektangulære komponentene til nevnte vektor.

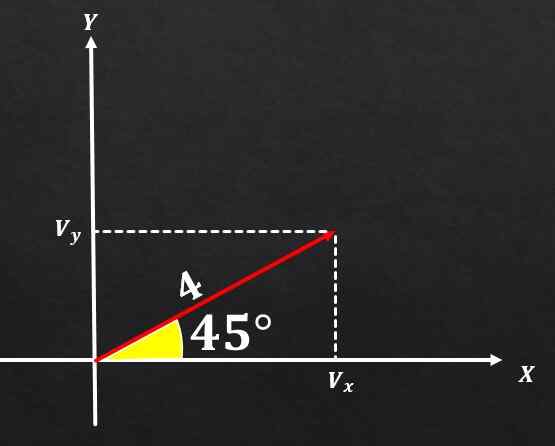
Løsning

Ved å bruke sammenhengene mellom en rektangel -trekant og trigonometriske funksjoner, kan det konkluderes med at komponenten på og vektoren A er lik

sin (45 °) = VY / 4, og derfor VY = 4*(√2 / 2) = 2√2.

På den annen side er komponenten på x -aksen til vektor a lik

Kan tjene deg: sammensatt suksess

cos (45 °) = vx / 4, og derfor vx = 4*(√2 / 2) = 2√2.

Referanser

1. Landaverde, f. D. (1997). Geometri (Reprint Ed.). Framgang.
2. Leake, d. (2006). Trekanter (Illustrert red.). Heinemann-Raintree.
3. Pérez, ca. D. (2006). Forkalkning. Pearson Education.
4. Ruiz, Á., & Barrantes, h. (2006). Geometrier. Cr teknologisk.
5. Sullivan, m. (1997). Forkalkning. Pearson Education.
6. Sullivan, m. (1997). Trigonometri og analytisk geometri. Pearson Education.