Bevaring av det lineære momentia -prinsippet, eksempler, øvelser.

De bevaring av lineær momentum av et legeme fastslår at produktet av massen med hastighetsvektoren er en konstant mengde, når kroppen er fri for interaksjon med andre kropper og med hastigheten målt med hensyn til et fast eller ikke-akutt referansesystem.

Når det bare er flere kropper som samhandler mellom dem, men ikke med det ytre miljøet, så lineær momentum av settet forblir også konstant over tid.

En astronaut i verdensrommet er fri for all samhandling, derfor den lineære øyeblikket

Det lineære øyeblikket, mengden lineær bevegelse eller bare Momentum, Det er betegnet med brevet p Og det er en vektormengde:

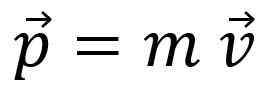
Det lineære øyeblikket er ikke det samme som hastigheten, selv om forholdet er tydelig: for eksempel har en lastebil som går til 20 km/t mer lineær tid enn en sykkel som beveger seg i samme hastighet.

For at det lineære øyeblikket av et legeme skal endres, er det nødvendig at en netto ytre kraft virker på det, ellers forblir den konstant. I tillegg er det lineære øyeblikket P av et system dannet av N-body Det er vektorsummen av individuelle øyeblikk:

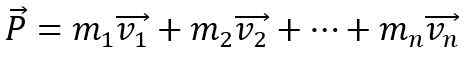
[TOC]

Prinsipp for bevaring av mengden lineær bevegelse

I et organ fritt for krefter (eller en der alle krefter på det blir avlyst) hender det at det lineære øyeblikket.

På samme måte passerer det i et system dannet av flere organer som bare samhandler med hverandre, men ikke med det ytre miljøet: det totale lineære øyeblikket av systemet forblir fast under utviklingen av settet med settet.

Dette bevaringsprinsippet er oppgitt slik:

Det totale lineære øyeblikket av et sett med N-Body som bare samhandler med hverandre, men ikke med det ytre miljøet, er en ufravikelig mengde i tid.

Og matematisk uttrykkes det som følger:

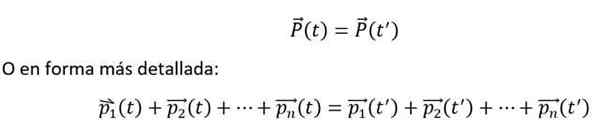
Den tidligere likheten er oppfylt, hvis og bare hvis n-Kropper samhandler med hverandre, men ikke med det ytre miljøet. I tillegg bør individuelle øyeblikk alltid måles med hensyn til et treghetsreferansesystem.

Eksempler

Eksempel 1

To astronauter i verdensrommet er hentet fra hendene og forblir i en fast stilling med hensyn til skipet. Men de presser hverandre, de begynner å skille seg i motsatte retninger, når de blir sett fra skipet.

Det kan tjene deg: Teori om Big Bang: Kjennetegn, stadier, bevis, problemer

I dette tilfellet, ettersom samspillet mellom astronauter bare er blant dem gjennom kontaktkraften i hendene, det totale lineære øyeblikket. Det vil si total lineær tid 0.

Imidlertid endret det lineære øyeblikket av hver astronaut. Opprinnelig hadde hver et lineært øyeblikk 0 med hensyn til skipet, men etter å ha dyttet den ene kommer ut i den ene retningen og den andre i motsatt retning, med ikke-null lineære øyeblikk med lik størrelsesorden og motsatte adresser.

Når de enkelte øyeblikkene blir tilsatt vektor, oppnås den opprinnelige totale lineære momentumet som et resultat, som er ugyldig.

På den annen side bevaring av beløpet lineært øyeblikk. Men resultatet av å multiplisere massen med hastigheten er lik produktet oppnådd ved å multiplisere massen til det andre med hastigheten til den andre.

Eksempel 2

En valp er på en flytende plattform i en innsjø med rolig vann, og eieren ser den fra en dock. I begynnelsen er både plattformen og valpen i ro, men når valpen vil henvende seg til eieren, beveger plattformen seg bort fra kaien.

Forklaringen på denne observasjonen er nettopp i prinsippet om bevaring av det lineære momentumsmengden. Systemet består av valpen og plattformen.

Valpen kan gå på plattformen takket være friksjonskraften mellom bena og overflaten, i dette tilfellet er friksjonskraften en intern kraft av samhandling mellom den og plattformen.

Settet er et isolert system, og plattformen kan bevege seg horisontalt på sjøen, fri for all bevegelsesmotstand. På den annen side, i vertikal retning, er alle kreftene balanse og kompensert, og settet har ingen bevegelse i den retningen.

Derfor blir alle hypotesene i denne situasjonen oppfylt slik at prinsippet om bevaring av det lineære momentumet blir brukt.

Eksempel 3

En Eskimo blir fanget i midten av en is, isen er så glatt at uansett hvor mye prøvd, glir Eskimo og forblir alltid på samme sted.

Den eneste mulige måten Eskimo forlater innsjøen, er at den ligger i retningen i motsetning til et tungt objekt som bærer i ryggsekken (forutsatt en).

Kan tjene deg: Geometrisk optikk: Hvilke studier, lover, applikasjoner, øvelser

applikasjoner

Skip i verdensrommet

Bevaring av det lineære øyeblikket. I dette tilfellet oppnås impulsen til skipet ved utvisning av gasser i høy hastighet, slik at raketten kan bevege seg i motsatt retning som de ble utvist.

Hvis skipet opprinnelig er i ro, oppstår når drivstoffet blir brent og utvist, oppstår kraften mot selve skipet. Det er en intern kraft mellom gasser og skipet. Det er ingen ytre krefter og bruker derfor bevaring av det lineære øyeblikket.

Ettersom det lineære øyeblikket av gasser er det samme og i strid med skipets, klarer det å forlate hvile, og ved å fortsette å utvise gasser øker bevegelsesmengden og derfor hastigheten.

Dagliglivet

En annen sak for bevaring av det lineære øyeblikket.

Det kan hevdes at i dette tilfellet ikke prinsippet gjelder, fordi det er en ytre kraft: motstanden som treet tilbyr til nelliket.

På kontakttidspunktet er imidlertid styrken som hammeren skriver ut til neglen en intern kraft (mellom systemet som er neglen og hammeren) mye større enn motstanden som treverket motsetter seg, og derfor er sistnevnte ubetydelig ubetydelig.

Hele den lineære øyeblikket av hammeren, som er ganske stort på grunn av sin store masse og hastighet, overføres til spikeren like etter kollisjonen. Merk at hele øyeblikket overføres, men ikke all den kinetiske energien til hammeren, siden en del av den blir omgjort til termisk energi til neglen og hammeren, som øker temperaturen etter påvirkningen.

Øvelser

Oppgave 1

Andrew og Berenice astronauter er ute av romstasjonen hentet fra begge hender og i ro med hensyn til stasjonen. De kjører skyver hendene mot de av den andre, og de blir løslatt. Hvis Andrew, 70 kg masse, beveger seg på 1 m/s med hensyn til stasjonen, hva er Berenices hastighet med 49 kg masse?

Løsning

I dette tilfellet blir hypotesen om bevaring av det lineære momentumet tydelig anvendt, siden det ikke er noen ytre krefter i ytre rom. Styrken som hendene skyver begge astronautene er en intern kraft.

Det kan tjene deg: bølgediffraksjon: konsept og eksempler

Anta at Andrews masse er m_til og den fra Berenice m_b. Tilsvarende er hastighetene til begge etter impulsen V_til For Andrew og V_b For Berenice. Deretter brukes bevaring av det lineære momentumet som følger:

M_til∙0 + M_b∙0 = M_til∙V_til+ M_b∙V_b

Rydde Berenices hastighet du har:

V_b = - (m_til / M_b) ∙ V_til

Plassering av numeriske verdier:

V_b = - (70/49) ∙ (1m / s) eller = -1,43 m/s eller

Det vil si at Berenice beveger seg raskt 1,43 m/s i motsatt retning av Andrew.

Oppgave 2

En valp går mot eieren på toppen av en semi-sftet plattform. Kilde: f. Zapata.

En 5 kg deig er i ro på en 15 kg plattform som flyter, også i ro. Hvis valpen begynner å gå på plattformen med en hastighet på 0,5 m/s med hensyn til dette. Hvor raskt vil valpen og plattformen angående en fast observatør til bakken?

Løsning

Det vil bli tatt som et treghetsreferansesystem til kaien der valpeieren er. Opprinnelig er både valpen og den flytende plattformen i ro med hensyn til kaien.

Når valpen bestemmer seg for å gå mot eieren raskt V ' Når det gjelder plattformen, beveger plattformen seg bort fra våren med hastighet +V. Hastigheten til valpen med hensyn til kaien oppnås med vektorsummen av hastigheten med hensyn til plattformen pluss hastigheten på plattformen og betegner den med:

v = -v' + V

Ettersom vannmotstanden mot bevegelsen av plattformen praktisk talt er null på grunn av den lave hastigheten, kan det bekreftes at systemet som består av Valpen + plattformen Det er et isolert system og prinsippet om bevaring av det lineære momentumet brukes:

0 = m ∙ V + M ∙ V

Husker at V = V ' + V du har:

0 = -M ∙ V ' + M ∙ V + M ∙ V

Det vil si: m ∙ v '= (m+m) ∙ V

Derfor v = [m/(m + m)] v 'y v = - (m/m) v = - [m/(m + m)] v'

Erstatte numeriske verdier er:

V = [5/(5 +15)] ∙ 0,5 m/s = 0,125 m/s

Dette er hastigheten som vårplattformen beveger seg bort.

V = -(15/20) ∙ 0,5 m/s = -0,375 m/s

Og dette er hastigheten som valpen nærmer seg kaien.

Referanser

1. Duke University. Systemer for partikler. Gjenopprettet fra: Webhome.Phy.hertug.Edu.
2. Rex, a. 2011. Fundamentals of Physics. Pearson.
3. Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Ed. Volum 1. Pearson.
4. Serway, r., Jewett, J. (2008). Fysikk for vitenskap og ingeniørfag. Volum 1. 7. Ed. Cengage Learning.
5. Tipler, s. (2006). Fysikk for vitenskap og teknologi. 5. utg. Volum 1. Redaksjon tilbake.