Rektangulære koordinater eksempler og øvelser løst

De Rektangulære koordinater o Kartesiske er de som er oppnådd når de er projisert ortogonalt på de tre kartesiske aksene X, Y, Z, et punkt som ligger i det tre -dimensjonale rommet.

Kartesiske akser er gjensidig vinkelrett orientert rett. I det kartesiske koordinatsystemet blir tre reelle tall som er dets rektangulære koordinater tilordnet hvert punkt i rommet.

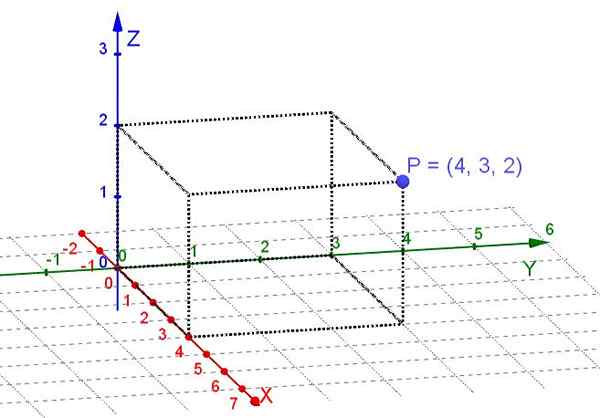
Figur 1. Rektangulære koordinater av punkt P (egen utdyping)

Et fly er et underområde med tre -dimensjonalt rom. I tilfelle å vurdere punkter på et fly, er det nok å velge et par vinkelrett akser x, og som et kartesisk system. Da på hvert punkt på flyet blir to reelle tall tildelt ham at hans rektangulære koordinater er.

[TOC]

Opprinnelse til rektangulære koordinater

De rektangulære koordinatene ble opprinnelig foreslått av den franske matematikeren René Descartes (1596 og 1650), og det er grunnen til at de mottar kirkesamfunn av kartesere.

Med denne ideen om Descartes er punktene i flyet og rommet tildelt tall, slik at de geometriske figurene har assosiert en algebraisk ligning og de klassiske geometriske teoriene kan demonstreres algebraisk. Med kartesiske koordinater ble analytisk geometri født.

Det kartesiske flyet

Hvis det er valgt på et plan to vinkelrett linjer som krysser hverandre på et tidspunkt eller; og hvis også hver linje tildeles en retning og en numerisk skala mellom påfølgende like store punkter, er det da et kartesisk system eller plan der hvert punkt i flyet er assosiert med et ordnet par to reelle tall som er dets anslag på henholdsvis på x og y akser.

Poeng A = (3, 2); B = (-2, 3); C = (-2, -3) og d = (3, -3) er representert i det kartesiske planet som vist nedenfor:

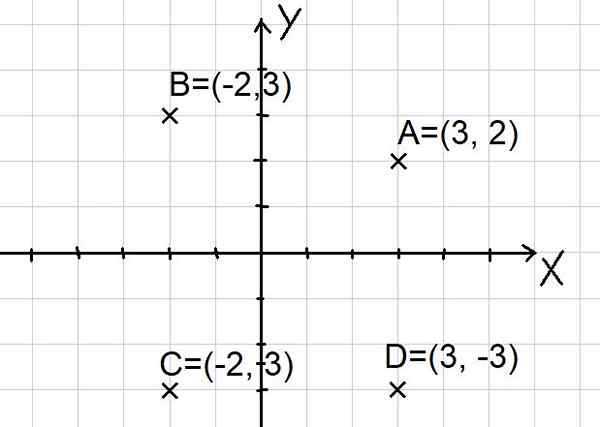Figur 2. Peker på det kartesiske flyet. (Egen utdyping)

Merk at de to x- og y -aksene deler flyet i fire sektorer som kalles kvadranter. Punkt A er i den første kvadranten, B i den andre kvadranten, C i den tredje kvadranten og punkt D i den fjerde kvadranten.

Kan tjene deg: befolkning og prøve

Avstand mellom to punkter

Avstanden mellom to punkter A og B i det kartesiske planet er lengden på segmentet som forener dem. Denne avstanden kan beregnes analytisk som følger:

D (a, b) = √ (bx - øks)^2 + (av - ay)^2)

Den fremre formelen oppnås ved å bruke Pythagoras -teoremet.

Bruk av nevnte formel på punktene A, B i figur 2 er:

D (a, b) = √ (-2 - 3)^2 + (3 - 2)^2) = √ (-5)^2 + 1^2) = √ (26)

Det vil si at d (a, b) = 5,10 enheter. Merk at avstanden ble oppnådd uten behov for å måle med en regel, er en fullstendig algebraisk prosedyre blitt fulgt.

Analytisk uttrykk for en linje

Rektangulære koordinater tillater analytisk representasjon av grunnleggende geometriske objekter som punktet og linjen. To punkter A og B definerer en enkelt linje. Linjens helning er definert som kvotienten mellom forskjellen i koordinater og punkt B mindre, delt på forskjellen i x -koordinatene til punkt B mindre A:

Venter = (av - ay)/(BX - AX)

Et hvilket som helst punkt med koordinater (x, y) som tilhører linjen (AB) må ha samme skråning:

Venter = (y - ay)/(x - øks)

Ligningen som oppnås ved likheten i bakkene er den analytiske eller algebraiske representasjonen av linjen som passerer gjennom punktene A og B:

(y - ay)/(x - ax) = (av - ay)/(bx - ax).

Hvis du blir tatt for A og B er de rektangulære koordinatene til figur 2:

(Y - 2)/(x - 3) = (3 - 2)/( - 2 - 3)

(y - 2)/(x - 3) = -⅕

I dette tilfellet er det en linje med en negativ skråning -⅕, som betyr at det ligger på et punkt på linjen og øker X -koordinaten i en enhet, koordinaten og reduseres i 0,2 enheter. 

Kan tjene deg: Toroid eller Toro Dona

Den mest vanlige måten å skrive ligningen på linjen i flyet er med koordinaten og tydelig som en funksjon av variabel x:

y = -(1/5) x + 13/5 

Eksempler

Eksempel 1

Oppnå ved analysemetoder Avstanden mellom punktene C og A, som de rektangulære koordinatene til C = (-2, -3) og de av A = (3.2).

Formelen for den euklidiske avstanden mellom disse to punktene er skrevet slik:

D (a, c) = √ ((cx - ax)^2 + (cy - ay)^2)

Erstatte de tilsvarende rektangulære koordinatene du har:

D (a, c) = √ (-2-3)^2 + (-3-2)^2) = √ (-5)^2 + (-5)^2) = 5√2 = 7.07

Eksempel 2

Få ligningen på linjen som passerer gjennom punkt C av koordinater (-2, -3) og punktet P for koordinat (2, 0).

Først oppnås skråningen på CP -linjen:

Venter = (0 -(-3)) / (2 -( -2)) = ¾ 

Et hvilket som helst punkt q av generiske rektangulære koordinater (x, y) som tilhører CP -linjen, må ha samme skråning:

Venter = (y -(-3)) / (x -( -2)) = (y +3) / (x +2)

Det vil si at ligningen på CP -linjen er:

(Y +3) / (x +2) = ¾

En alternativ måte å skrive ligningen på CP -linjen er å rydde og:

y = ¾ x - 3/2 

Løste øvelser

Oppgave 1

Få de rektangulære koordinatene til skjæringspunktet mellom linjene y = - (1/5) x + 13/5 og linjen y = ¾ x - 3/2.

Løsning: Per definisjon deler skjæringspunktet for de to linjene de samme rektangulære koordinatene. Derfor er koordinater og på skjæringspunktet identisk for begge linjene:

-(1/5) x + 13/5 = ¾ x - 3/2

Hva som fører til følgende uttrykk:

Kan tjene deg: Rektangel trapesoid: egenskaper, forhold og formler, eksempler

(¾ + ⅕) x = 13/5 +3/2

Å løse summen av brøk oppnås:

19/20 x = 41/10

Rydding x:

x = 82/19 = 4.32

For å oppnå verdien og krysset, erstattes x -verdien oppnådd i en av linjene:

y = ¾ 4.32 - 3/2 = 1,74

Dette betyr at de gitte linjene blir oppfanget på punkt I av koordinater I = (4,32; 1,74).

Oppgave 2

Få omkretsligningen som passerer gjennom den rektangulære koordinatpunktet R (3, 4) og som har et senter ved koordinatens opprinnelse.

Løsning: Radio R er avstanden fra punkt R til opprinnelse eller koordinater (0, 0).

d (r, o) = √ ((rx - 0)^2 + (ry - 0)^2) = √ ((3 - 0)^2 + (4 - 0)^2) = √ (3^2 + 4^2) = √ (9 + 16) = √ (25) = 5

Det vil si at det er en Radius 5 Circle 5 sentrert på (0,0).

Et hvilket som helst punkt P (x, y) av omkretsen må ha samme avstand 5 til sentrum (0, 0) for hva som kan skrives:

D (p, o) = √ ((x - 0)^2 + (y - 0)^2) = √ (x^2 + y^2) = 5

Det er å si:

√ (x^2 + y^2) = 5

For å eliminere kvadratroten blir begge likhetsmedlemmer stille igjen:

x^2 + y^2 = 25

Hva er omkretsligningen.

Med dette eksemplet er kraften i det rektangulære koordinatsystemet illustrert, som gjør det mulig å bestemme geometriske objekter, for eksempel omkretsen uten behov for å bruke papir, blyant og kompass. Omkretsen som bare forespurt av algebraiske metoder er bestemt.

Referanser

1. Arfken g og weber h. (2012). Matematiske metoder for fysikere. En omfattende guide. 7. utgave. Akademisk presse. ISBN 978-0-12-384654-9
2. CC -beregning. Rektangulære koordinater løste problemer. Gjenopprettet fra: Beregning.DC
3. Weisstein, Eric w. “Kartesiske koordinater.”Fra Mathworld-A Wolfram Web. Gjenopprettet fra: Mathworld.Wolfram.com
4. Wikipedia. Kartesisk koordinatsystem. Hentet fra: i.Wikipedia.com