Sfæriske koordinater eksempler og øvelser løst

De sfæriske koordinater De er et punktstedssystem i det tre -dimensjonale rommet som består av en radial koordinat og to vinkelkoordinater kalt polar koordinat og azimutal koordinat.

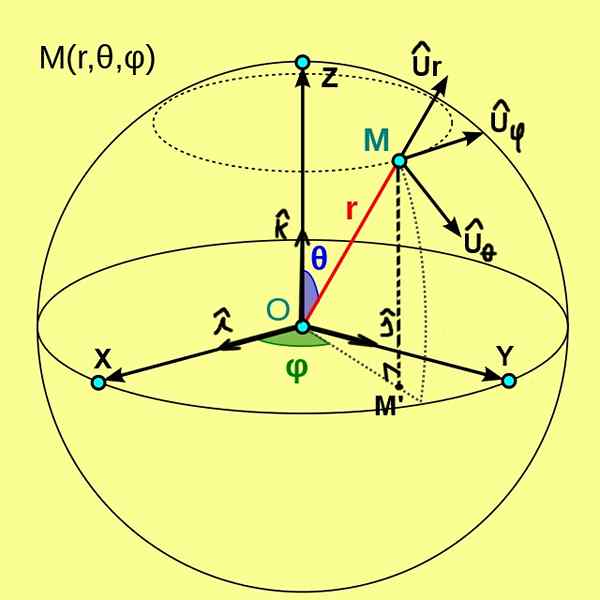
I figur 1, som vi ser nedenfor, vises de sfæriske koordinatene (r, θ, φ) til et punkt m. Disse koordinatene henvises til et ortogonalt system med kartesiske akser x, y, z av opprinnelse eller.

Figur 1. Sfæriske koordinater (r, θ, φ) fra et punkt m. (Wikimedia Commons)

I dette tilfellet er koordinat r av punkt m avstanden fra det punktet til opprinnelsen eller. Den polare koordinaten θ representerer vinkelen mellom den positive semi -aksen Z og vektorradiusen OM. Mens den azimutale koordinaten φ er vinkelen mellom den positive semi -aksen X og vektorradiusen om ', er det m' den ortogonale projeksjonen av M på XY -planet.

Den radiale koordinaten R tar bare positive verdier, men hvis et punkt er plassert ved opprinnelsen, så r = 0. Den polare koordinaten θ tar som en minimumsverdi 0º for punkter som ligger på den positive semistribben. Til slutt tar azimutalkoordinaten φ som en minimumsverdi 0º og maksimalt 360º -nivå.

0 ≤ r < ∞

0 ≤ θ ≤ 180º

0 ≤ φ  < 360º

[TOC]

Endring av koordinater

Deretter vil formlene som tillater de kartesiske koordinatene (x, y, z) til et punkt m, bli gitt, forutsatt at de sfæriske koordinatene til det samme (r, θ, φ) punktet:

x = r sen (θ) cos (φ)

y = r sen (θ) sin (φ) 

z = r cos (θ)

På samme måte er det nyttig å finne forholdene for å bevege seg fra de kartesiske koordinatene (x, y, z) til et punkt gitt til de sfæriske koordinatene til det punktet:

R = √ (x^2 + y^2 + z^2)

θ = Arcan (√ (x^2 + y^2) / z)

Kan tjene deg: diskret tilfeldig variabel

φ = Arctan (y / x)

Vektorbase i sfæriske koordinater

Fra de sfæriske koordinatene er en ortonormal base av basevektorer definert, som er betegnet med Ur, Uθ, Uφ. Figur 1 viser disse tre enhetsvektorene, som har følgende egenskaper:

- Ur Det er enhetsvektoren tangens til den radielle linjen θ = ctt og φ = ctt;

- Uθ Det er enheten tangentvektor til buen φ = ctt og r = ctt;

- Uφ Det er enhetsvektor tangens til bue r = ctt og θ = ctt.

Linje- og volumelementer i sfæriske koordinater

Vektorposisjonen til et punkt i rommet i sfæriske koordinater er skrevet slik:

r = r Ur

Men en uendelig variasjon eller forskyvning av et punkt i det tre -dimensjonale rommet, i disse koordinatene kommer det til uttrykk ved følgende vektorforhold:

dr = dr Ur + r dθ Uθ + r sen (θ) dφ Uφ

Til slutt er en uendelig volum -DV i de sfæriske koordinatene skrevet slik:

dv = r^2 sin (θ) dr dθ dφ

Disse forholdene er veldig nyttige for beregning av linjeintegraler og volum i fysiske situasjoner som har sfærisk symmetri.

Forhold til geografiske koordinater

Geografiske koordinater forstås at de tjener til å lokalisere steder på jordens overflate. Dette systemet bruker koordinatene for breddegrad og lengde for å lokalisere posisjonen på jordens overflate.

I det geografiske koordinatsystemet er det antatt jordoverflaten.

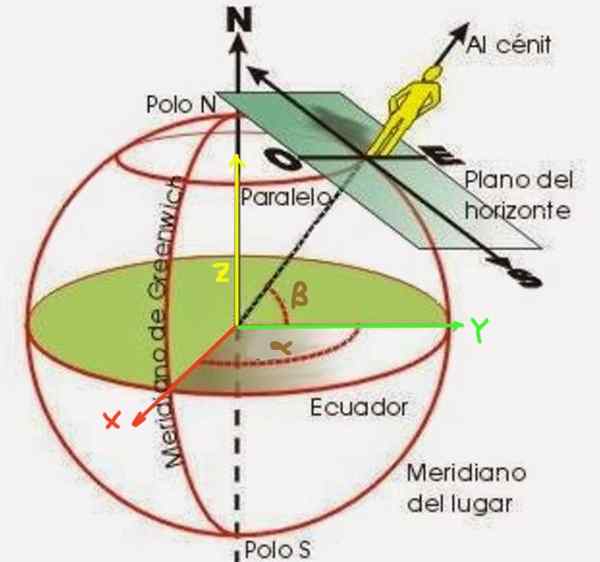Figur 2. Lengde α og β breddegrad av en observatør på jordens overflate.

Β -breddegraden er en vinkel dannet av en radius som starter fra jordens sentrum til det punktet at du vil plassere. Det måles fra ekvatorialplanet, som vist i figur 2. På den annen side er lengden α vinkelen som meridianen til punktet som plasserer form med hensyn til null meridian (kjent som Greenwich Meridian).

Kan tjene deg: relativ verdi

Breddegrad kan være nord eller sørlig breddegrad, avhengig av om stedet som ligger på den nordlige halvkule eller på den sørlige halvkule. Tilsvarende kan lengden være vestover eller dette avhengig av om stedet er vest eller øst for null meridian.

Formler for å endre seg fra geografisk til sfærisk

For å få disse formlene, er det første å etablere et koordinatsystem. XY -planet er valgt sammenfallende med ekvatoriplanet, og er den positive semi -aksen X som går fra jordens sentrum og gjennom null meridian. På sin side, aksen og passerer gjennom 90º og meridian. Jordens overflate har RT -radio.

Med dette koordinatsystemet er geografisk til sfæriske transformasjoner dermed:

αEβN → (RT, θ = 90º-ß, φ = α)

αoβN → (RT, θ = 90º-ß, φ = 360º-a)

αeβ → (RT, θ = 90º+β, φ = α)

αoβs → (RT, θ = 90º+β, φ = 360º-a) 

Eksempler

Eksempel 1

De geografiske koordinatene til Palma de Mallorca (Spania) er:

Østlengde 38.847º og Northern Latitude 39.570º. For å bestemme de sfæriske koordinatene som tilsvarer Palma de Mallorca, brukes den første av formlene i de forrige seksjonsformlene:

38.847ºe39.570ºN → (r = 6371 km, θ = 90º-39.570º, φ = 38.847º)

Da er de sfæriske koordinatene:

Palma de Mallorca: (r = 6371 km, θ = 50,43º, φ = 38,85º)

I forrige respons er r lik jordens gjennomsnittlige radius.

Eksempel 2

Å vite at Falklandsøyene (Falkland) har geografiske koordinater 59ºO 51,75 ºS, bestem de tilsvarende polare koordinatene. Husk at x -aksen går fra midten av jorden til 0º meridian og på ekvatorialplanet; Y -aksen også i ekvatorialplanet og gjennom 90º West Meridian; Endelig Z-aksen på aksen til terrestrisk rotasjon i sør-nord-retning.

Kan tjene deg: Curtosis: Definisjon, typer, formler, hva er det for for eksempel

For å finne de tilsvarende sfæriske koordinatene bruker vi formlene presentert i forrige seksjon:

59ºO 51,75ºS → (r = 6371 km, θ = 90º+51,75º, φ = 360º-59º) det vil si

Malvinas: (r = 6371 km, θ = 141,75º, φ = 301º)

Øvelser

Oppgave 1

Finn de kartesiske koordinatene til Palma de Mallorca i Cartesiano XYZ referansesystem vist i figur 2.

Løsning: Tidligere, i eksempel 1 ble de sfæriske koordinatene oppnådd basert på de geografiske koordinatene til Palma de Mallorca. Slik at formlene presentert ovenfor kan brukes til å flytte fra sfæriske til kartesere:

x = 6371 km sen (50,43 º) cos (38,85º)

Y = 6371 km sen (50,43 º) sen (38,85º) 

Z = 6371 km cos (50,43º)

Å utføre de tilsvarende beregningene er:

Palma de Mallorca: (x = 3825 km, y = 3081 km, z = 4059)

Oppgave 2

Finn de kartesiske koordinatene til Falklandsøyene i Cartesiano XYZ referansesystem vist i figur 2.

Løsning: Tidligere i eksempel 2 ble de sfæriske koordinatene oppnådd basert på de geografiske koordinatene til Falklandsøyene. Slik at formlene presentert ovenfor kan brukes til å flytte fra sfæriske til kartesere:

x = 6371 km Sen (141,75º) cos (301º)

Y = 6371 km Sen (141,75º) Sen (301º) 

Z = 6371 km cos (141,75º)

Utføre de tilsvarende beregningene oppnås:

Falkland Islands: (x = 2031 km, y = -3381 km, z = -5003)

Referanser

1. Arfken g og weber h. (2012). Matematiske metoder for fysikere. En omfattende guide. 7. utgave. Akademisk presse. ISBN 978-0-12-384654-9
2. CC -beregning. Løst sylindriske og sfæriske koordinatproblemer. Gjenopprettet fra: Beregning.DC
3. Astronomy Workshop. Breddegrad og lengdegrad. Hentet fra: Rate.Blogspot.com/
4. Weisstein, Eric w. “Sfæriske koordinater.”Fra Mathworld-A Wolfram Web. Gjenopprettet fra: Mathworld.Wolfram.com
5. Wikipedia. Sfærisk koordinatsystem. Hentet fra: i.Wikipedia.com
6. Wikipedia. Vektorfelt i sylindriske og sfæriske koordinater. Hentet fra: i.Wikipedia.com