Kvadrilaterale elementer, egenskaper, klassifisering, eksempler

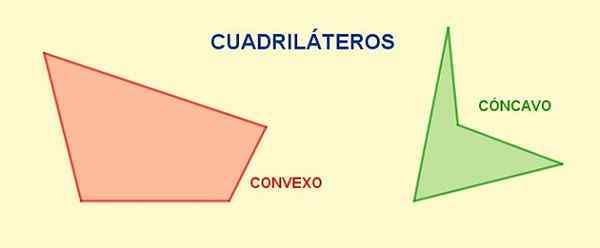
EN kvadrilateral Det er en fire -sidig polygon og fire hjørner. Deres Motsatte sider De er de som ikke har noen vanlige hjørner, mens de er påfølgende sider De som har et felles toppunkt.

I en firkantet er de tilstøtende vinkler De som deler en side, mens Motsatte vinkler De har ingen felles sider. Et annet viktig kjennetegn ved en firkantet er at summen av de fire Interne vinkler Det er dobbelt så stor vinkel, det vil si 360º eller 2π radianer.

Figur 1. Forskjellige firkantede. Kilde: f. Zapata.

Diagonalene De er segmentene som forener et toppunkt med det motsatte og i en gitt ring, fra hvert toppunkt kan du tegne en enkelt diagonal. Det totale antall diagonaler av en firkantet er to.

Kvadrilaterale er figurer kjent for menneskeheten siden eldgamle tider. Arkeologiske poster, så vel som konstruksjonene som overlever i dag, vitner om det.

Også i dag fortsetter kvadrilateralene å ha en viktig tilstedeværelse i hverdagen til alle. Leseren kan finne dette skjemaet på skjermen som teksten leser i dette nøyaktige øyeblikket, i vinduene, dørene, bildelene og utallige steder mer.

[TOC]

Klassifisering av firkantede

I følge parallellismen til de motsatte sidene, er firkantene klassifisert som følger:

1. Trapezoid, Når det ikke er noen parallellisme og den firedoblede er konveks.
2. Trapes, Når det er parallellisme mellom et enkelt par motsatte sider.
3. Parallellogram, Når motsatte sider er parallelle to til to.

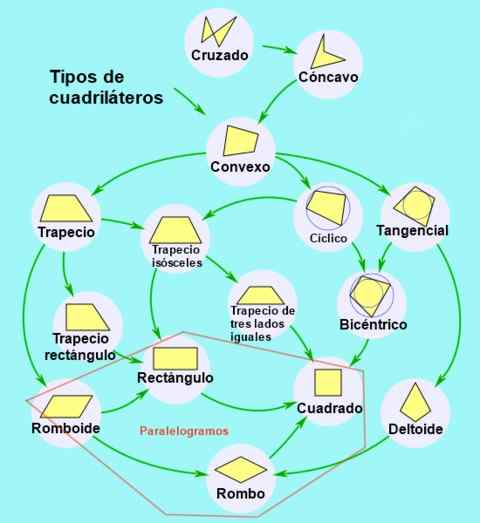Figur 2. Klassifisering og underklassifisering av kvadrilaterale. Kilde: Wikimedia Commons.

Typer parallellogram

På sin side kan parallellogrammer klassifiseres i henhold til deres vinkler og sider som følger:

1. Rektangel, Det er parallellogrammet som har sine fire interne vinkler med like mål. De indre vinklene til et rektangel danner en rett vinkel (90º).
2. Torget, Det er et rektangel med sine fire sider med like mål.
3. Diamant, Det er parallellogrammet med sine fire sider, men de forskjellige tilstøtende vinklene.
4. Rhomboid, parallellogram med forskjellige tilstøtende vinkler.

Trapes

Trapeze er en konveks firkantet med to parallelle sider.

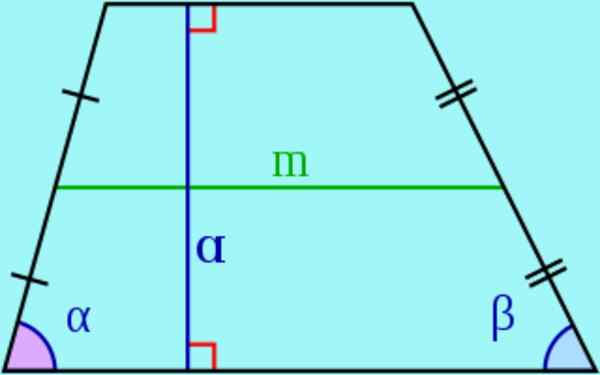Figur 3. Baser, lateral, høyde og median av en trapes. Kilde: Wikimedia Commons.

- I en trapes kalles parallelle sider baser Og ikke -parallellene kalles lateral.

- De høyde av en trapes er avstanden mellom de to basene, det vil si lengden på et segment med ender i basene og vinkelrett på den samme. Dette segmentet kalles også en trapeshøyde.

- De median Det er segmentet som blir med på midtpunktene på sidene. Det kan demonstreres at medianen er parallell med basene i trapesen og dens lengde er lik semi -kroppene til basene.

- Området til en trapes er høyden multiplisert med semi -kroppene til basene:

Område av en trapes = høyde * (base 1 + base 2) / 2

Typer trapes

-Rektangel trapes: Det er den som har en side vinkelrett på basene. Denne siden er også høyden på trapesiden.

-Trapezium isosceles: Den med like lengde sider. I en isosceles trapesid er vinklene ved siden av basene like.

-Escaleno Trapezio: Den som har sine sider av forskjellig lengde. De motsatte vinklene kan være akutte og den andre stump, men det kan også skje at begge er stump eller begge akutte.

Kan tjene deg: Løst faktoriseringsøvelser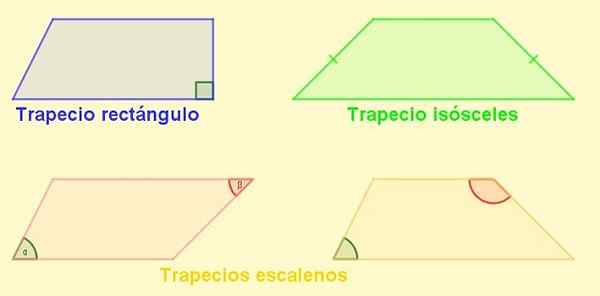 Figur 4. Typer trapes. Kilde: f. Zapata.

Parallellogram

Parallellogrammet er en firkantet hvis motsatte sider er parallelle to til to. I et parallellogram er de motsatte vinklene de samme, og de tilstøtende vinklene er supplerende, eller med andre ord, de tilstøtende vinklene totalt 180º.

Hvis et parallellogram har rett vinkel, vil alle andre vinkler også være, og den resulterende figuren kalles rektangel. Men hvis rektangelet også har sine tilstøtende sider av samme lengde, er alle sidene like, og den resulterende figuren er en torget.

Figur 5. Parallellogrammer. Rektangelet, firkanten og rhombus er parallellogrammer. Kilde: f. Zapata.

Når et parallellogram har to tilstøtende sider av samme lengde, vil alle sidene være av samme lengde, og det resulterende figur er en diamant.

Høyden på et parallellogram er et segment med ender på motsatte sider og vinkelrett på dem.

Et parallellogramområde

Området til et parallellogram er produktet av basen etter høyden, og basen er en side vinkelrett på høyden (figur 6).

Område av et parallellogram = base x høyde = a . h

Diagonaler av et parallellogram

Torget til diagonalen som starter fra et toppunkt er lik summen av rutene til de to sidene ved siden av nevnte toppunkt mer det doble produktet på disse sidene ved kosinus i vinkelen til det toppunktet:

F² = a² +  d² + 2 a d cos (α)

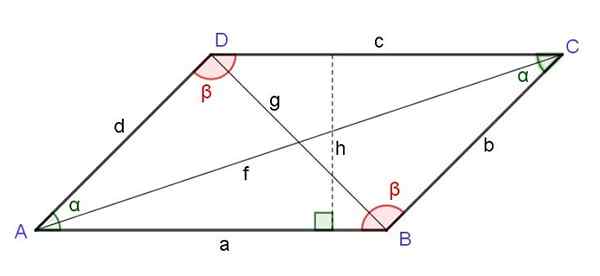Figur 6. Parallellogram. Motsatte vinkler, høyde, diagonaler. Kilde: f. Zapata.

Torget til diagonalen i motsetning til toppunktet til et parallellogram er lik summen av rutene til de to sidene ved siden av nevnte toppunkt og trakk det doble produktet fra disse sidene ved kosinus i vinkelen til den toppunktet:

g² = a² + d² - 2 a d cos (α)

Parallelograms lov

I et hvilket som helst parallellogram er summen av rutene på sidene lik summen av kvadratene til diagonalene:

til² + b² + c² + d² = f² + g²

Rectangle

Rektangelet er en firkantet med sine motsatte sider parallelle to til to, og det har også en rett vinkel. Det vil si at rektangelet er en type parallellogram med rett vinkel. For å være parallellogram, Rektangelet har sine motsatte sider av lik lengde A = C og B = D. 

Men som i ethvert parallellogram tilstøtende vinkler er supplerende og de like motsatte vinklene, i rektangelet ved å ha en rett vinkel, vil det nødvendigvis danne rette vinkler i de tre andre vinklene. Det er å si I et rektangel må alle indre vinkler mål 90º eller π/2 radianer.

Diagonaler av et rektangel

I et rektangel er diagonalene like lengde, Som vil bli demonstrert nedenfor. Resonnementet er som følger; Et rektangel er et parallellogram med alle dets rette vinkler, og det er grunnen til at det arver alle egenskapene til parallellogrammet, inkludert formelen som gir lengden på diagonalene:

F² = a²+  d² + 2 a d cos (α)

g² = a² + d² - 2 a d cos (α)

med α = 90º

Som Cos (90º) = 0, Så det hender at:

F² = g² = a² +  d²

Det er f = g, og derfor lengdene F og g Av de to diagonalene i rektangelet er de like, og lengden er gitt av:

Diagonal lengde på et rektangel = √ (a² + b²)

I tillegg, hvis det er i et rektangel på tilstøtende sider til og b Den ene siden er basert på den andre siden vil være høyde, og følgelig vil rektangelområdet være:

Det kan tjene deg: Fibonacci -serien: egenskaper, naturlige forhold, applikasjoner

Rektangelområde = a x b.

Omkretsen er summen av alle sider av rektangelet, men ettersom motsetningene er de samme, er det da nødvendig for et sider rektangel til og b Omkretsen er gitt av følgende formel:

Rektangelomkrets = 2 (A + B)

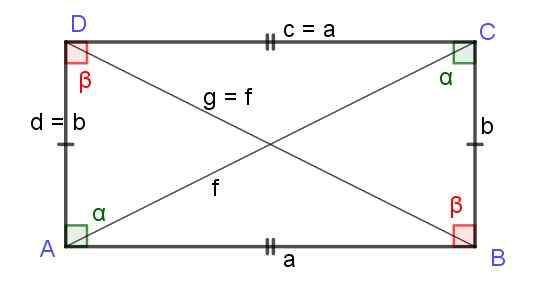Figur 7. Rektangel på sidene A og B. Diagonalene F og G er like lengde. Kilde: f. Zapata.

Torget

Torget er et rektangel med sine tilstøtende sider av samme lengde. Hvis torget har side til, Så diagonalene hans F og g De har samme lengde, som er F = g = (√2) a.

Området på et kvadrat er dens side hevet til torget:

Område av en firkant = a²

Omkretsen til en kvadrat er det dobbelte av siden:

Omkretsen av en kvadrat = 4 a

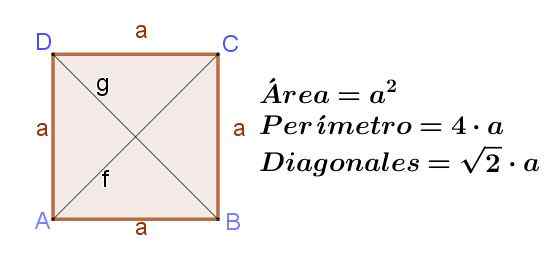Figur 8. Firkant til side A, som indikerer dets område, omkretsen og lengden på diagonalene. Kilde: f. Zapata ..

Diamant

Rhombus er et parallellogram med sine tilstøtende sider av samme lengde, men som i et parallellogram er de motsatte sidene de samme da, Alle sider av en rhombus er like lengde.

Diagonalene til en rhombus er av forskjellig lengde, men de er kuttet i rette vinkler.

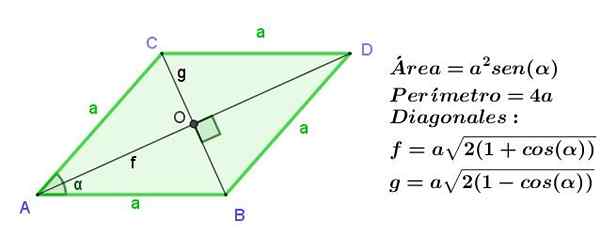Figur 9. Rhombus fra side A, som indikerer dets område, omkrets og lengden på diagonalene. Kilde: f. Zapata.

Eksempler

Eksempel 1

Demonstrer at de indre vinklene totalt i en firkantet (ikke krysset) totalt 360º (ikke krysset).

Figur 10: Det er demonstrert som summen av vinklene til en firkantet tilsett 360º. Kilde: f. Zapata.

ABCD regnes som en ABCD (se figur 10) og den diagonale BD er trukket. To ABD- og BCD -trekanter dannes. Summen av de indre vinklene til ABD -trekanten er:

α + β₁ + Δ₁ = 180º

Og summen av de interne vinklene til BCD -trekanten er:

 β2 + γ + Δ₂ = 180º

Å legge til de to ligningene oppnås:

α + β₁ + Δ₁ +  β₂ + γ + Δ₂ = 180º + 180º

Gruppering:

α + (β₁ +  β₂) + (Δ₁ + Δ₂) + γ = 2* 180º

Gruppering og renowing, blir det endelig demonstrert at:

α + β + Δ + γ = 360º

Eksempel 2

Demonstrer at medianen av en trapesoid er parallell med basene og dens lengde er semi -seismum av basene.

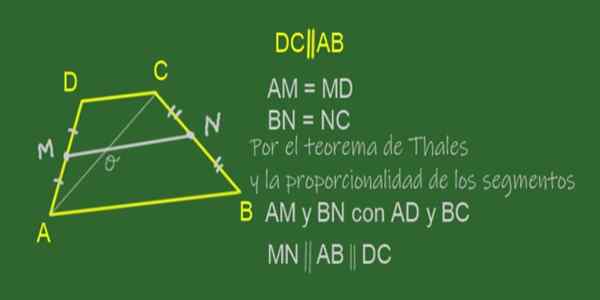Figur 11. Median MN av ABCD -trapesen. Kilde: f. Zapata.

Median av en trapes er segmentet som sammenføyer midtpunktene på sidene, det vil si de ikke -parallelle sidene. I ABCD -trapes vist i figur 11 er medianen MN. 

Fordi det er et midtpunkt for AD og N Mid BC Point, er det oppfylt at kvotientene AM / AD og BN / BC er like.

Det vil si at AM er proporsjonal med BN i samme andel som AD er BC, så betingelsene for anvendelse av teoremet (gjensidig) av Thales som bekrefter følgende:

""Hvis i tre eller flere rett kuttet med to secant"".

I vårt tilfelle er det konkludert med at MN-, AB- og DC -linjene er parallelle med hverandre, derfor:

“LI en median er en av en trapes parallelt med basene"".

Kan tjene deg: kombinert operasjoner

Nå vil Thales teorem gjelde:

""Et sett med paralleller kuttet av to eller flere tørking bestemmer proporsjonale segmenter"".

I vårt tilfelle AD = 2 am, AC = 2 AO, så DAC -trekanten ligner på Mao -trekanten, og følgelig DC = 2 mo.

Et lignende argument tillater å bekrefte at Cu ligner Con, der Ca = 2 CO og CB = 2 CN. Det følger at ab = 2 på.

Kort sagt, ab = 2 på y 2 mo. Så når vi har forlatt:

Ab + dc = 2 på + 2 mo = 2 (mo + på) = 2 mn

Endelig fjerner MN:

Mn = (ab + dc) /2

Og det konkluderes med at medianen til en trapesoid måler semi -kroppene til basene, eller med andre ord: medianen måler summen av basene, delt med to.

Eksempel 3

Demonstrer at i en rhombus er diagonalene kuttet i rette vinkler.

Figur 12. Rhombus og demonstrasjon av at diagonalene deres er kuttet i rette vinkler. Kilde: f. Zapata.

Styret i figur 12 viser nødvendig konstruksjon. Først er ABCD -parallellogrammet tegnet med AB = BC, det er en Rhombus. AC- og DB -diagonalene bestemmer åtte vinkler vist på figuren.

Ved hjelp av teoremet (a.Yo.p.) som sier at interne alternative vinkler mellom paralleller kuttet av en sekant bestemmer like vinkler, kan vi fastslå følgende:

α₁ = γ₁, α2 = γ2, Δ₁ = Β₁ og Δ2 = β2. (*)

På den annen side, ettersom de tilstøtende sidene av en rhombus er av like lengde, bestemmes fire isosceles -trekanter:

DAB, BCD, CDA og ABC

Nå påberopes trekanten teorem (isosceles) som sier at vinklene ved siden av basen er av like mål, hvor det konkluderes med at:

Δ₁ = β2, Δ2 = β₁, α2 = γ₁ og α₁ = γ2 (**)

Hvis forhold (*) og (**) er kombinert, oppnås neste likhet av vinkler:

α₁ = α2 = γ₁ = γ₁ På den ene siden og β₁ = Β2 = Δ₁ = Δ2 for den andre. 

Husker teoremet til de like trekantene som bekrefter at to trekanter med en like side mellom to like vinkler er de samme er:

AOD = AOB og følgelig også vinklene ∡Aod = ∡AOB.

Deretter ∡AOD + ∡AOB = 180º, men ettersom begge vinklene har like mål, 2 ∡AOD = 180º, noe som innebærer at ∡AOD = 90º.

Det vil si at det er geometrisk demonstrert at diagonalene til en rhombus kuttes i rette vinkler.

Øvelser løst

- Oppgave 1

Demonstrer at i et rektangel trapesidzoid, er ikke-EG-vinkler supplerende.

Løsning

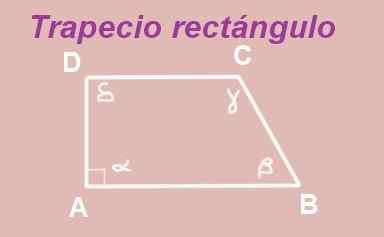Figur 13. Rektangel trapes. Kilde: f. Zapata.

ABCD Trapezoid er bygget med parallelle AB- og DC -baser. Den indre vinkelen til toppunktet A er rett (måler 90º), så du har et rektangel trapesidzoid.

Vinklene α og Δ er indre vinkler mellom to parallelle AB og DC -paralleller, derfor er de de samme, det vil si Δ = α = 90º. 

På den annen side er det vist at summen av de indre vinklene til en firkantet tilfører 360º, det vil si:

α + β + γ + Δ = 90º + β + 90º + Δ = 360º.

Ovennevnte fører til:

 β + Δ = 180º

Bekreftelse av hva som ønsket å bli demonstrert at vinklene β og Δ er supplerende.

- Oppgave 2

Et ABCD -parallellogram har AB = 2 cm og AD = 1 cm, i tillegg er vinkelen Bad 30º. Bestem området med nevnte parallellogram og lengden på de to diagonalene.

Løsning

Området til et parallellogram er produktet av lengden på basen etter høyde. I dette tilfellet vil lengden på segmentet B = AB = 2 cm bli tatt som en base, den andre siden har lengde A = AD = 1 cm og høyden H vil bli beregnet som følger:

H = annonse * sin (30º) = 1 cm * (1/2) = ½ cm.

Deretter: område = b * h = 2 cm * ½ cm = 1 cm².

Referanser

1. C. OG. TIL. (2003). Geometrielementer: med øvelser og kompassgeometri. University of Medellin.
2. Campos, f., Cerecedo, f. J. (2014). Matematikk 2. Patria redaksjonell gruppe.
3. Frigjort, k. (2007). Oppdag polygoner. Benchmark Education Company.
4. Hendrik, v. (2013). Generaliserte polygoner. Birkhäuser.
5. Iger. (s.F.). Matematikk første semester Tacaná. Iger.
6. JR. Geometri. (2014). Polygoner. Lulu Press, Inc.
7. Miller, Heeren, & Hornsby. (2006). Matematikk: Resonnement og applikasjoner (tiende utgave). Pearson Education.
8. Patiño, m. (2006). Matematikk 5. Redaksjonell progreso.
9. Wikipedia. Firedoblinger. Gjenopprettet fra: er.Wikipedia.com