Hva er delene av det kartesiske flyet?
- 3994
- 119
- Marius Aasen
De deler av det kartesiske flyet De er sammensatt av to virkelige, vinkelrett linjer, som deler det kartesiske planet i fire regioner. Hver av disse regionene kalles kvadranter og elementene i det kartesiske planet kalles punkter. Flyet, sammen med koordinataksene, kalles Kartesisk plan Til ære for den franske filosofen René Descartes, som oppfant analytisk geometri.
De to linjene (eller koordinataksene) er vinkelrett fordi de danner en vinkel på 90 º mellom dem og krysser til et felles punkt (opprinnelse). En av linjene er horisontalt, og blir kalt opprinnelse til X (eller ABCISA) og den andre linjen er vertikal, og blir kalt opprinnelse til y (eller bestilt).
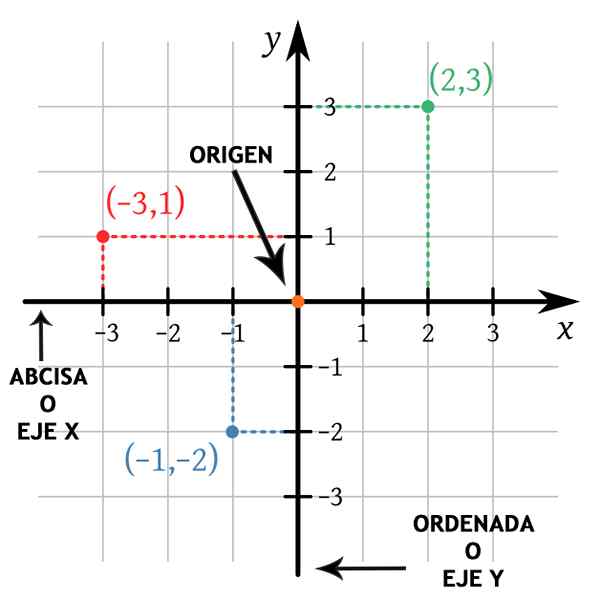 Kbolino / Public Domain
Kbolino / Public Domain Den positive halvparten av x -aksen er til høyre for opprinnelsen og den positive halvdelen av Y -aksen er oppe opprinnelsen. Dette gjør det mulig å skille de fire kvadrantene i det kartesiske planet som er veldig nyttig når du graferer punkter i flyet.
Kartesiske planpunkter
På hvert punkt P Flyet kan tilordnes et par reelle tall som er dets kartesiske koordinater.
Hvis en horisontal linje og en vertikal linje går gjennom P, Og du krysser hverandre ved x og aksen til y -aksen til og b henholdsvis, deretter koordinatene til P er (til,b). Det kalles til (til,b) Et ordnet par og rekkefølgen antallet er skrevet er viktig.
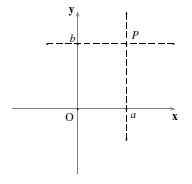
Det første nummeret, til, Det er koordinaten i "x" (eller abscissa) og det andre nummeret, b, Det er koordinaten i "y" (eller bestilt). Notasjon brukes P = (til,b).
Det er tydelig på den måten det kartesiske planet ble bygget at opprinnelsen tilsvarer “x” og 0 -aksen i “y” -aksen, det vil si, ENTEN= (0,0).
Cuadies av det kartesiske flyet
Som det fremgår av de tidligere figurene, genererer koordinataksene fire forskjellige regioner som er kvadrantene i det kartesiske planet, som er betegnet med bokstavene og, II, iii og IV Og disse skiller seg fra hverandre i tegnet om at punktene som er i hver av dem har.
Kan tjene deg: algebraisk resonnementKvadrant Yo
Poengene til kvadranten Yo De er de som begge har koordinater med et positivt tegn, det vil si deres X -koordinat og deres koordinat og er positive.
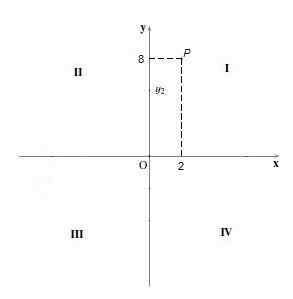
For eksempel poenget P = (2.8). For å tegne det, er punkt 2 plassert på “X” -aksen og punktet 8 på “Y” -aksen, deretter trekkes de vertikale og horisontale linjene, og hvor de krysser er der punktet er P.
Kvadrant Ii
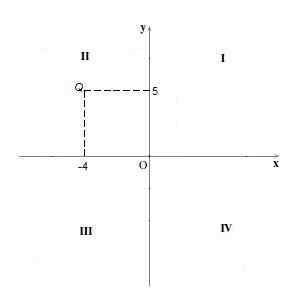
Poengene til kvadranten Ii De har sin negative "X" -koordinat og den positive "y" -koordinaten. For eksempel poenget Q = (-4.5). Det er grafisk prosedyre som i forrige tilfelle.
Kvadrant Iii
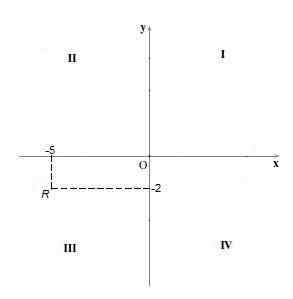
I denne kvadranten er tegnet på begge koordinatene negativt, det vil si koordinaten "x" og koordinaten "y" besittelse er negativ. For eksempel punkt r = (-5, -2).
Kvadrant IV
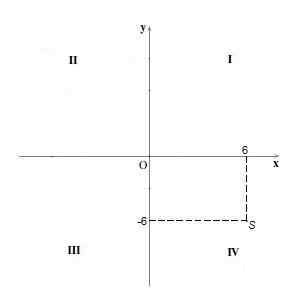
I kvadranten IV Poengene har en positiv og koordinat "y" negativ koordinering. For eksempel poenget S = (6, -6).

Referanser
- Fleming, w., & Varberg, D. (1991). Algebra og trigonometri med analytisk geometri. Pearson Education.
- Larson, r. (2010). Prealculus (8 utg.). Cengage Learning.
- Lojal, j. M., & Viloria, n. G. (2005). Flat analytisk geometri. Mérida - Venezuela: Venezuelansk redaksjon C. TIL.
- Oteyza, e. (2005). Analytisk geometri (Second Ed.). (G. T. Mendoza, red.) Pearson Education.
- Oteyza, e. d., Osnaya, e. L., Garciadiego, ca. H., Hoyo, a. M., & Flores, til. R. (2001). Analytisk geometri og trigonometri (First Ed.). Pearson Education.
- Purcell, e. J., Varberg, d., & Rigdon, s. OG. (2007). Beregning (Niende utg.). Prentice Hall.
- Scott, c. TIL. (2009). Cartesian Plane Geometry, Part: Analytical Conics (1907) (Reprint Ed.). Lynkilde.
- « De 5 mest fremragende språkvariasjonene
- Didaktiske intervensjonsegenskaper, strategier, eksempler »

