Hvor mye er x av x?

Å multiplisere x av x du får x².

x² leser som "X kvadrat"Eller ganske enkelt"X kvadrat"".

Hvorfor x av x er x²?

Resultatet av x av x er x².

Det er et veldig enkelt resultat å bekrefte, takket være Eiendom av multiplikasjonen av krefter med lik base.

I algebra brukes bokstaven X som en måte å kalle et beløp som tar ukjente verdier, selv om andre bokstaver også kan brukes.

Eiendommen til multiplikasjonen av krefter fra samme base sier at "Når du multipliserer to identiske baser, er den samme basen skrevet og eksponentene blir lagt til"".

x^til∙ x^b = x^A+b

Eksponenten lik 1 av X er vanligvis utelatt, slik at x¹ = x.

Hvis vi vil vite hvor mye x av x:

De base er x (det samme er skrevet) og Eksponenter legges til+B (Verdiene er lik 1):

x ∙ x = x¹⁺¹ = x²

Eksempler på eiendommen til multiplikasjonen av krefter med lik base

La oss se på noen veldig enkle numeriske eksempler:

2 × 2 = 2² = 4

3 × 3 = 3² = 9

4 × 4 = 4² = 16

(−2) × (−2) = 2² = 4

Merk at det negative tegnet over ikke endrer resultatet, siden i henhold til loven om tegn, multipliserer to negative mengder positivt resultat.

I de foregående eksemplene ble hele tall brukt, men operasjonen er like gyldig for desimal, brøk, reelle og komplekse tall.

Området på en firkant

Torget til et tall vises ofte i beregningen av områder med vanlige geometriske figurer. For eksempel den til torget, som er en enkelt firet polygon, som alle har samme mål.

Kan tjene deg: System of Equations: Solution Methods, Eksempler, øvelser

Området på et kvadrat er gitt av kvadratet på siden, hvis det kalles “x”, så er området A på torget verdt x².

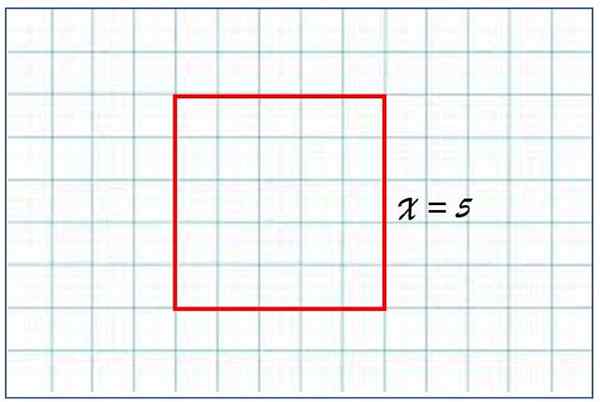
Eksempel på området på et kvadrat

Firkantet område A hvis side er x = 5 enheter er lik:

A = 5² = 5 × 5 = 25 enheter

En firkant på siden lik 5 vilkårlige enheter med lengde har et område på 25 enheter med areal. Kilde: f. Zapata.

Dette resultatet er fornuftig, siden kvadratet består av 5 rader og 5 søyler med mindre firkanter, fra siden lik 1. Hvis leseren observerer figuren nøye, vil han innse at det røde torget består av 25 små firkanter med enhetlig område.

Viktig:

Enhetene i dette eksemplet er vilkårlige, de kan være meter, centimeter, tommer eller annet. Her ble de ikke spesifisert, men i alle fall ville det respektive området bli gitt i meter kvadratiske, kvadratiske, kvadratmeter eller andre. Området er alltid gitt i enheter med kvadratlengde.

Kvadratet med brøk- og desimaltall

For å finne kvadratet med et brøknummer, som er et som består av en nummerert og en nevner, atskilt med brøkdelen, er det nødvendig å multiplisere telleren med seg selv, så vel som nevneren, og få et nytt brøknummer.

Eksempler på firkantede tall

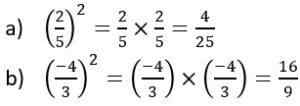
Eksempler på kvadratmeter

Når det gjelder kvadratet med et desimaltall, må vi følge multiplikasjonsreglene for desimaltall.

a) 0.6² = 0.6 × 0.6 = 0.36

b) (−0.4)² = (−0.4) × (−0.4) = 0.16

Både i dette eksemplet og den tilsvarende en av forrige seksjon observeres det at kvadratet med et negativt tall alltid er positivt. Dette gjelder for de jevne kreftene, ikke bare for torget.

Kan tjene deg: tilsvarende sett: Hva er, forklaring, eksempler