Avkoding av uttrykk
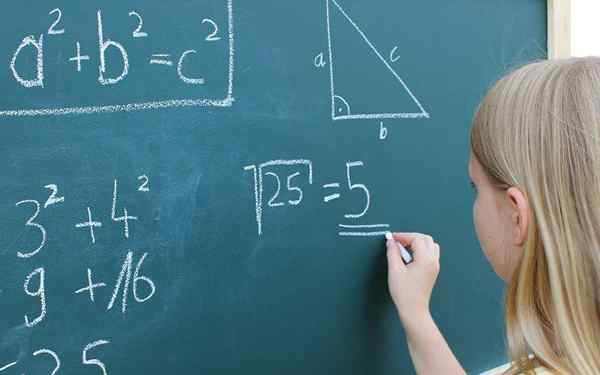
- 1836
- 333
- Daniel Skuterud
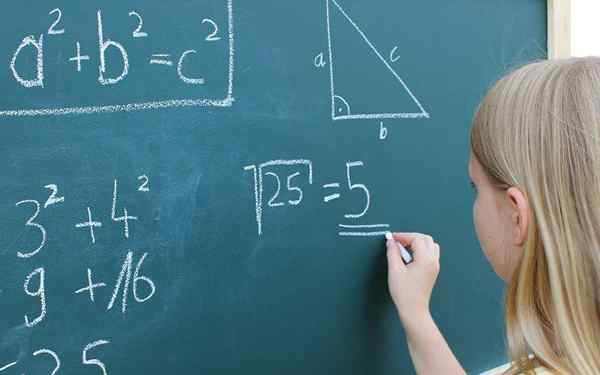 Matematiske uttrykk. Med lisens
Matematiske uttrykk. Med lisens Hva er avkoding av uttrykk?
De Avkoding av uttrykk Det refererer til måten å muntlig uttrykke et matematisk uttrykk. I matematikk, a uttrykk, Også kalt matematisk uttrykk, det er en kombinasjon av bokstavelige koeffisienter og bokstavelige deler gjennom andre matematiske tegn (+, -, x, ±, /, [],), for å danne en matematisk operasjon.
Med enklere ord er koeffisientene representert med tall, mens den bokstavelige delen består av bokstaver (de tre første bokstavene i alfabetet, A, B og C, brukes vanligvis til å utpeke den bokstavelige delen).
På sin side representerer disse "bokstavene" størrelser, variabler og konstanter som en numerisk verdi kan tilordnes.
Matematiske uttrykk består av begreper, som er hvert av elementene som er atskilt med operasjonssymboler. For eksempel har følgende matematiske uttrykk fire begreper:
5x2 + 10x + 2x + 4
Det skal bemerkes at uttrykk bare kan utgjøres av koeffisienter, av koeffisienter og bokstavelige deler og bare av bokstavelige deler.
For eksempel:
25 + 12
2x + 2y (algebraisk uttrykk)
3x + 4/y + 3 (irrasjonell algebraisk uttrykk)
x + y (hele algebraisk uttrykk)
4x + 2y2 (Hele algebraisk uttrykk)
Avkoding av matematiske uttrykk
Avkoding av enkle matematiske uttrykk
1. A + B: Summen av to tall
For eksempel: 2 + 2: summen av to og to
2. A + b + c: summen av tre tall
For eksempel: 1 + 2 + 3: summen av en, to og tre
3. A - B: Subtraksjonen (eller forskjellen) på to tall
For eksempel: 2 - 2: subtraksjonen (eller forskjellen) på to og to
4. A X B: Produktet av to tall
Kan tjene deg: problemtilnærmingFor eksempel: 2 x 2: produktet av to og to
5. til ÷ B: De to tallforholdet
For eksempel: 2/2: kvotienten til to og to
6. 2 (x): To ganger et tall
For eksempel: 2 (23): To ganger 23
7. 3 (x): trippel av et tall
For eksempel: 3 (23): trippel av 23
8. 2 (A + B): Det dobbelte av summen av to tall
For eksempel: 2 (5 + 3): Det dobbelte av summen av fem og tre
9. 3 (A + B + C): Trippel av summen av tre tall
For eksempel: 3 (1 + 2 + 3): trippel av summen av en, to og tre
10. 2 (A - B): Det dobbelte av forskjellen på to tall
For eksempel: 2 (1 - 2): dobbelt så
elleve. X/2: Halvparten av et tall
For eksempel: 4/2: halvparten av fire
12. 2n + x: summen av dobbelt ett tall og et annet tall
For eksempel: 2 (3) + 5: Summen av dobbelt tre og fem
1. 3. X> y: "equis" er større enn "dere"
For eksempel: 3> 1: tre er større enn en
14. x < y: “Equis” es menor que “ye”
For eksempel: 1 < 3: Uno es menor que tres
femten. X = y: "equis" er lik "dere"
For eksempel: 2 x 2 = 4: Produktet av to og to er lik fire
16. x2 : Kvadratet med et tall eller et kvadratnummer
For eksempel: 52 : Den fem eller fem kvadratkoble
17. x3: Kuben til et tall eller et tall til kuben
For eksempel: 53: Fem eller fem kube til kuben
Kan tjene deg: kvalitativ metode18. (A + B)2: Kvadratet med summen av to tall
For eksempel: (1 + 2)2: Kvadratet med summen av en og to
19. (x - y)/2: Halvparten av forskjellen på to tall
For eksempel: (2 - 5)/2: Halvparten av forskjellen på to og fem
tjue. 3 (x + y)2: Trippel av kvadratet av summen av to tall
For eksempel: 3 (2 + 5)2 : Trippel kvadratet av summen av to og fem
tjueen. (A + B)/2: To tall
For eksempel: (2 + 5)/2: den to -og fem semi -serismum
Avkoding av algebraiske uttrykk
1. 2 x5 + 7/y + 9: [to equis hevet til fem] flere [syv over dere] mer [ni]
2. 9 x + 7y + 3 x6 - 8 x3 + 4 y: [ni equis] mer [syv år] mer [tre equis hevet til seks] mindre [åtte equis hevet til 3] mer [fire år]
3. 2x + 2y: [to equis] mer [to år]
4. X/2 - y5 + 4y5 + 2x2: [x på 2] mindre [og hevet til fem] flere [fire og hevet til fem] flere [to kvadratmet hevet]
5. 5/2 x + y2 + x: [fem på to equis] mer [og kvadrat] mer [equis]
Polynomisk avkoding
1. 2x4 + 3x3 + 5x2 + 8x + 3: [to av equis hevet til de fire] flere [tre av equis hevet til de tre] flere [fem av torget forhøyet] mer [8 av equis] pluss tre
2. 13 og6 + 7y4 + 9y3 + 5y: [Tretten av og hevet til seks] Mer [syv av og hevet til de fire] flere [ni av og hevet til de tre] flere [fem av dere]]
3. 12Z8 - 5z6 + 7z5 + z4 - 4Z3 + 3Z2 + 9Z: [Tolv av zeta hevet til åtte] mindre [fem av zeta hevet til seks] mer [syv av zeta hevet til fem] mer [Zeta hevet til fire] minus [fire av Zeta hevet til kuben] mer [tre av zeta forhøyet til torget] mer [ni av Zeta]
Det kan tjene deg: Matematikkens betydning for å adressere fysiske situasjonerReferanser
- Krøllete uttrykk med variabler. Gjenopprettet fra Khanacademy.org.
- Forståelse av algebraiske uttrykk fra erfarne brukere av matematikk. NCBI kom seg.NLM.NIH.Gov.
- Skrive matematiske uttrykk. Gjenopprettet fra Mathgoodies.com.

