Algebraiske derivater

Hva er algebraiske derivater?

De algebraiske derivater De består av studiet av derivatet i det spesielle tilfellet av algebraiske funksjoner. Opprinnelsen til forestillingen om derivat stammer tilbake til det gamle Hellas. Utviklingen av denne forestillingen ble motivert av behovet for å løse to viktige problemer, en i fysikk og en i matematikk.

I fysikk løser derivatet problemet med å bestemme den øyeblikkelige hastigheten til et bevegelig objekt. I matematikk tillater det å finne tangentlinjen til en kurve på et gitt punkt.

Selv om det egentlig er mange flere problemer som løses ved å bruke derivatet, så vel som dens generaliseringer, ble resultater som kom senere til introduksjonen av deres konsept.

Pioneers of Differential Calculus er Newton og Leibniz. Før vi gir den formelle definisjonen, vil vi utvikle ideen bak, fra det matematiske og fysiske synspunktet.

Derivatet som i påvente av tangentlinjen til en kurve

Anta at grafen til en y = f (x) -funksjon er en kontinuerlig graf (uten pigger eller toppunkter eller separasjoner), og enten a = (a, f (a)) et fast punkt over det. Vi ønsker å finne tangentlinjeligningen til funksjonen f på punkt a.

La oss ta et annet punkt p = (x, f (x)) av grafen, nær punkt A, og spore tørkelinjen som passerer gjennom A og P. En tørkelinje er en linje som skjærer til grafen til en kurve i ett eller flere punkter.

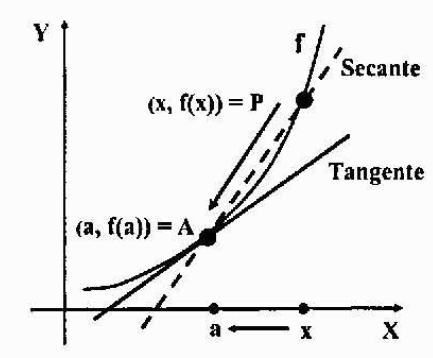
For å få tangenslinjen vi ønsker, er det bare nødvendig å beregne skråningen fordi vi allerede har et punkt på linjen: punktet a.

Hvis vi flytter punktet P med grafen og vi nærmer oss det mer og mer til punkt A, vil den tidligere nevnte tørre linjen nærme seg tangentlinjen du vil finne. Å ta grensen når "P har en tendens til en", begge linjene vil sammenfalle, derfor også skråningene deres.

Hellingen på Secant -linjen er gitt av

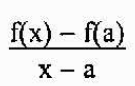
Å si at P er nær A, tilsvarer å si at "X" nærmer seg "A". Dermed vil skråningen av tangentlinjen til grafen til F på punkt A være lik:

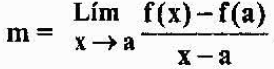
Det forrige uttrykket er betegnet med f '(a), og er definert som derivatet av en funksjon f på punktet "a". Vi ser at analytisk, derivatet av en funksjon på et punkt er en grense, men geometrisk er det skråningen til linjens tangent til diagrammet for funksjonen på punktet.

Kan tjene deg: tilfeldig variabel: konsept, typer, eksempler

Nå vil vi se denne forestillingen fra fysikkens synspunkt. Vi vil nå det samme uttrykket av den forrige grensen, selv om det er en annen vei, og dermed oppnå enstemmigheten i definisjonen.

Derivatet som øyeblikkelig hastighet på et bevegelig objekt

La oss se på et kort eksempel på hva øyeblikkelig hastighet betyr. Når det for eksempel sies at en bil for å nå en destinasjon gjorde det med en hastighet på 100 km i timen, er det det betyr at han om en time reiste 100 km.

Dette betyr ikke nødvendigvis at bilen i løpet av hele timen alltid var 100 km. Hvis han hadde behov for å stå ved et trafikklys, var hastigheten i det øyeblikket 0 km. Etter en time var ruten imidlertid 100 km.

Dette er det som er kjent som gjennomsnittshastighet og er gitt av kvotienten til avstanden som er tilbakelagt mellom tiden som ble gått, som vi nettopp har sett. Den øyeblikkelige hastigheten er i mellomtiden den som markerer velocimeter nålen til en bil på et bestemt øyeblikk (tid).

La oss se dette nå mer generell måte. Anta at et objekt beveger seg langs en linje og at denne forskyvningen er representert ved hjelp av ligningen s = f (t), der variabelen t måler tiden og variabelen s forskyvningen, under hensyntagen til sin begynnelse i øyeblikket t = 0, da det også er null, det vil si F (0) = 0.

Denne funksjonen f (t) er kjent som posisjonsfunksjon.

Et uttrykk for objektets øyeblikkelige hastighet blir søkt på et fast øyeblikk. I denne hastigheten vil vi betegne det med V (a).

Det være seg ethvert øyeblikk nær øyeblikkelig "a". I tidsintervallet mellom “a” og “t” er endringen av posisjonen gitt av f (t) -f (a).

Gjennomsnittshastigheten i dette tidsintervallet er:

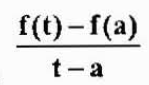
Som er en tilnærming av øyeblikkelig hastighet v (a). Denne tilnærmingen vil være bedre etter hvert som T kommer nærmere "A". Derfor,

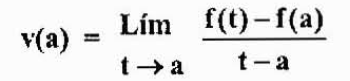
La oss legge merke til at dette uttrykket er lik det som er oppnådd i forrige tilfelle, men fra et annet perspektiv. Dette er det som er kjent som derivatet av en F -funksjon på et punkt "A" og er betegnet med F '(A), som angitt ovenfor.

Kan tjene deg: Eksponentlover

Merk at det å gjøre endringen h

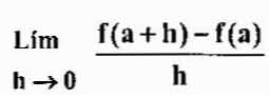
Begge uttrykkene er likeverdige, men noen ganger bør det brukes mer til den ene i stedet for den andre, avhengig av saken.

Det er da definert mer generelt som avledet fra en funksjon f når som helst "x" som tilhører dens domene som

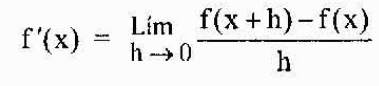
Den mest vanlige notasjonen for å representere derivatet av en funksjon y = f (x) er den vi nettopp har sett (f 'o y'). En annen mye brukt notasjon er imidlertid notasjonen til Leibniz som er representert som noen av følgende uttrykk:

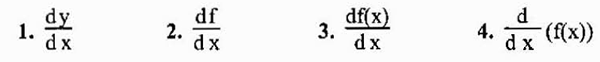
Med tanke på det faktum at derivatet i hovedsak er en grense, kan det hende at det ikke eksisterer, siden grensene ikke alltid eksisterer. I tilfelle det eksisterer, sies det at den aktuelle funksjonen er differensierbar på det gitte punktet.

Algebraisk funksjon

En algebraisk funksjon er en kombinasjon av polynomer gjennom summer, subtraksjoner, produkter, kvotienter, krefter og radikaler.

Et polynom er et uttrykk for form

P_n= a_nxⁿ+ til_N-1x^N-1+ til_N-2x^N-2+… + A₂x²+ til₁x+a₀

Hvor n er et naturlig tall og alt_Yo, Med i = 0,1, ... er n rasjonelle tall og_n≠ 0. I dette tilfellet sies det at graden av dette polynomet er n.

Følgende er eksempler på algebraiske funksjoner:

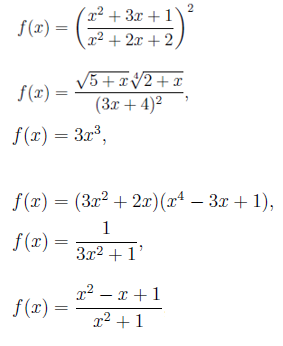
Her er ikke eksponentielle, logaritmiske og trigonometriske funksjoner inkludert. Avledningsreglene som vi vil se nedenfor er gyldige for funksjoner generelt, men vi vil begrense og anvende dem i tilfelle algebraiske funksjoner.

Derrying regler

Avledet fra en konstant

Sier at derivatet av en konstant er null. Det vil si hvis f (x) = c, så f '(x) = 0. For eksempel er derivatet av konstant funksjon 2 lik 0.

Avledet fra en makt

Hvis f (x) = xⁿ, deretter f '(x) = nx^N-1. For eksempel x derivat³ Det er 3x². Som en konsekvens av dette oppnås det at avledet fra identitetsfunksjonen f (x) = x er f '(x) = 1x^1-1= x⁰= 1.

Et annet eksempel er som følger: la f (x) = 1/x², deretter f (x) = x^-2 og f '(x) = -2x^-2-1= -2x^-3.

Denne egenskapen er også gyldige røtter, ettersom røttene er rasjonelle krefter og ovennevnte også kan brukes i så fall. For eksempel er avledet fra en kvadratrot gitt av

Det kan tjene deg: estimering etter intervaller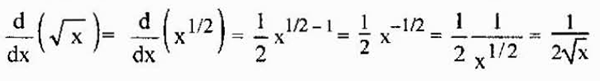

Avledet fra en sum og en subtraksjon

Hvis f og g er differensierbare funksjoner i x, er summen f+g også, og det er oppfylt at (f+g) '(x) = f' (x)+g '(x) (x) (x).

Tilsvarende må du (f -g) '(x) = f' (x) -g '(x). Med andre ord, derivatet av en sum (subtraksjon) er summen (eller subtraksjon) av derivater.

Eksempel

Hvis h (x) = x²+X-1, da

H '(x) = (x²)+(x) '-(1)' = 2x+1-0 = 2x+1.

Produkt avledet fra et produkt

Hvis F og G er differensierbare funksjoner i X, er FG -produktet også differensierbar i X, og det er oppfylt at

(fg) '(x) = f' (x) g (x)+f (x) g '(x).

Som en konsekvens har det hvis C er en konstant og F er en differensiell funksjon i X, da er CF også differensierbar i X Y (CF) '(X) = CF' (X).

Eksempel

Hvis f (x) = 3x (x²+1), da

f '(x) = (3x)' (x²+1)+(3x) (x²+1) '= 3 (x)' (x²+1)+3x [(x²) '+(1)]

= 3 (1) (x²+1)+3x [(2x^2-1) +0] = 3 (x²+1)+3x (2x) = 3x²+3+6x²

= 9x²+3.

Avledet fra en kvotient

Hvis f og g er differensierbare i x og g (x) ≠ 0, er f/g også differensierbar i x, og det er oppfylt at

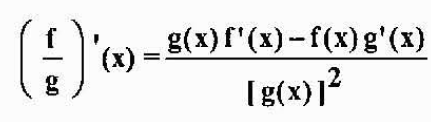
Eksempel: Hvis h (x) = x³/(x²-5x), da

H '(x) = [(x³) '(X⁵-5x)-(x³) (x⁵-5x) ']/ (x⁵-5x)²= [(3x²) (x⁵-5x)- (x³) (5x⁴-5)]/ (x⁵-5x)².

Kjedestyre

Denne regelen gjør det mulig å utlede sammensetningen av funksjoner. Den fastslår følgende: Hvis y = f (u) er differensierbar i u, og u = g (x) er differensierbar i x, er den sammensatte funksjonen f (g (x)) differensierbar i x, og det er oppfylt at [F (F (F (F (F (F (F (F (F (F (F (F (F (F (F (F (F (F (F (F (F (F G (x))] '= f' (g (x)) g '(x).

Det vil si at derivatet av en sammensatt funksjon er produktet av derivatet av den eksterne funksjonen (eksternt derivat) av den interne funksjonen avledet (internt derivat).

Eksempel

Hvis f (x) = (x⁴-2x)³, så

f '(x) = 3 (x⁴-2x)²(x⁴-2x) '= 3 (x⁴-2x)²(4x³-2).

Det er også resultater for å beregne det omvendte derivatet av en funksjon, så vel som generaliseringen til derivater av høyere orden. Søknader er omfattende. Blant dem blir fortjenesten deres i optimalisering og minimumsfunksjoner fremhevet.

Referanser

1. Alarcon, s., González, m., & Quintana, h. (2008). Differensiell beregning. Itm.
2. Cabrera, v. M. (1997). 4000 beregning. Redaksjonell progreso.
3. Castaño, h. F. (2005). Matematikk før beregning. University of Medellin.
4. Eduardo, n. TIL. (2003). Introduksjon til beregning. Umbrale utgaver.
5. Kilder, a. (2016). Grunnleggende matematikk. En introduksjon til beregning. Lulu.com.
6. Purcell, e. J., Rigdon, s. OG., & Varberg, D. OG. (2007). Beregning. Pearson Education.
7. Saenz, J. (2005). Differensiell beregning (Second Ed.). Barquisimeto: Hypotenusa.
8. Thomas, g. B., & Weir, m. D. (2006). Beregning: Flere variabler. Pearson Education.