Diameter symboler og formler, hvordan du tar det ut, omkrets

Han diameter Det er den rette linjen som passerer gjennom midten av en lukket flat kurve eller en figur i to eller tre dimensjoner, og som også blir med på de motsatte punktene. Det er vanligvis en sirkel (en flat kurve), en sirkel (en flat figur), en sfære eller en rett sirkulær sylinder (tre -dimensjonale gjenstander).

Selv om omkrets og sirkel vanligvis tas som synonymer, er det en forskjell mellom begge begrepene. Omkretsen er den lukkede kurven som omslutter sirkelen, som oppfyller betingelsen om at avstanden mellom noen av punktene og senteret er den samme. Denne avstanden er ingen ringere enn omkretsens radius. I stedet er sirkelen en flat figur begrenset av omkretsen.

Figur 1. Diameteren på sykkelhjulene er en viktig funksjon i designen. Kilde: Pixabay.

Ved omkrets, sirkel og sfære er diameteren et rett segment som inneholder minst tre punkter: sentrum pluss to punkter på kanten av omkretsen eller sirkelen, eller overflaten på sfæren.

Og når det gjelder den rette sirkulære sylinderen, refererer diameteren til tverrsnittet, som sammen med høyden er dens to karakteristiske parametere.

Diameteren på omkretsen og sirkelen, symbolisert av Ø eller ganske enkelt bokstaven "D" eller "D", er relatert til dens omkrets, kontur eller lengde, som er betegnet med bokstaven L:

L = π.D = π. enten

Hver gang du har en omkrets, er kvotienten mellom dens lengde og diameter det irrasjonelle tallet π = 3.14159 ..., på denne måten:

π = l/d

[TOC]

Hvordan få diameteren?

Når tegningen av omkretsen eller sirkelen er tilgjengelig, eller direkte det sirkulære objektet, for eksempel en valuta eller en ring for eksempel, er det veldig enkelt å ta diameteren med en regel. Du må ganske enkelt sørge for at kanten av regelen samtidig har to punkter i omkretsen og sentrum av det samme.

Kan tjene deg: algebraic

Et kaliber, vernier eller kongens fot er veldig egnet for å måle ytre og indre diametre i mynter, bøyler, ringer, nøtter, rør og mer.

Figur 2. Vernier digital måle diameteren til en mynt. Kilde: Pixabay.

Hvis du i stedet for objektet eller tegningen har data som radioen R, Deretter multipliserer du diameteren. Og hvis omkretsens lengde eller omkrets er kjent, kan diameteren også være kjent, ved klarering:

D = 2.R
D = l / π

En annen måte å få diameter er å kjenne sirkelområdet, den sfæriske overflaten, tverrsnittet av sylinderen, det buede området til dette eller volumene på sfæren eller sylinderen. Alt avhenger av hvilken geometrisk figur som er det. For eksempel er diameteren involvert i følgende områder og volumer:

-Sirkelområde: π.(D/2)²
-Sfærisk overflate: 4π.(D/2)²
-Sfærevolum: (4/3) π.(D/2)³
-Rett sirkulær sylindervolum: π.(D/2)².H (H er sylinderhøyden)

Tall med konstant bred

Sirkelen er en flat figur med konstant bred, siden uansett hvor den ser ut, er bredden diameter d. Imidlertid er det andre kanskje mindre kjente figurer hvis bredde også er konstant.

La oss først se hva som forstås med bredde på en figur: det er avstanden mellom to parallelle linjer -støtte Remes -, som igjen er vinkelrett på den gitte retningen og som fengsler figuren, som vist i venstre bilde:

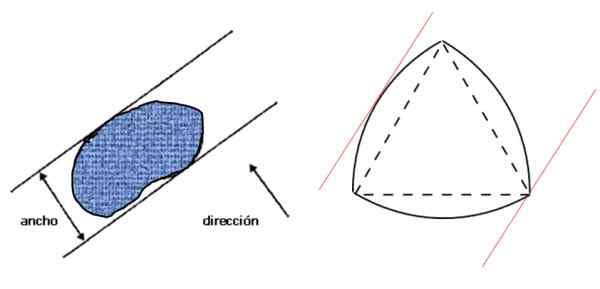Figur 3. Bredde på en hvilken som helst flat figur (til venstre) og Reuleaux -trekant, en konstant bred figur (til høyre). Kilde: f. Zapata.

Så til høyre er Reuleaux -trekanten, som er en konstant bred figur og som oppfyller tilstanden som er spesifisert i venstre figur. Hvis bredden på figuren er D, er omkretsen gitt av Barbiers teorem:

Kan tjene deg: Omtrentlig måling av amorfe figurer: Eksempel og trening

L = π.D

Kloakkene i byen San Francisco i California er formet som Reuleaux's Triangle, kalt av den tyske ingeniøren Franz Reuleaux (1829 - 1905). På denne måten kan ikke tapasene falle nedover hullet og bruke mindre materiale for å produsere dem, fordi området deres er mindre enn sirkelen:

A = (1- √3).πd² = 0.705.D²

Mens for en sirkel:

A = π.(D/2)² = (π/4) D²= 0.785.D²

Men denne trekanten er ikke den eneste konstante brede figuren. Samtaler kan bygges Reuleaux polygoner med andre polygoner som har et merkelig sidetall.

Diameter på en omkrets

I neste figur er elementene i omkretsen, definert som følger:

Tau: linjesegment som blir med to punkter i omkretsen. I figuren er tauet som sammenføyer punktene C og D, men uendelige strenger kan spores som unike et par punkter i omkretsen.

Diameter: Det er tauet som passerer gjennom sentrum, og blir sammen med to punkter i omkretsen med sentrum eller. Det er det lengste tauet av en omkrets, av den grunn kalles det "Major Rope".

Radio: linjesegment som blir med i sentrum med et hvilket som helst punkt i omkretsen. Verdien, som diameteren, er konstant.

Omkrets: Det er settet med alle punkter som likestiller eller.

Bue: Det er definert som et omkretssegment avgrenset av to radioer (ikke tegnet i figuren).

Figur 4. Deler av omkretsen, inkludert diameteren, som passerer gjennom sentrum. Kilde: Wikimedia Commons.

- Eksempel 1

Rektangelet som vises måler 10 tommer høyt, som når den vikler det, danner en rett sirkulær sylinder hvis diameter er 5 tommer. Svar på følgende spørsmål:

Det kan tjene deg: gjensidig utelukkende hendelser: egenskaper og eksempler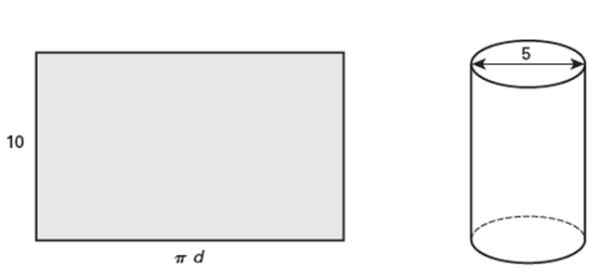Figur 5. Et rullet rektangel blir en rett sirkulær sylinder. Kilde: Jiménez, R. Matematikk II. Geometri og trigonometri. 2. Utgave. Pearson.

a) Hva er konturen til røret?
b) Finn rektangelområdet
c) Beregn kors -avsnittsarealet til sylinderen.

Løsning på

Konturen til røret er l = π.D = 5π plg = 15.71 plg.

Løsning b

Rektangelområdet er Base x høyde, Å være basen L som allerede er beregnet og høyden er 10 PLG i henhold til uttalelsen, derfor:

A = 15.71 PLG x 10 PLG = 157.1 plg².

Løsning c

Til slutt beregnes det forespurte området som følger:

A = π.(D/2)² = (π/4) D² = (π/4) x (5 plg)²= 19.63 plg².

- Eksempel 2

Beregn det skyggelagte området i figur 5a. Torget har side l.

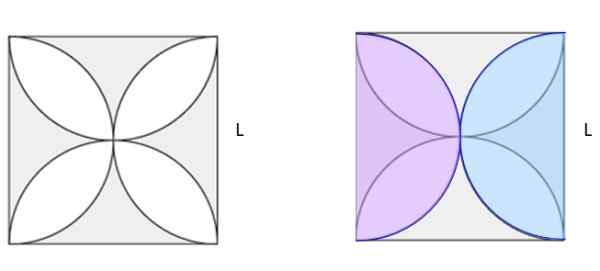Figur 6. Finn det skyggelagte området i venstre figur. Jiménez, r. Matematikk II. Geometri og trigonometri. 2. Utgave. Pearson.

Løsning

I figur 5b er det tegnet to identiske høysirkler av størrelse i rosa og blå farger, overlagret på den opprinnelige figuren. Mellom dem lager de en komplett sirkel. Hvis kvadratet på torget beregnes og sirkelområdet trekkes fra, gjør det det skyggelagte området i figur 5b. Og ser bra ut, det viser seg at det er halvparten av det skyggelagte området i 5A.

-Area Square: L²
-Semi -sirkel diameter: l
-Sirkelområde: π.(L/2)²= (π/4) l²
-Forskjell på områder = halvparten av det skyggelagte området =

L² - (π/4) l² = [(4 - π)/4] l²= 0.2146 l²

-Skyggelagt område = 2 x 0.2146 l²= 0.4292L2

Hvor mange diametre har en omkrets?

Uendelige diametre kan trekkes i en sirkel, og noen av dem måler det samme.

Referanser

1. Antonio. Reuleaux -trekanter og andre konstant bredde kurver. Gjenopprettet fra: Disseminatorer.com.
2. Baldor, a. 2002. Flat og rom og trigonometri geometri. Kulturell hjemlandsgruppe.
3. Jiménez, r. Matematikk II. Geometri og trigonometri. 2. Utgave. Pearson.
4. Wikipedia. Reuleaux Triangle. Gjenopprettet fra: det er.Wikipedia.org.
5. Wolfram Mathworld. Diameter. Gjenopprettet fra: Mathworld.Wolfram.com.