Frekvensfordeling hvordan lage et bord, eksempel, trening

EN Frekvensfordeling I statistikk refererer det til trenden som følger dataene som er organisert i grupper, kategorier eller klasser, når hver og en blir tildelt et nummer som kalles frekvens, noe som indikerer hvor mange data det er i hver gruppe. 

Som regel observeres det at disse frekvensene er fordelt rundt en sentral gruppe: den med det høyeste antallet data.

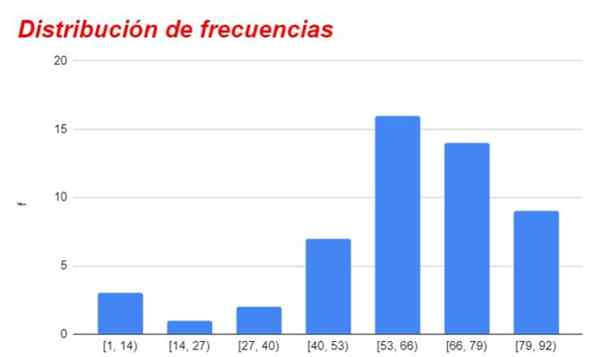
Figur 1. Frekvensfordelingsdiagram hentet fra det tilsvarende tabellen. Kilde: f. Zapata.

Grupper som er over eller under nevnte sentralkategori reduserer gradvis frekvensen, og er veldig liten eller ubetydelig for kategoriene lengst fra kategorien med høyere frekvens.

Måten å kjenne frekvensfordelingen til et datasett består først av å lage kategoriene og deretter lage frekvenstabellen. Den visuelle representasjonen av frekvenstabellen kalles histogram.

[TOC]

Frekvenstyper

Det er flere typer frekvenser:

1.- Absolutt fresuens: Det er det mest grunnleggende, og fra det er de andre bygget. Det består ganske enkelt av det totale antallet data som tilsvarer en kategori.

2.- Relativ frekvens: Det er den absolutte frekvensen for hver kategori delt på det totale antallet data.

3.- Prosentvis frekvens: Det er den samme relative frekvensen, men multiplisert med hundre, noe som indikerer prosentandelen av verdiene i hver kategori.

4.- Akkumulert frekvens: Det er summen av de absolutte frekvensene for kategoriene lavere eller lik kategorien som blir vurdert. 

5.- Prosentandel akkumulert frekvens: Det er summen av prosentvis frekvenser for kategoriene lavere eller lik kategorien som blir observert.

Trinn for å lage en frekvensfordelingstabell

Det er flere trinn som skal følges for å bygge en frekvensfordelingstabell.

For det første må dataene til et tre osv.

Kan tjene deg: hva er delingene av 30? (Forklaring)

Trinn 1

Identifiser minimumsverdien Xmin og maksimal verdi Xmax I datasettet x.

Steg 2

Beregn R -området, som er definert som forskjellen mellom maksimalverdien mindre minimumsverdien: r = xmax - xmin.

Trinn 3

Bestem nummeret k av intervaller eller klasser, som kan være forhåndsopprettet. Antallet k vil bestemme antall rader som frekvensbordet vil ha.

Trinn 4

I tilfelle antall intervaller k Det er ikke tidligere gitt, da må det etableres i henhold til følgende retningslinjer: det minste antall anbefalte kategorier er 5, men det kan være høyere i hvilket tilfelle det er å foretrekke å velge et oddetall.

Trinn 5

Det er en formel som heter Sturges regel Det gir oss antall intervaller k anbefalt for et sett som består av N data:

K = [1 + 3.322⋅log n]

Ettersom resultatet innen braketten sikkert vil være et reelt tall, indikerer braketten at den må avrundes til det nærmeste rare heltallet for å oppnå en heltallverdi på k.

Trinn 6

Amplituden beregnes TIL av hvert intervall (klasser eller kategorier) som tar kvotienten mellom området R og antall intervaller k: A = r/k. Hvis de opprinnelige dataene er hele tall, er det nærmeste heltallet avrundet, ellers er dens virkelige verdi igjen.

Trinn 7

Bestem de nedre og øvre grensene for hvert intervall eller klasse. Det første intervallet, eller den laveste klassen, har som sin nedre grense den minste av de opprinnelige dataene, det vil si Li = Xmin og som den øvre begrensningen minimumsverdien pluss amplituden til intervallet, er dette LS = XMIN + A. 

Trinn 8

De påfølgende intervallene er: 

[Xmin, xmin + a), [ Xmin + a, xmin + 2⋅a), ... [ Xmin + (k-1) a, xmin + k⋅a).

Kan tjene deg: kombinert operasjoner

Trinn 9

XC -klassemerket er bestemt for hvert intervall, ved å bruke følgende formel: Xc = (ls - li) / 2 + li.

Trinn 10

Overskriften på frekvensbordet er plassert, som består av en rad med følgende etiketter: klasser, XC -klassemerke, frekvens F, relativ frekvens F (eller prosentvis frekvens F%) og akkumulert frekvens F (eller akkumulert prosentfrekvens F%).

Det vi vil ha neste gang er følgende:

Første kolonne i frekvensbordet: inneholder intervallene eller klassene som dataene er blitt delt.

Andre kolonne: Inneholder klassemerket (eller mellompunktet) for hvert underintervall.

Tredje kolonne: Inneholder den absolutte frekvensen F for hver klasse eller kategori.

Fjerde og femte kolonne: Verdiene som tilsvarer den relative (eller prosentandelen) frekvensen og den akkumulerte frekvensen F (eller prosentandelen akkumulert) er plassert.

Tabellkonstruksjonseksempel

Følgende data tilsvarer de nøyaktige svarene på 100 spørsmål som brukes til en gruppe på 52 studenter:

65, 70, 70, 74, 61, 77, 85, 36, 70, 62, 62, 77, 80, 89, 39, 43, 70, 77, 79, 77, 88, 52, 85, 1, 55, 55, 47, 73, 63, 59, 51, 56, 65, 85, 79, 53, 79, 3, 71, 7, 54, 8, 61, 61, 77, 67, 58, 61, 45, 48, 64, 15, 50.

Vi vil følge trinnene for å bygge frekvensbordet:

1.- Minimums- og maksimumsverdier XMin = 1, Xmax = 89.

2.- Området er: r = 89 - 1 = 88

3.- Bestemmelse av antall intervaller i henhold til Sturges regel: K = [1 + 3,322⋅log 52] = [6,70] = 7.

4.- Beregning av bredden på intervallene: a = r / k = 88/7 = 12,57 ≈ 13.

5.- Intervallene er: [1,14), [14, 27), [27, 40), [40, 53), [53, 66), [66, 79), [79, 92).

6.- Klassemerkene i hvert intervall bestemmes: 8, 21, 34, 47, 60, 73 og 86.

7.- Bordet er laget:

Kan tjene deg: interne og eksterne konjugatvinkler: eksempler, øvelser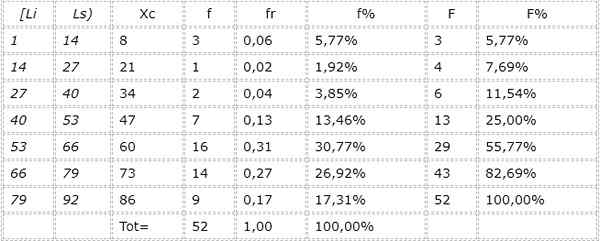

Grafen over frekvensene for de forskjellige intervallene eller kategoriene er vist i figur 1.

Trening løst

En lærer registrerer prosentandelen av mål oppnådd i emnet fysikk for hver elev. Kvalifiseringen til hver student, selv om det avhenger av prosentandelen av målene som oppnådde, er imidlertid tett til visse kategorier som tidligere er etablert i universitetsstudierforskriften.

La oss se på et spesifikt tilfelle: I en fysikkseksjon har du prosentandelen av mål oppnådd for hver av de 52 studentene: 

15, 50, 62, 58, 51, 61, 62, 74, 65, 79, 59, 56, 77, 8, 55, 70, 7, 36, 79, 61, 77, 52, 35, 43, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61. 65, 70, 89, 64, 54, 85, 61, 39, 63, 70, 85, 70, 79, 48, 77, 73, 67, 45, 77, 71, 53, 88, 85, 47, 73, 77, 80.

I dette eksemplet tilsvarer kategoriene eller klassene den endelige kvalifiseringen som er tildelt i henhold til prosentandelen X for oppnådd mål:

1.- Veldig dårlig: 1 ≤ x < 30

2.- Dårlig: 30 ≤ x < 50

3.- Nok: 50 ≤ x < 70

4.- Vel: 70 ≤ x < 85

5.- Utmerket: 85 ≤ x ≤ 100

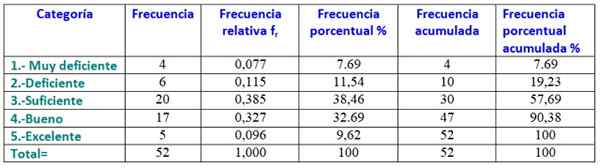
For å lage frekvenstabellen bestilles dataene fra minst til størst og forteller hvor mange data som tilsvarer hver kategori, noe som vil være den kvalifiseringen som studenten vil få i emnet fysikk:

1.- Veldig dårlig: 4 studenter.

2.- Dårlig: 6 studenter.

3.- Nok: 20 studenter.

4.- Vel: 17 studenter.

5.- Utmerket: 5 studenter.

Nedenfor er histogrammet over karakterer, bygget fra forrige tabell:

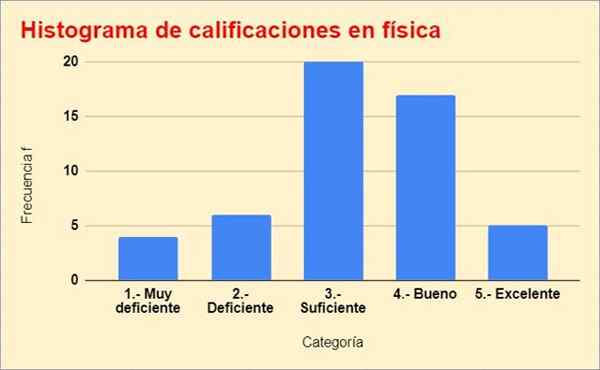Figur 2. Frekvensfordelingsgrafen for øvelsen løst. Kilde: f. Zapata.

Referanser

1. Berenson, m. 1985. Statistikk for administrasjon og økonomi. Inter -American s.TIL.
2. Canavos, g. 1988. Sannsynlighet og statistikk: applikasjoner og metoder. McGraw Hill.
3. Devore, J. 2012. Sannsynlighet og statistikk for ingeniørfag og vitenskap. 8. Utgave. Cengage.
4. Levin, r. 1988. Statistikk for administratorer. 2. Utgave. Prentice Hall.
5. Spiegel, m. 2009. Statistikk. Schaum -serien. 4 ta. Utgave. McGraw Hill.
6. Walpole, r. 2007. Sannsynlighet og statistikk for ingeniørfag og vitenskap. Pearson.