Fourier Series -applikasjoner, eksempler og øvelser løst

De Fourier -serien De består av en sum av uendelige termer, som består av harmoniske funksjoner, bihule og kosinus, hvis argument er et helt grunnleggende av en grunnleggende frekvens.

Sinus- og kosinusfunksjonene multipliseres med verdikoeffisienter, slik at summen er identisk med en funksjon med periode T lik to ganger Pi (2π) delt på den grunnleggende vinkelfrekvensen ω ω.

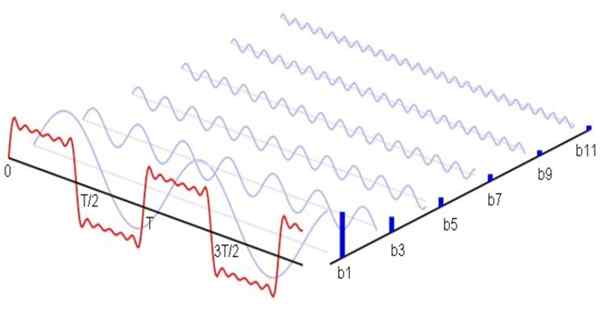
Figur 1. Her er (i blått) den første ikke -NULL -harmonikken i Fourier -serien som tilsvarer et firkantet bølgeformsignal. Summen disse harmonikkene gir det røde signalet Røde signal. Kilde: Wikimedia Commons.

Matematisk vil det bli uttrykt som følger: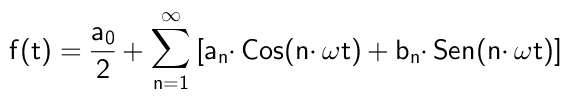

Hvor Ω Det er den grunnleggende frekvensen, som er relatert til perioden T av funksjonen f (t) Gjennom forholdet: 

Ω = 2π / t

For å være periodisk periode T, funksjonen f (t) oppfyller denne tilstanden:

f (t) = f (t + k t)

Hvor k Det er et heltall og koeffisientene til₀ , til_n og b_n De kalles Fourier koeffisienter.

[TOC]

Betydning og bruk av Fourier -serien

Navnet på Fourier -serien skyldes at oppdageren hans var den franske matematiske.

Denne oppdagelsen var grunnleggende for matematikk, siden hvis en differensialligning har en spesiell harmonisk løsning, er det mulig å oppnå den generelle løsningen ved hjelp av overlappingen eller summen av det samme.

Fouriers koeffisienter av en periodisk funksjon, også kalt skilt, De er spekteret av det samme.

Derfor er spekteret settet med frekvenser som utgjør et signal preget av amplituden til hver frekvens, som tilsvarer verdiene til Fouriers koeffisienter.

Signalkompresjonssystemer eller lyd- og videobølgeformer, i ryggen betydelig mindre antall biter enn det originale digitaliserte signalet.

Fourier -serien med et signal er som fingeravtrykket, i den forstand at du, kjent koeffisientene som utgjør det, alltid kan vite hvilket tegn de tilhører.

Selv om bruken av Fourier -serien, eller dens mest generelle form, Fourier Transform, Som en signalkompresjonsmetode har det vært kjent i ganske lang tid, bruken i praksis måtte vente på numeriske prosessorer raskt nok, som gjorde at signalene ble komprimert og dekomprimert i "sanntid".

Kan tjene deg: statistiske variabler

Fourier Series -eksempel 

Deretter et eksempel på F (t) funksjon og dens Fourier -serie.

Funksjonen er:

 f (t) = 0 ja 0 ≤ t  < π y 1 si π ≤  t   < 2π

Og har den tilsvarende Fourier -serien gitt av:

f (t) = ½ - 2/π⋅se (t) - 2/(3π) ⋅se (3t) - 2/(5π) ⋅sen (5t) - 2/(7π) ⋅sen (7t) - ..

Følgende figur viser funksjonen og delvis summen av Fourier -serien:

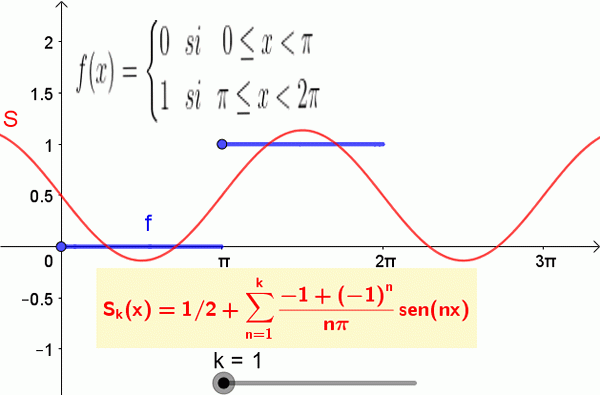Figur 2. De første 19 vilkårene i Fouriers sum som tilsvarer trinnfunksjonen er vist. Kilde: f. Zapata.

Bestemmelse av koeffisienter

Nedenfor er hvordan du bestemmer Fouriers koeffisienter:

Anta at funksjonen er f (x) definert i et intervall som går fra t_Yo til T_Yo + T, der kapital vil være perioden for funksjonen. Da er Fourier -serien hans:

f (t) = a₀/2 + a₁ cos (ω t) + a₂ cos (2 Ω t) +… + a_n Cos (n ω t) +..

.. .+ b₁ sin (ω t) +b₂ sin (2 Ω t) +… +b_n Sin (n ω t) +..

Beregning av det uavhengige begrepet

For å finne det uavhengige begrepet integrerer vi begge medlemmer av likhet i intervallet av definisjonen av funksjonen:

[t_Yo , t_Yo+ T]

Derfor:

Samme_n ∫cos (n ω t) dt +..

.. .+ b₁ ∫sen (ω t) dt +b₂ ∫sen (2 Ω t) dt +… +b_n ∫sen (n ω t) dt +..

Her symbolet ∫ betyr integrert definert fra t_Yo til T_Yo + T.

Integralen av det første begrepet er T, som når den blir evaluert i den øvre grenseresultatet:

t_Yo + T

Når du trekker ned den nedre grensen t_Yo, i definitiv t.

Alle andre vilkår er 0, fordi dette er kosinus- eller bihulefunksjoner evaluert i en hel periode, som vi viser nedenfor:

∫cos (nω t) dt = (1/ nω) ∫cos (nω t) d (nω t)

Husk at symbolet ∫ betyr integrering mellom t_Yo til T_Yo + T. 

For å gjøre integrasjonen av begrepene som har kosinus eller bryst, vil vi gjøre følgende variabelendring:

x = ω (t - t_Yo)

Så x, dx differensial er lik D (ωt) differensialet.

Så integralen som skal utføres er:

Ettersom n er et heltall, vil den definerte integralen alltid gi null. Det samme gjelder sinusfunksjonen.

Derfor inneholder den definerte integralen evaluert i en fullstendig periode av alle vilkårene. 

Kan tjene deg: divisjoner der resten er 300

Det konkluderes derfor med at begrepet A₀ beregnes som følger:

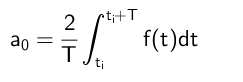
Beregning av koeffisienter til

For å beregne koeffisientene til som multipliserer til kosinusfunksjonene, må begge medlemmer av likhet multipliseres:

f (t) = a₀/2 + a₁ cos (ω t) + a₂ cos (2 Ω t) +… + a_n Cos (n ω t) +..

.. .+ b₁ sin (ω t) +b₂ sin (2 Ω t) +… +b_n Sin (n ω t) +..

Av kosinusfunksjonen evaluert i den tilsvarende harmoniske og deretter integralet som er definert i en full periode til begge medlemmene, blir brukt. 

For eksempel å beregne_m Begge medlemmene multipliseres med COS (Mωt):

f (t) cos (m ω t) = a₀/2 cos (m ω t) + a₁ cos (ω t) cos (m ω t) + a₂ cos (2 ω t) cos (m ω t) + ... + + til_n Cos (n ω t) cos (m ω t) +..

.. .+ b₁ sin (ω t) cos (m ω t) +b₂ sin (2 ω t) cos (m ω t) +… +b_n Sin (n ω t) cos (m ω t) +..

Integrer deretter i en komplett periode, det vil si i intervallet som går fra t_Yo til T_Yo + T.

Integralen av begrepet som inneholder A₀ kanselleres, fordi M er et heltall og kosinusfunksjonen blir integrert i en full periode. 

Integraler som inneholder produktet cos (n ω t) cos (m ω t) er også annullert når n ≠ m. Bare i tilfelle at n = m har integralet:

Alle begrepene som har en kosinus multiplisert bihule, det vil si de som multipliseres med Bs koeffisienter, som inneholdende integraler av SEN -typen (n ω t) cos (m ω t) blir kansellert når den definerte integralen gjøres på en komplett periode. 

Herfra er det konkludert med at:

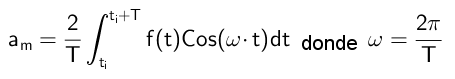
Beregning av koeffisientene B -er

For å finne Bs koeffisienter blir en lignende prosedyre brukt, men denne gangen multipliseres begge medlemmene av funksjonen til Fourier -serien med SEN -funksjonen (M ω T).

Av de samme grunnene som allerede er forklart for saken der det eneste begrepet som ikke er annullert etter å ha integrert seg i en komplett periode, er en der:

n = m

Og hvor integralen av [sen (m ω t)] vises]², som integrert på en fullstendig periode resulterer i π.

Kan tjene deg: Homografisk funksjon: Hvordan graf, løste øvelser

På denne måten beregnes Bs koeffisienter i henhold til følgende formel:

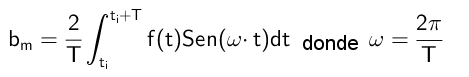
Øvelser

- Oppgave 1

Gjør den eksplisitte beregningen av funksjonens koeffisienter

 f (t) = 0 ja 0 ≤ t  < π y 1 si π ≤  t   < 2π

Løsning

Først identifiserer vi perioden T for denne funksjonen som 2π, så den grunnleggende frekvensen ω = 2π/ t i dette eksemplet er lik enheten, det vil si:

Ω = 1

Funksjonen er definert i intervallet [0, 2π], så alle integrasjoner vil bli utført i nevnte intervall. 

Da beregnes det uavhengige uttrykket som følger:

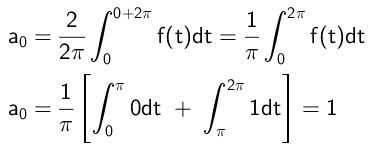
Koeffisientene som multipliserer til kosinusfunksjonene, beregnes på denne måten:

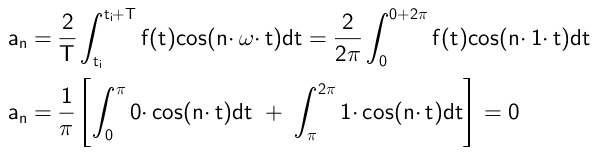
Som det kan sees, er alle koeffisienter til null, noe som vil skje, forutsatt at funksjonen f (t) er merkelig.

Tilsvarende vil Bs koeffisienter bli beregnet som følger:

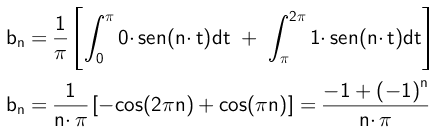
- Oppgave 2

Finn koeffisientene til funksjonen som tilsvarer figur 1, som er:

f (t) = -1 ja 0≤ t

Løsning 

Ettersom funksjonen tar verdier mellom -1 og +1, kan vi intuitere at det uavhengige uttrykket er ugyldig, men vi vil eksplisitt beregne det:

På grunn av det faktum at funksjonen har merkelig symmetri, må alle koeffisienter til å multiplisere de harmoniske begrepene med kosinusfunksjonen være ugyldig. Vi bekrefter det nedenfor:

Til slutt vil vi finne Bs koeffisienter som multipliserer de harmoniske begrepene som inneholder bihulefunksjonen:

Hvor kan alle Bs vilkår med UP -abonnement bli lagt merke til er 0. De første rare begrepene er:

b₁= -4/(π); b₃= -4/(3π); b₅= -4/(5π); b₇= -4/(7π) og b₉= -4/(9π)

https: // youtu.Være/737yagwszya

Referanser

1. Aminror, i. 2013. Å mestre den diskrete Fourier -transformasjonen i en, to eller flere dimensjoner: fallgruver og gjenstander. Springer Science & Business Media.
2. Briggs, w. nitten nitti fem. DFT: En eierhåndbok for den diskrete Fourier -transformasjonen. Siam.
3. Chu, e. 2008. Diskrete og kontinuerlige Fourier -transformasjoner: Analyse, applikasjoner og raske algoritmer. CRC Press.
4. Guoan Bi, Yonghong Zeng. 2012. Transforms og raske algoritmer for signalanalyse og representasjoner. Springer Science & Business Media.
5. Sundararajan, d. 2003. Digital signalbehandling: teori og praksis.Verdens vitenskapelig. 
6. Wikipedia. Fourier -serien. Gjenopprettet fra: er.Wikipedia.com