Normal formelfordeling, egenskaper, eksempel, trening

De normal distribusjon o Gaussisk distribusjon er sannsynlighetsfordelingen i kontinuerlig variabel, der sannsynlighetstetthetsfunksjonen er beskrevet ved en eksponentiell funksjon av kvadratisk og negativt argument, noe som resulterer i en fliset form.

Det normale distribusjonsnavnet kommer fra det faktum at denne distribusjonen er den som brukes på det største antall situasjoner der noen kontinuerlige tilfeldige variabler er involvert i en gitt gruppe eller befolkning.

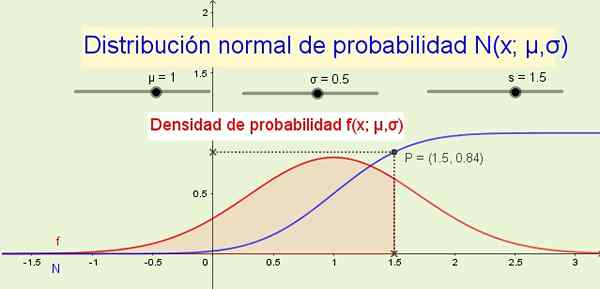
Figur 1. Normal distribusjon N (x; μ, σ) og dens sannsynlighetstetthet f (s; μ, σ). (Egen utdyping)

Som eksempler der normalfordeling brukes: Høyden på menn eller kvinner, varianter i en viss fysisk størrelse eller i målbare psykologiske eller sosiologiske trekk som den intellektuelle kvotienten eller forbruksvanene til et bestemt produkt.

På den annen side kalles det Gaussisk distribusjon eller Gauss Bell, fordi det er dette tyske matematiske geniet som blir kreditert med oppdagelsen for bruken han ga for beskrivelsen av den statistiske feilen i astronomiske målinger tilbake i 1800.

Imidlertid hevdes det at denne statistiske fordelingen tidligere ble publisert av en annen stor matematiker av fransk opprinnelse, som Abraham de Moivre, tilbake i 1733.

[TOC]

Formel

Til normalfordelingsfunksjonen i den kontinuerlige variabelen x, Med parametere μ og σ Det er betegnet med:

N (x; μ, σ)

Og eksplisitt er det skrevet slik:

N (x; μ, σ) = ∫_-∞^x f (s; μ, σ) ds

hvor f (u; μ, σ) Det er sannsynlighetstetthetsfunksjonen:

f (s; μ, σ) = (1/(σ√ (2π)) exp ( - s²/(2σ²)

Konstanten som multipliserer eksponentiell funksjon i sannsynlighetstetthetsfunksjonen kalles normaliseringskonstant, og er valgt på en slik måte at:

N (+∞, μ, σ) = 1

Det forrige uttrykket sikrer at sannsynligheten for at den tilfeldige variabelen x være mellom -∞ og +∞ enten 1, det er 100% sannsynlighet.

Parameteren μ Det er det aritmetiske gjennomsnittet av den kontinuerlige tilfeldige variabelen x og σ Standardavviket eller kvadratroten til variansen til den samme variabelen. I tilfelle det μ = 0 og σ = 1 Du har normal standard eller normal distribusjonsfordeling typisk: 

N (x; μ = 0, σ = 1)

Normale distribusjonsegenskaper

1- Hvis en tilfeldig statistisk variabel følger en normal sannsynlighetstetthetsfordeling f (s; μ, σ), De fleste dataene er gruppert rundt gjennomsnittsverdien μ Og de er spredt rundt dem slik at like over dataene er mellom μ - σ og μ + σ. 

Kan tjene deg: Absolutt frekvens: Formel, beregning, distribusjon, eksempel

2- Standardavviket σ Det er alltid positivt.

3- Formen for tetthetsfunksjonen F Det ligner den fra en bjelle, så denne funksjonen kalles ofte Gaussian Bell eller Gaussisk funksjon. 

4- I en gaussisk distribusjon er gjennomsnittlig median og mote sammenfaller.

5- Bøyningspunktene for sannsynlighetstetthetsfunksjonen finnes nøyaktig i μ - σ og μ + σ.

6- F-funksjonen er symmetrisk med hensyn til en akse som går etter gjennomsnittsverdien μ Og du har null asymptotisk for x ⟶ +∞ og x ⟶ -∞.

7- En høyere verdi av σ Større spredning, støy eller distansering av data rundt gjennomsnittsverdien. Det vil si til større σ Klokkeformen er mer åpen. I stedet σ Liten indikerer at terningene svømte til gjennomsnittet og formen på klokken er mer lukket eller spiss.

8- Distribusjonsfunksjonen N (x; μ, σ) indikerer sannsynligheten for at den tilfeldige variabelen er mindre enn eller lik x. For eksempel i figur 1 (over) sannsynligheten P at variabelen x er mindre enn eller lik 1.5 er 84% og tilsvarer området under sannsynlighetstetthetsfunksjonen f (x; μ, σ) Fra -∞ til x.

Tillitsintervaller

9- Hvis dataene følger en normalfordeling, er 68,26% av disse mellom μ - σ og μ + σ.

10- 95,44% av dataene som følger en normalfordeling er mellom μ - 2σ og μ + 2σ.

11- 99,74% av dataene som følger en normalfordeling er mellom μ - 3σ og μ + 3σ.

12- Hvis en tilfeldig variabel x Følg en distribusjon N (x; μ, σ), Deretter variabelen

Z = (x - μ) / σ  Følg standard normalfordeling  N (z; 0.1).

Endringen av variabelen x til z Det kalles standardisering eller typifisering og er veldig nyttig på tidspunktet for å bruke standardfordelingstabellene på data som følger en normal ikke-standardfordeling.

Normale distribusjonsapplikasjoner

For å anvende normalfordelingen er det nødvendig å gå gjennom beregningen av integralen av sannsynlighetstettheten, som fra det analytiske synspunktet ikke er lett og ikke alltid er tilgjengelig et dataprogram som tillater dets numeriske beregning. For dette formål brukes standard- eller karakteriserte verditabeller, noe som ikke er mer enn normalfordelingen i saken μ = 0 og σ = 1.

Kan tjene deg: kombinert operasjoner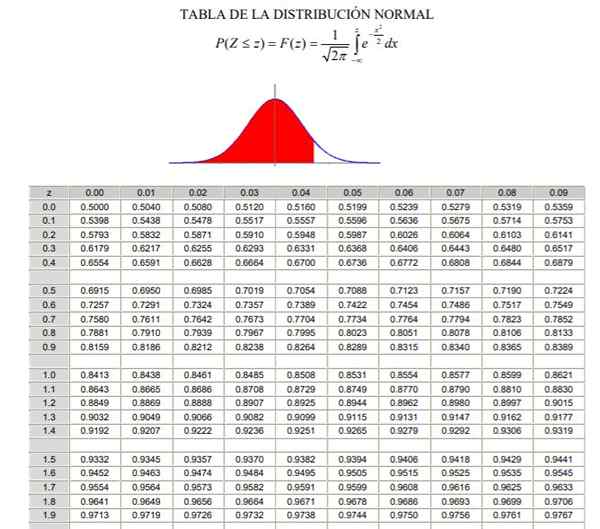Normal distribusjonstabell karakterisert (del 1/2) 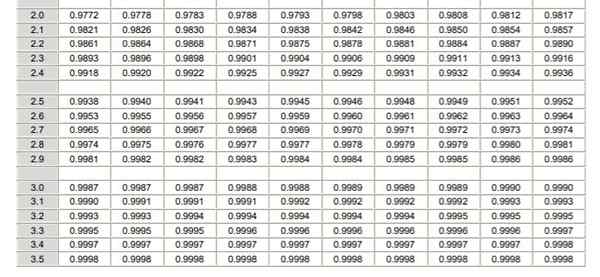Normal distribusjonstabell karakterisert (del 2/2)

Det skal bemerkes at disse tabellene ikke inkluderer negative verdier. Imidlertid ved å bruke symmetriegenskapene til den gaussiske sannsynlighetstetthetsfunksjonen, kan de tilsvarende verdiene oppnås. I den løste øvelsen vist nedenfor er bruken av tabellen indikert i disse tilfellene.

Eksempel

Anta at du har et tilfeldig datasett X som følger en normal gjennomsnittlig fordeling på 10 og standardavvik 2. Det blir bedt om å finne sannsynligheten for at:

a) Den tilfeldige variabelen x er mindre enn eller lik 8.

b) er mindre enn eller lik 10.

c) at variabel x er under 12.

d) Sannsynligheten for at en x -verdi er mellom 8 og 12.

Løsning:

a) For å svare på det første spørsmålet du bare må beregne:

N (x; μ, σ)

Med x = 8, μ = 10 og σ = 2. Vi innser at det er et integrert Erf (x).

På den annen side er det muligheten for å løse integralen på en numerisk måte, og det er det mange kalkulatorer, regneark og dataprogrammer som Geogebra gjør. Følgende figur viser den numeriske løsningen som tilsvarer det første tilfellet:

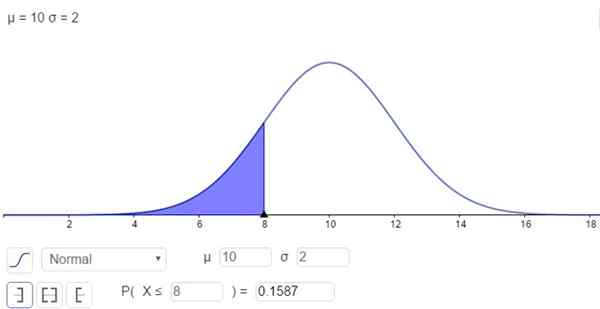Figur 2. Sannsynlighetstetthet f (x; μ, σ). Det skyggelagte området representerer P (x ≤ 8). (Egen utdyping)

Og svaret er at sannsynligheten for at X er under 8 er:

P (x ≤ 8) = n (x = 8; μ = 10, σ = 2) = 0.1587

b) I dette tilfellet handler det om å finne sannsynligheten for at den tilfeldige variabelen X er under gjennomsnittet at i dette tilfellet er verdt 10. Svaret krever ingen beregninger, siden vi vet at halvparten av dataene er under gjennomsnittet og den andre halvparten over gjennomsnittet. Derfor er svaret:

P (x ≤ 10) = n (x = 10; μ = 10, σ = 2) = 0,5

c) For å svare på dette spørsmålet må du beregne N (x = 12; μ = 10, σ = 2), som kan gjøres med en kalkulator som har statistiske funksjoner eller ved programvare som Geogebra:

Kan tjene deg: Divisors of 8: Hva er og enkel forklaring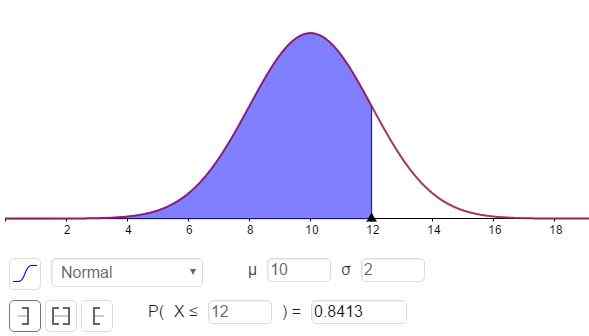Figur 3. Sannsynlighetstetthet f (x; μ, σ). Det skyggelagte området representerer P (x ≤ 12). (Egen utdyping)

Responsen på del C kan sees i figur 3 og er:

P (x ≤ 12) = n (x = 12; μ = 10, σ = 2) = 0,8413.

d) For å finne sannsynligheten for at den tilfeldige variabelen x er mellom 8 og 12, kan vi bruke resultatene av delene A og C som følger:

P (8 ≤ x ≤ 12) = P (x ≤ 12) - P (x ≤ 8) = 0,8413 - 0,1587 = 0,6826 = 68,26.

Trening løst

Gjennomsnittsprisen på selskapets aksjer er $ 25 med et standardavvik på $ 4. Bestem sannsynligheten for at:

a) En handling har en kostnad mindre enn $ 20.

b) som har en kostnad større enn $ 30.

c) Prisen er mellom $ 20 og $ 30.

Bruk normalfordelingstabellene som er karakterisert for å finne svarene.

Løsning:

For å benytte seg av tabellene, er det nødvendig å flytte til den normaliserte eller karakteriserte variabelen:

$ 20 i den standardiserte variabelen er lik z = ($ 20 - $ 25) / $ 4 = -5/4 = -1,25 og 

$ 30 i den standardiserte variabelen er lik z = ($ 30 - $ 25) / $ 4 = +5/4 = +1.25.

a) $ 20 tilsvarer -1,25 i den standardiserte variabelen, men tabellen har ingen negative verdier, så vi plasserer +1,25 -verdien som viser verdien på 0,8944.

Hvis denne verdien trekkes fra 0,5, vil resultatet være området mellom 0 og 1,25 som forresten er identisk (med symmetri) til området mellom -1.25 og 0. Subtraksjonsresultatet er 0,8944 - 0,5 = 0,3944, som er området mellom -1.25 og 0.

Men området interesser fra -∞ til -1,25 som vil være 0,5 -0,3944 = 0,1056. Det konkluderes derfor med at sannsynligheten for at en handling er under $ 20 er 10,56%.

b) $ 30 i den karakteriserte variabelen z er 1,25. For denne verdien i tabellen vises tallet 0.8944 som tilsvarer området fra -∞ til +1.25. Området mellom +1.25 y +∞ er (1 - 0,8944) = 0,1056. Med andre ord, sannsynligheten for at en handling koster mer enn $ 30 er 10,56%.

c) Sannsynligheten for at en handling har en kostnad mellom $ 20 og $ 30 vil bli beregnet som følger:

100% -10,56% - 10,56% = 78,88%

Referanser

1. Statistikk og sannsynlighet. Normal distribusjon. Hentet fra: Projectodescartes.org
2. Geogebra. Klassisk geogebra, sannsynlighetsberegning. Gjenopprettet fra Geogebra.org
3. Mathworks. Gauss distribusjon. Gjenopprettet fra: er.Mathworks.com
4. Mendenhall, w. 1981. Statistikk for administrasjon og økonomi. 3. utgave. IBEROAMERICA REDAKSJON GROUP.
5. Stat Trek. Lær deg selv statistikk. Poisson distribusjon. Gjenopprettet fra: Stattrek.com,
6. Triola, m. 2012. Elementær statistikk. 11. Ed. Pearson Education.
7. University of Vigo. Hoved kontinuerlige distribusjoner. Gjenopprettet fra: Anapg.nettsteder.Uvigo.er
8. Wikipedia. Normal distribusjon. Gjenopprettet fra: er.Wikipedia.org