Diskrete distribusjoner
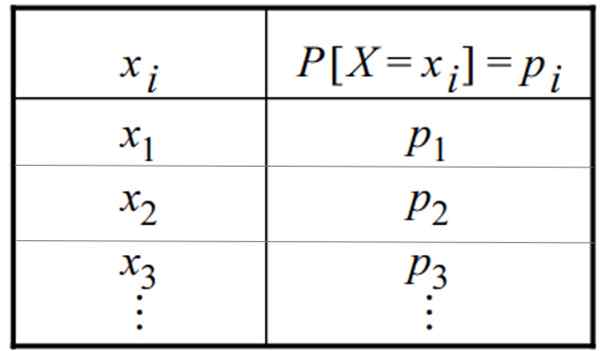
- 3940
- 189
- Magnus Sander Berntsen
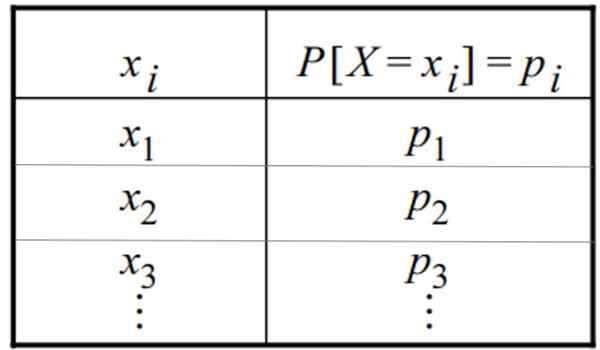 Tabell over en diskret sannsynlighetsfordeling. Kilde: f. Zapata
Tabell over en diskret sannsynlighetsfordeling. Kilde: f. Zapata Hva er en diskret distribusjon?
EN Diskret distribusjon av sannsynligheter er en funksjon f (xYo) som tildeler hver verdi av en diskret variabel: x1, x2, x3,... xYo, en viss forekomst av forekomst P (x = xYo). Denne funksjonen er også kjent som "sannsynlighetsmassefunksjon".
Den diskrete sannsynlighetsfordelingen kan gis i form av en tabell eller grafikk. En tabell har denne generelle formen, der variabelen vises i den ene kolonnen og dens respektive sannsynlighet i den andre:
Sannsynlighetsmassefunksjoner deler følgende generelle egenskaper:
- Sannsynligheten pYo av en hvilken som helst X -hendelseYo Det er mellom 0 og 1, og er til og med noen av disse grenseverdiene: 0 ≤ x ≤ 1.
- P (x = xYo) = sYo Bare ta positive verdier, derfor: P (x = xYo) ≥ 0.
- Det er sant at ∑ P (xYo) = 1 for alle mulige verdier av x.
En sannsynlighetsfordeling beskriver atferden til en populasjon, beskrevet av dens parametere: gjennomsnittet μ, variansen σ2 og standardavviket s = σ σ2.
Deretter er de mest bemerkelsesverdige diskrete distribusjonene kort beskrevet:
Uniform distribusjon
Det er den enkleste diskrete fordelingen av alle. I den kan variabelen ta "n" diskrete verdier: x1, x2, x3,... xYo, Alt med samme probabblaity. I dette tilfellet er distribusjonen gitt av:
Binomial distribusjon
Det gjelder erfaringer med bare to mulige og gjensidig utelukkende resultater, som vanligvis kalles "suksess" og "fiasko", betegnet som henholdsvis E og F. At en hendelse kalles "suksess", betyr ikke nødvendigvis at det er en god ting, det er snarere en vilkårlig betegnelse.
Sannsynligheten for suksess p (e) i “n” øving, er betegnet som p, og den for feil p (f) som q = 1 - P.
Hvis "x" representerer et visst antall suksesser i "n" uavhengige forsøk, er det sant at: 0 ≤ x ≤ n. Og sannsynligheten for forekomst P (x) av hendelsen beregnes gjennom følgende formel:
Det kan tjene deg: Square centimeter til kvadratmeter (cm² til m²)Hvor x = 0, 1, 2, 3 ..., n og symbolet (!) betyr "fabrikk":
x! = x ∙ (x - 1) ∙ (x - 2) ∙ (x - 3) ... 1
0! = 1
Poisson distribusjon
I denne distribusjonen indikerer den tilfeldige variabelen X hvor mange ganger en hendelse skjer i noen intervall, som kan være av tid, avstand eller annet. Forekomstene av hendelsen er tilfeldige, uavhengige og er fordelt jevnt gjennom det aktuelle intervallet.
Når disse forholdene, er sannsynligheten, som avhenger av gjennomsnittet av μ -forekomster og antall Euler eller antall “e”, beregnet med:
Sjansene for hendelser med denne distribusjonen er små, så det kalles "loven av sjeldne tilfeller".
Binomial distribusjonstilnærming
Poissons distribusjon fungerer som en tilnærming til binomial distribusjon når N er stor (N ≥ 100) og P er liten (NP ≤ 10). I dette tilfellet beregnes gjennomsnittlig μ som:
μ = n ∙ P
Hypergeometrisk distribusjon
Det brukes når sannsynlighetene ikke er uavhengige, det vil si etter å ha utført eksperimentet, er ikke forholdene de samme igjen. Dette er hva som skjer når du trekker ut prøver uten erstatning fra en befolkning, slik at binomialfordelingen ikke lenger kan brukes.
Hvis befolkningen består av to typer objekter som er forskjellige fra og B, og ved tilfeldige objekter og uten erstatning, er sannsynligheten for å skaffe X -objekter av type A:
Hvor A og B er de respektive mengder objekter av hver type, til stede i befolkningen.
Imidlertid, hvis befolkningen er veldig stor, selv om det ikke er noen erstatning, er det vanskelig for det samme elementet å bli valgt mer enn en gang, så begge distribusjonene: binomial og hypergeometrisk gir lignende resultater.
Kan tjene deg: Cubes Difference: Formler, ligninger, eksempler, øvelserEksempler
Mynter lanserer
Co -plartere er veldig illustrerende eksempler:
-Lanseringen av en ærlig valuta, og få et ansikt. Det er kjent at 1 ansikt har ½ sannsynlighet for å forlate og korset (0 ansikt), det samme. Distribusjonen er vist i denne tabellen:
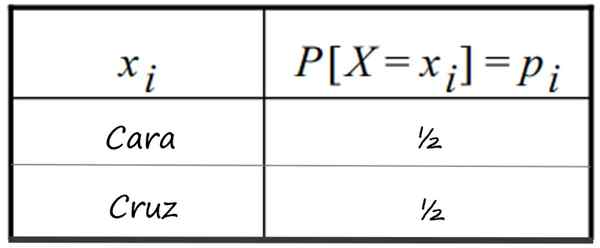 Diskret sannsynlighetsfordelingstabell som følger lanseringen av 1 ærlig valuta. Kilde: f. Zapata
Diskret sannsynlighetsfordelingstabell som følger lanseringen av 1 ærlig valuta. Kilde: f. Zapata -Samtidig skudd av to Ærlige mynter og mulige står overfor tall som kan oppnås.
 Diskret sannsynlighetsfordelingstabell som følger lanseringen av to ærlig valuta, med tanke på å få et ansikt eller ikke. Kilde: f. Zapata
Diskret sannsynlighetsfordelingstabell som følger lanseringen av to ærlig valuta, med tanke på å få et ansikt eller ikke. Kilde: f. Zapata Variabler med jevn distribusjon
-Utvalget av et heltallnummer som er jevnt eller rart: hver og en er sannsynlighet for ½ av å bli valgt i settet med hele tall.
-Lanseringen av en ærlig terning. I dette tilfellet er det 6 nummererte ansikter, og hver og en har samme sannsynlighet for å forlate: 1/6.
-Valg av et emne for å ta en eksamen, valgt mellom N -utgaver, hvis alle er like sannsynlige.
Variabler med binomial distribusjon
-Antall ansikter som kommer ut ved å lansere en ærlig mynt.
-Av en befolkning på 250 familier, antallet av disse som har 2 barn.
-Mengden palisander som overlever, etter en gartner 20 Rosales i en hage.
-Av en studie med 50 pasienter, antallet av dem som presenterte en negativ reaksjon på et medikament.
-Antall studenter som er godkjent i en sannsynlighetseksamen, av en gruppe som består av 100 studenter.
Variabler med Poisson -distribusjon
-Antall samtaler per minutt til Callcenter Av et selskap.
-Antall store jordskjelv per år for et spesifikt geografisk område.
-Antall tornadoer som påvirket en viss region i løpet av det siste året.
-Antall trær smittet med en sopp, per kvadrat hektar skog.
Variabler med hypergeometrisk distribusjon
-Suksesser av tall eller vinnende kombinasjoner i pengespill.
Kan tjene deg: Samtidig vektorer: Kjennetegn, eksempler og øvelser-Valg av et visst antall kvinner eller hanner i en prøve av n fisk av en fiskebowl.
Løste øvelser
Oppgave 1
En studie bestemte at ved tilfeldig utvalgte voksne som har smarttelefoner, bruker 54% av dem dem i klassen eller møter. Du vil finne sannsynligheten for at nøyaktig 6 av dem bruker dem i klassen eller møter å velge 8 personer med smarttelefon.
Løsning
Dette eksperimentet stemmer overens med et binomialt eksperiment, siden resultatet er binært: en person tar telefonen i klassen eller ikke tar den ut. At personen bruker telefonen som er i klassen, kan kalles suksess, og en fiasko hvis den ikke gjør det (før det ble forklart at dette valget er helt vilkårlig).
I så fall: P = 0.54 og q = 1- 0.54 = 0.46.
Siden 8 personer blir valgt tilfeldig, er n = 8 og verdien av x 6, derfor er de nødvendige verdiene tilgjengelige for å erstatte dem i binomial distribusjonsformelen:
Oppgave 2
For et siste år registrerte en klinikk 4221 fødsler. Med disse unike dataene, bestem sannsynligheten for at det er 15 fødsler på 1 dag. Er denne hendelsen sjelden?
Løsning
Poisson -distribusjon brukes, ettersom det blir bedt om å bestemme sannsynligheten for forekomst av en hendelse som oppstår i et tidsintervall. I dette tilfellet er variabelen mengden fødsler og intervallet er 1 dag.
Poisson -distribusjonsformelen trenger gjennomsnittlig fødsel per dag, som enkelt beregnes:
Derfor er sannsynligheten for x = 15 fødsler/dag:
Resultatet kan uttrykkes i form av prosent for klarhet: 6.42% sannsynlig at nøyaktig 15 fødsler på en hvilken som helst dag. Arrangementet er usannsynlig, selv om det ikke er umulig.


=\frac1n)
=\fracn!\left&space;(&space;n-x&space;\right&space;)!\cdot&space;x!\cdot\:p^x\cdot&space;q^n-x)
=\frac\mu&space;^x\cdot&space;e^-\mu&space;x!)
=\fracA!\left&space;(A-x&space;\right&space;)!\cdot&space;x!\cdot&space;\fracB!\left&space;(B-n+x&space;\right&space;)!\cdot&space;\left&space;(n-x&space;\right&space;)!\div&space;\frac\left&space;(A+B&space;\right&space;)!\left&space;(A+B-n&space;\right&space;)!\cdot&space;n!)
=\frac8!\left&space;(8-6&space;\right&space;)!\times&space;6!\times&space;0.54^6\times&space;0.46^\left&space;(8-6&space;\right&space;)=\frac8!2!\times&space;6!\times&space;0.54^6\times&space;0.46^2=0.147)

=\frac11.56^15\times&space;e^-11.5615!=0.0642)