Clausius-Clapeyron ligning Hva er det for, eksempler, øvelser
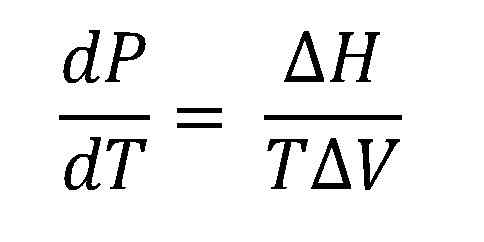
- 2971
- 185
- Prof. Theodor Gran
De Clausius-Clapeyron ligning Det er en som relaterer endringene i damptrykket og temperaturen, i en fase eller endring av tilstandsovergang. Søker om sublimeringer, fordampinger, fusjoner eller til og med i endringer i krystallinske faser. Det er verdt å nevne at denne ligningen gjelder et rent stoff som er i likevekt.
Denne ligningen stammer fra de termodynamiske lovene og P-T-diagrammer for et stoff, der sameksistenslinjen observeres; Det som skiller to forskjellige faser (væskedamp, fast-væske, etc.). For å overføre denne linjen er gevinst eller tap av varme nødvendig, for eksempel fordampningsentalpi, ΔHVap.
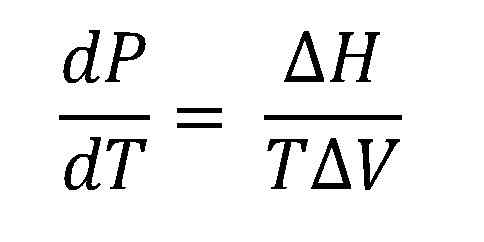 Clausius-Clapeyron ligning. Kilde: Gabriel Bolívar.
Clausius-Clapeyron ligning. Kilde: Gabriel Bolívar. Det høyere bildet viser Clausius-Clapeyron-ligningen før du blir integrert. Normalt brukes det vanligvis på væskedamper, hvor ΔH brukesVap og du vil beregne hva væskedamptrykket vil være ved en viss temperatur. Det tjener også til å beregne ΔHVap av en viss væske i et temperaturområde.
Clausisu-Clapeyron-ligning brukes også ganske ofte for å studere trykkendringer i flyktige faste stoffer; det vil si at sublimeringsentalpien vurderes, ΔHunder.
[TOC]
Hva er Clausisu-Clapeyron-ligningen for?
Beregning av trykk av trykk og fordampnings entalpier
Fra ligningen av Clausius-Clapeyron ovenfra, blir det endelig gjort noen matematiske hensyn til endelig å utføre en integrasjon. For et væskedampsystem antas det for eksempel at ΔHVap Det varierer ikke med temperaturen, og at ΔV utelukkende tilsvarer volumet på dampen, og forakter volumet på væsken (Vdamp-Vvæske = Vdamp).
Forutsatt at damp oppfører seg som en ideell gass og integrerer, oppnås ligningen for Clausius-Clapeyron integrert:
Kan tjene deg: flyktiggjøring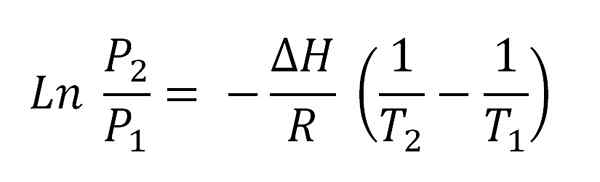 Clausius-Clapeyron ligning integrert.
Clausius-Clapeyron ligning integrert. Denne ligningen tilsvarer den for en linje som er grafisk som:
Ln p vs 1/t
Og hvis negative skråning er (ΔH/R). For å oppfylle denne ligningen, må ΔH derfor være konstant i temperaturintervallet (t2-T1) der damptrykk måles i likevekt med væsken.
På denne måten, hvis det antas at ΔH varierer lite innenfor små temperaturintervaller, er det mulig å bruke ligningen på denne linjen for å forutsi endringer i damptrykket til en væske; Og enda mer, kan du bestemme dens fordampning.
Jo større temperaturintervaller som vurderes, desto største avviket fra denne ligningen av eksperimentelle data, og jo mindre vil den bli oppfylt.
Bestemmelse av faseendringer
Dermed blir Clausius-Clapeyrs ligning utviklingen av en tangentlinje til sameksistenslinjen mellom to fysiske faser, som er observert i et hvilket som helst P-T-diagram for et stoff.
Hvis det oppstår en faseendring, vil det være en endring i skråningen, og ΔH vil ikke være den samme. Derfor, når sterke avvik er bevist og ligningen mislykkes, er det et tegn på at i temperaturintervallet opplever stoffet en annen faseendring. Det vil si at det slutter å være et væskedampersystem, siden det sendes til sameksistenslinjen som tilsvarer fast-væske- eller fastdampbalansering.
Bruk eksempler
- Clausius-Clapeyron-ligningen har blitt brukt i meteorologi for å studere atferden til skyene, selv de som er til stede på andre planeter eller måner med atmosfærer.
Kan tjene deg: glukonsyre: struktur, egenskaper, syntese, bruk- Det har blitt brukt til å bestemme fusjonsentalpien av flere metaller som natrium og gallium, og for å ekstrapolere damptrykket ved veldig høye temperaturer.
- Det har også blitt brukt for å bestemme entalpien av fordampning av stoffer som gassformig klor, karbontetraklorid, flytende vann, is og jod.
- Det har også tjent til å studere faseendringer i krystallinske strukturer. I dette siste eksemplet ser Clausius-Clapeyrs integrerte ligning bemerkelsesverdig annerledes, da de samme hensynene som tas for væskedampersystemet ikke kan gjøres for ΔV. Volumvariasjonene fra den ene fasen til den andre denne gangen er små.
Løste øvelser
- Oppgave 1
Isdamptrykket er 4.58 torr ved 0 ° C og 1.95 torr a -10 ° C. Hva er din sublimeringsentalpi i det temperaturområdet?
Merk at vi har to trykk og to temperaturer:
P1 = 4.58 Torr
P2 = 1.95 Torr
T1 = 0 ° C + 273 = 273 K
T2 = -10 ° C + 273 = 263 K
Vi konverterer temperaturenhetene fra ° C til K, fordi den konstante r av gasser har K i enhetene sine:
R = 8.314 J/K
Dermed bruker vi den integrerte Clausius-Clapeyron-ligningen og klar ΔHunder, som vil forbli som:
ΔHunder = -Rln (P2/S1) / (1 / t2 - 1 /t1)
For mer komfort vil fortsette å erstatte bare med tallene, men å vite at den endelige enheten vil være Joule:
ΔHunder = -(8.314) LN (1.95/4.58)/(1/263 - 1/273)
= 50.97 J
Eller 51.07 J Vurderer få desimaler. Denne verdien vil presentere svingninger avhengig av intervaller t2-T1 og av visse damptrykk.
- Oppgave 2
Kokepunktet for etanol ved et trykk på 760 torr (1 atm) er 78.3 ° C, og fordampningen entalpi er 39.3 kj. Hva vil være damptrykket ditt ved en temperatur på 46 ° C?
Det kan tjene deg: Tantalus: struktur, egenskaper, bruk, skaffelseVi identifiserer dataene:
P1 = 760 Torr
P2 = ?
T1 = 78.3 ° C + 273 = 351.3 k
T2 = 46 ° C + 273 = 319 K
ΔHVap = 39.3 kj eller 39300 j
Så vi må tømme P2 av den integrerte Clausius-Clapeyron-ligningen. Igjen vil enhetene bli utelatt for komfort og beregningene vil bli utviklet trinn for trinn:
LN (s2/S1) = -(ΔHVap/R) (1/t2 - 1/t1)
LN (s2/760) = -(39300/8.314) (1/319 - 1/351.3)
LN (s2/760) = -1.36
Bruke eksponentiell funksjon på begge sider av ligningen for å kunne fjerne P2 vi vil ha:
E (ln p2/760) = e(-1.36)
P2/760 = 0.256
P2 = 0.256 (760)
= 195 Torr
Ved en lavere temperatur (46 ° C), lavere damptrykk (195 Torr). Å ha etanolen et trykk på 760 torr til 78.3 ° C, vi snakker om det normale kokepunktet. Dette er atferden som forventes for alle væsker
Generelt består Clausius-Clapeyron-øvelser av denne typen av å rydde P2, T2 eller ΔH av fordampning eller sublimering. Beregningene endres betydelig når ΔV også skal vurderes, spesielt når det gjelder solid-væske-systemer eller balanser.
Referanser
- Whitten, Davis, Peck & Stanley. (2008). Kjemi. (8. utg.). Cengage Learning.
- Wikipedia. (2020). Clausius-Clapeyron-forhold. Hentet fra: i.Wikipedia.org
- San José State University. (s.F.). Clausius-Clapeyron-ligningen:
STIS -avledning og anvendelse i meteorologi. Gjenopprettet fra: SJSU.Edu - Bodner Group. (s.F.). Clausius-Clapeyron-ligningen. Hentet fra: Chemed.Chem.Purdue.Edu
- Chieh c. & Censulo a. (18. mai 2020). Clausius-Clapeyron ligning. Kjemi librettexts. Gjenopprettet fra: Chem.Librettexts.org
- Walter J. Moore. (1962). Fysisk kjemi. (Fjerde utgave). Longmans.

