I hvilke situasjoner er lineære og kvadratiske funksjoner?

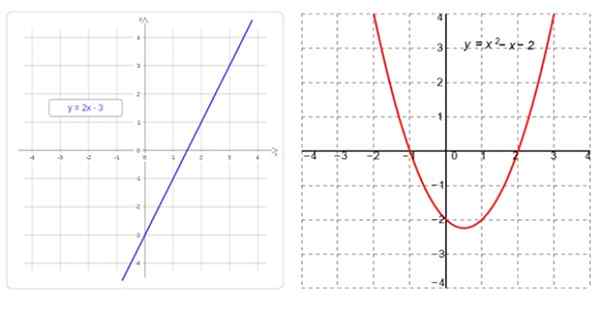
Til venstre en lineær funksjon, hvis graf er en rett linje, og til høyre, en kvadratisk funksjon, hvis graf er en parabola. Kilde: f. Zapata

Hva er lineære og kvadratiske funksjoner?

Lineære funksjoner og kvadratiske funksjoner er funksjoner som tilhører den polynomiske funksjonsgruppen. De brukes til å modellere forskjellige situasjoner, for eksempel avhengigheten mellom volumet og vekten til en kropp, mengden og kostnadene for et produkt, posisjonen kontra tid og mer.

Generelt er en funksjon et forhold som knytter to variabler og kan brukes til å modellere den virkelige verden. Polynomiske funksjoner, som navnet tilsier, kommer til uttrykk gjennom et polynom, hvis generelle form er:

f (x) = a_nxⁿ + til _N-1x ^N-1 + til_X-2x^N-2 +… til_enten

Der n er et naturlig tall, tallene til₀, til₁, til₂,… til_n De er ekte, til₀ Det er det uavhengige begrepet og til_n, Det er koeffisienten som følger med den høyeste kraften. Verdien av n indikerer typen funksjon, for n = 1 er funksjonen lineær, mens for n = 2 er funksjonen kvadratisk.

I det første av disse tilfellene reduseres det generelle uttrykket til:

f (x) = a₁x + a_enten

Og i det andre tilfellet forblir det slik:

f (x) = a₂x² + til₁x + a_enten ;   (til₂≠ 0)

Grafene over polynomfunksjonene er kontinuerlige, det vil si at de ikke opplever brå hopp eller brudd, og har dermed myk oppførsel, uten uregelmessigheter. Derfor blir de observert i modellering av mange situasjoner av vitenskap, økonomi og andre områder av menneskelig kunnskap.

Neste, interessante applikasjoner av hverandre er beskrevet mer detaljert.

Situasjoner der lineære funksjoner vises

Den lineære funksjonen er representert algebraisk av:

f (x) = a₁x + a_enten

Eller tilsvarende:

f (x) = mx + b

Dets særegne trekk er at grafen er en rett linje. Verdien m, som er koeffisienten til x, representerer ørering av denne linjen og gir et mål på hvor skrå den er.

Kan tjene deg: Ikke -lineær programmering: Metoder og øvelser

Hellingen kan være positiv, negativ eller null, men den er alltid konstant, det vil si valutakursen forblir uendret.

En skråningslinje 0 er helt horisontal, den med positiv skråning indikerer høyde eller økning (hvis en av variablene øker, den andre også, alltid med samme hastighet), og til slutt indikerer den negative skråningen reduksjon (som en av variablene øker, den andre avtar).

Verdien av b, For sin del representerer det kuttet eller skjæringspunktet mellom linjen med den vertikale aksen. Ja B = 0, Linjen går gjennom opprinnelsen til koordinatsystemet.

Modellering av eksempler med lineære funksjoner

1. Den ensartede rettlinjede bevegelsen

Ligningen som knytter X -posisjonen og tiden T for en mobil, i den ensartede rettlinjede bevegelsen, er lineær:

x (t) = v⋅t + x_enten

Hvor V, skråningen på linjen, er hastigheten på mobilen, som forblir konstant gjennom hele bevegelsen, og x_enten er startposisjonen.

2. Tetthet

Tetthet av et objekt eller et stoff, som etablerer forholdet mellom masse og volum. Ringer ρ til tettheten (den lyder "Rho"), m til deigen og V til volumet, har du:

Rydde deigen, når det gjelder volumet, oppnås det:

M = ρv

Når du tegner deigen avhengig av volumet, oppnås en rett linje hvis skråning er tettheten til objektet eller stoffet.

3. Lengde på en omkrets

Konturen til en sirkel, eller dens lengde, er proporsjonal med sin radius. Dette betyr at jo større radius, desto større er konturen omkretsen, i henhold til ligningen:

Kan tjene deg: Korrelasjonskoeffisient: Formler, beregning, tolkning, eksempel

C = 2πr

Der C er konturen eller lengden, er R radioen og π (lyder “Pi”) er en konstant hvis omtrentlige verdi er πamp3.14 ..

4. Kostnad for å sende en pakke

Siden det er lett å utlede, er den tyngre eller klumpete en dyrere pakke å transportere den. Bedrifter som er dedikert til lastetransport modellerer prisene sine etter visse regler, for eksempel:

C (x) = 2.75x

I denne ligningen er C (x) dollarkostnaden for å sende en pakke hvis vekt er x pund. Den konstante verdien 2.75 har enheter av dollar/pund (enhetskostnad).

Situasjoner der kvadratiske funksjoner vises

Algebraisk er en kvadratisk funksjon representert av:

f (x) = a₂ x² + til₁ x + a_enten

Med betingelse av at koeffisienten til₂ Være forskjellig fra 0. Den er preget av dens parabola -formede graf, hvis aksiale akse eller symmetriakse er vertikal (parallell med y -aksen)).

Krysset mellom lignelsen og nevnte akse er et punkt som kalles toppunkt. Hvis lignelsen åpnes (a₂ > 0), toppunktet er dets minimumspunkt, og hvis det åpnes ned (a₂ < 0), es el máximo.

På symmetriaksen er i fokus, et spesielt punkt som bestemmer krumningen av parabolen. Hvis sollys påvirkes på et parabolsk speil, vil strålene reflekteres på overflaten, sammenfallende i fokus, som blir oppvarmet umiddelbart.

Modellering av eksempler med kvadratiske funksjoner

1. Høyden på et prosjektil lansert vertikalt opp

Et prosjektil er ethvert objekt som en innledende hastighet er gitt og deretter frigitt, under tyngdekraftenes handling. Hvis den opprinnelige hastigheten er vertikal, størrelsesorden V₀ og rettet opp, vil objektet stige til en maksimal høyde og deretter gå ned.

Kan tjene deg: homotecia

Ligningen av høyden H som en funksjon av tiden T er:

H (t) = −4.9 t²+v₀ t

Der den vertikale sansen blir tatt som positiv, og den vertikale ned negative.

2. Banen til et horisontalt eller skrå prosjektil

Hvis en horisontal eller skrå initialhastighet er gitt til et prosjektil, vil den beskrive en parabolsk bane, som kan representeres gjennom en kvadratisk funksjon som tidligere beskrevet.

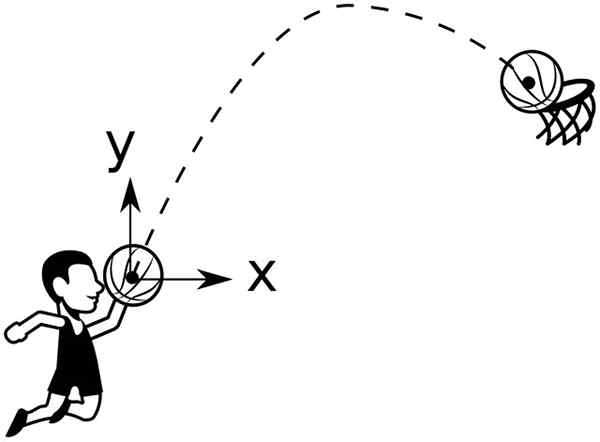Baskets ball beskriver en parabolsk bane som skal kastes i kurven. Kilde: Wikimedia Commons

For eksempel en ball kastet fra en høyde og₀, dannende vinkel θ₀ Når det gjelder horisontalt, har den en bane gitt av:

Med G som akselerasjon av tyngdekraften, som kan tilnærme 10 m/s². For eksempel et fotballkick fra bakken (og₀ = 0), med innledende hastighet på 6 m/s og vinkel på 45º med hensyn til horisontalt, vil ha en bane gitt av følgende lignelse:

3. Området til en sirkel

Jo høyere sirkelens radius, jo større er dets område være. Faktisk er sirkelområdet proporsjonalt med kvadratet av radius r, og konstanten av proporsjonalitet er tallet π:

A = πr²

4. Effektivitet av en annonse

Jo mer de ser det, jo mer effektiv en kommersiell annonse. Effektivitet E, i en skala fra 0 til 10, kan fra ett varsel modelleres i henhold til følgende kvadratiske funksjon:

Referanser 

1. Polynomiske funksjoner. Gjenopprettet etter ressurser.utdanning.er.
2. Larson, r. (2012). Forkalkning. 8. utgave. Cengage Learning.
3. Miller, c. (2013). Matematikk: resonnement og applikasjoner. 12. utgave. Pearson Education.
4. Stewart, J. (2012). Forkalkning. Matematikk for beregning. 6. utgave. Cengage Learning.
5. Zill, d. (2008). Preccculment med fremskritt av beregning. 4. plass. utgave. McGraw Hill.