Hendecagon

Hva er en endecagon?

Han Hendecagon, også kalt undecágono, Det er en flat geometrisk figur med 11 sider som tilhører Polygons -familien.

Disse er utnevnt i henhold til mengden sider de har, og i tilfelle av endecagon stammer navnet deres fra de greske ordene "Hendeka" og "Gona": henholdsvis elleve og toppunkt hjørner eller tips.

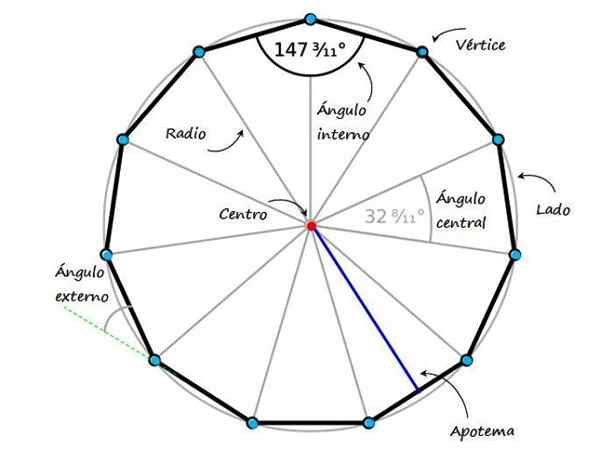
Figur 1. En vanlig endecagon og dens elementer. Kilde: f. Modifisert Wikimedia Commons -sko.

Vanlige polygoner deler en serie særegne egenskaper, spesielt. Figur 1 viser en vanlig endecagon og dens viktigste egenskaper:

• Sider, Totalt 11.
• Hjørner, Det er også 11 poeng som går sammen med to sider på rad (i forrige figur er de blå punktene, og i figur 3 er de også navngitt med store bokstaver).
• Senter, Eksidistent punkt for både toppunktene og sidene.
• Diagonaler, Linjer som går sammen med et toppunkt med et annet ikke -samlet toppunkt, totalt 44.
• Interne vinkler, De som er dannet mellom to tilstøtende sider på den indre siden av endecagon. Hvis endecagon er regelmessig, måler alle interne vinkler 147 ^3/11 º.
• Eksterne vinkler, De er dannet mellom den ene siden og forlengelsen av en av påfølgende sider.
• Radio, Avstand fra sentrum til et toppunkt.
• Sentral vinkel, at i tilfelle av vanlig endekagon måler 32 ^11/11 º, hvis sider er to tilstøtende segmenter og toppunktet i vinkelen sammenfaller med sentrum.
• Apothem, vinkelrett segment som blir med sentrum av den ene siden med midten av figuren.

Det kan tjene deg: Hipparco of Nicea: Biografi og bidrag til vitenskap

Hvordan lage en vanlig endecagon?

For å tegne en vanlig endecagon, hvis sider måler det samme, trenger du regel og kompass. En måte å lage oppsettet på er å følge disse trinnene:

1.- Tegn en omkrets og to diametre av den, en vertikal og en annen horisontal. Punktene til omkretsen bestemt av disse diametrene er navngitt og B (horisontal diameter) og C og D (vertikal diameter).

2.- Åpne kompasset med målet på sirkelradius, støtt spissen på punkt D for CD -diameteren og tegne en første bue som krysser omkretsen ved punkt E.

3.- Med samme tiltak støtter spissen av kompasset på punkt A og tegner en andre bue som krysser omkretsen på punkt F og samtidig går gjennom midten av det samme.

4.- Åpne takten med spissen støttet av E og til punkt F, og tegner en tredje bue som kutter den vertikale diameteren på punkt G.

5.- Nå, åpne kompasset mellom punktene F og G. Dette vil være målet på endecagon -siden. Spissen av kompasset støttes i F og trekker en fjerde bue som kutter til omkretsen ved punkt H, FH -siden tilhører allerede endecagon og er tegnet ved å gå sammen med poengene ved hjelp av regelen.

6.- Spissen av kompasset hviler suksessivt på punkt H og trekkes forsiktig opp, og blir sammen med punktene som bestemmes av segmenter, til de elleve sidene av polygonen.

Eksempler på Endecágonos

Det er flere typer endecargons, i henhold til målene på sidene og det i deres indre vinkler, under noen eksempler:

Vanlige og uregelmessige endeconister

-Regelmessig, Hvis alle sider og indre vinkler måler det samme.

Kan tjene deg: Euler -nummer eller nummer E: Hvor mye OK, egenskaper, applikasjoner

-Uregelmessig, Når sidene har forskjellige mål.

Følgende figur viser en vanlig endecagon i den interne konturen til en amerikansk dollar med tallet til Susan B. Anthony (1820-1906), en aktivist av kvinners rettigheter født i Massachusetts, USA. Endecagon har også blitt brukt som en del av utformingen av andre mynter over hele verden.

Figur 2. En vanlig endecagon som utgjør en del av Dollar Susan B -design. Anthony, myntet mellom 1979 og 1981, og senere lansert igjen i 1999. Kilde: Wikimedia Commons.

Konvekse og konkave Endecargons

Endecargons er forskjellige i henhold til deres indre vinkler, for eksempel kan de være:

-Konveks, Hvis de indre vinklene er mindre enn 180º.

-Konkav, Når det er indre vinkler større enn 180º.

Endecagon som dekorerer dollaren Susan B. Anthony er konveks, siden målet på noen av dens indre vinkler er mindre enn 180º. Verdien beregnes gjennom en formel som avhenger av antall sider på figuren (se følgende avsnitt).

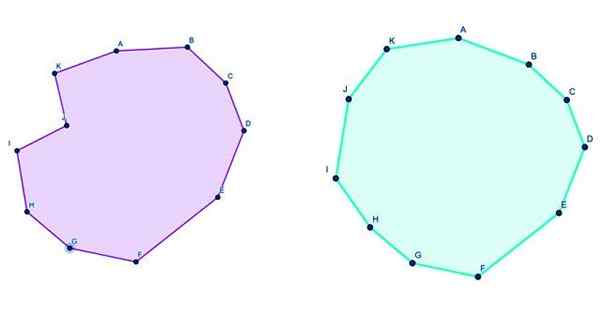Figur 3. Til venstre en konveks endecagon og til høyre en konkav endecagon. Kilde: f. Zapata gjennom Geogebra.

Formler for endecagon

Formel for indre vinkler

For å bestemme tiltaket I i grader, av de indre vinklene til en hvilken som helst vanlig polygon av n Sider, følgende formel brukes:

 Bytte ut antall sider av endecagon n = 11 i formelen oppnås:

 Og siden de indre vinklene til den vanlige endekagonen er mindre enn 180 º, er dette tallet en konveks polygon.

Summen av de interne vinklene til en vanlig polygon finnes av denne formelen, gyldig for hele og større enn 2:

Kan tjene deg: vinkler i omkretsen: typer, egenskaper, løste øvelser

S = (n - 2) x 180º

Erstatte n = 11 resultater:

S = (11 - 2) x 180º = 1620º

Eksterne vinkler

For å kjenne målet på interne vinkler, blir det brukt at summen av en intern og en ytre vinkel er lik 180º:

180 º - 147 ^3/11º = 32 ^11/11º.

Omkrets

Omkretsen er summen av sidene av endecagon, enten det er vanlig eller ikke. I tilfelle av vanlig Endekagon, hvis ℓ Det er lengden på den ene siden, omkretsen multipliserer med n, Mengden sider.

Derfor er omkretsen P for den vanlige endekagonen:

P = 11 ℓ

Område

Når du kjenner siden, kan området beregnes med formelen:

Som er omtrent:

A = 9.3656 ∙ ℓ²

En annen måte å finne området på, forutsatt at endecagon er regelmessig, er å dele det inn i basetrekanter lik siden ℓ og høyden lik lengden på apothem l l_TIL.

Området til hver trekant beregnes av:

Område = base x høyde /2

At avhengig av apothem er også skrevet som:

Område = ℓ. L_TIL /2

Og det totale arealet for endecagon multipliserer trekantområdet med 11:

A = 11ℓ. L_TIL /2

Når det gjelder omkretsen, er det vanlige endecagon -området:

A = s. L_TIL /2

Diagonaler

Antall diagonaler beregnes ved å gjøre n = 11 i følgende formel:

 D = [11 x (11-3)]/2 = 44 diagonaler.

Trening løst

Beregn omkretsen og arealet til en vanlig endecagon på 20 cm side.

Løsning

Omkretsen er:

P = 11 ℓ =11 × 20 cm = 220 cm.

Og området er:

A = 9.3656 ∙ ℓ²= 9.3656 × (20 cm)²= 3746.2 cm²

Referanser

1. Alexander, d. 2013. Geometri. 5. plass. Utgave. Cengage Learning.
2. Tegningsprofessor. Endecágono påskrevet i en omkrets (11 sider polygon). Gjenopprettet fra: YouTube.com.
3. Problemer og ligninger. Område og omkretskalkulator for den vanlige endekagonen. Hentet fra: Problemer Syuses.com.
4. Sangaku Maths. Elementer av en polygon og dens klassifisering. Gjenopprettet fra: sangakoo.com.
5. Automatisk geometri problemløsning. Endecagon. Gjenopprettet fra: Scuolaetrica.Punkt.
6. Wolfram Mathworld. Hendecagon. Gjenopprettet fra: Mathworld.Wolfram.com.