Matte

Absolutt verdi

Absolutt verdi

Hva er den absolutte verdien?

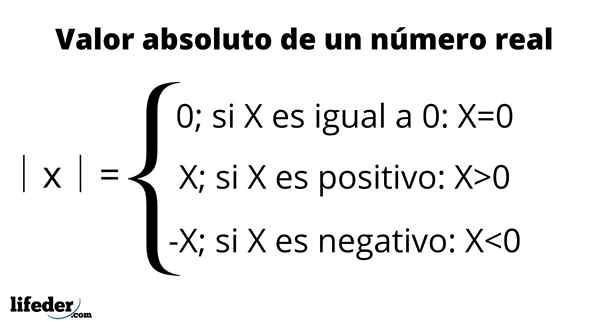
Han absolutt verdi av et reelt tall er definert som avstanden mellom det tallet og 0 av den virkelige linjen. For å være en avstand er verdien alltid positiv eller null og lik figuren til tallet.

Den absolutte verdien er representert ved å plassere tallet mellom to vertikale stenger, et symbol som leses: "Absolutt verdi av”, Som oppsummert i følgende tabell:

For eksempel er den absolutte verdien på -3 skrevet som │ -3│ og er lik 3. Dette betyr at mellom -3 og 0 er det tre enheter, som representerer tallene på den virkelige linjen. På den annen side er den absolutte verdien på +3 eller ganske enkelt 3, også lik 3, siden ved å måle avstanden til 0 er det også tre enheter.

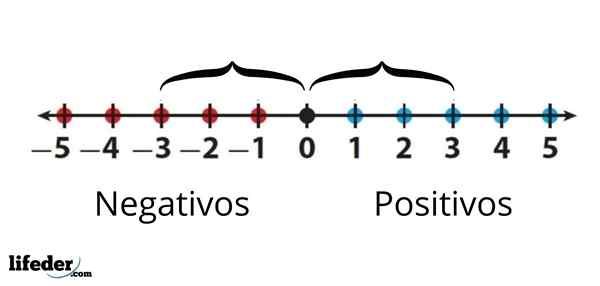Den absolutte verdien på -3 er lik den absolutte verdien på +3, siden avstanden mellom enten til 0 er den samme er den samme

Oppsummert er den absolutte verdien av et tall det samme tallet på tallet, men alltid med et positivt tegn.

Egenskaper med absolutt verdi

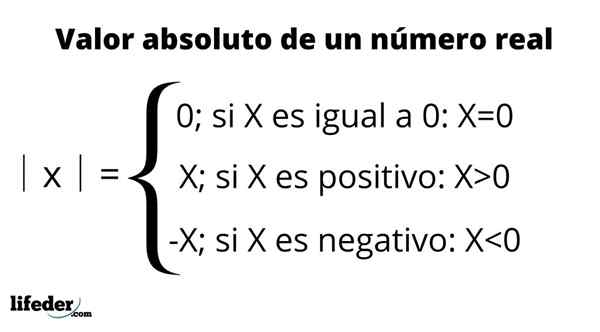Definisjon av absolutt verdi

De viktigste egenskapene til absolutt verdi:

  • 1) Den absolutte verdien av et tall er alltid positiv eller 0, derfor:

│x│≥ 0

  • 2) Den absolutte verdien på null er også null, det vil si │0│ = 0, derfor kan det bekreftes at:

│x│ = 0, ja y bare hvis x = 0

  • 3) For hvert tall x som tilhører settet med reelle tall, er den absolutte verdien av x lik den absolutte verdien av - x:

│x│ = │ - x│

  • 4) Hvis den absolutte verdien av et x -tall er a, betyr det at det er to alternativer for det tallet: i) x = +a eller ii) x = -a.
Det kan tjene deg: Mary reiser 2/4 av Cyclepisten, Melissa reiser 4/8 og Anahi reiser 3/6

For eksempel, hvis den absolutte verdien av et tall er 5, er de to mulighetene at tallet er +5 eller -5.

Operasjoner med absolutt verdi

Følgende egenskaper er veldig nyttige for å utføre operasjoner med absolutte verdier:

  • 5) For "x" og "y" som er to reelle tall, blir følgende ulikhet alltid oppfylt, kalt trekantet ulikhet av absolutt verdi:

│x│+│y│≥ │x+y│

For eksempel være:

x = -6

y = 9

Venstre side av ulikhet er:

│-6│ + │9│ = 6 + 9 = 16

Og høyre side er:

│-6+9│ = │3│ = 3

Åpenbart er 16 større enn eller lik 3, og dette er alltid tilfelle når tallene X og har forskjellige tegn. Hvis de har like tegn, oppnås likestilling. Se dette andre eksemplet med to andre forskjellige verdier:

x = -5

y = -3

│-5│+│-3│≥ │-5-3│

5+3 ≥│-8│

Faktisk:

8 = 8

  • 6) Produktet av de respektive absolutte verdiene til to reelle tall "x" og "y" er lik den absolutte verdien av produktet til tallene:

│x│ ∙ │y│ = │x ∙ y│

Igjen er verdiene:

x = -6

y = 9

Så:

│-6│ ∙ │9│ = 6 ∙ 9 = 54

Som er lik:

│ (-6) ∙ 9│ = │-54│ = 54

  • 7) Kvotienten for den absolutte verdien av to reelle tall "x" og "y", med den forskjellige nevneren på 0, er den absolutte verdien av kvotienten mellom disse tallene:

Så lenge og ≠ 0.

Eksempel:

Eksempler på absolutt verdi

Enkle eksempler

Å beregne den absolutte verdien av ethvert reelt tall er veldig enkel, for eksempel er den absolutte verdien av følgende tall:

a) │-14│ = 14

b) │-(-5) │ = │5│ = 5

c) │π│ = π

Beregninger med den absolutte verdien av et reelt tall

Utfør følgende operasjoner som involverer den absolutte verdien:

a) 2⋅│8│ + 5⋅│ -16│ -⋅│4│ = (2⋅8) + (5⋅16) - 4 = 16 + 80 - 4 = 92

b) │5- (8⋅3) │- 6 + │81 ÷ (-3) │ 

Kan tjene deg: halvparten av 15

Dette er en kombinert operasjon, så det er å foretrekke å løse den etter trinn. Den første absolutte verdien er:

│5- (8⋅3) │ = │5-24│ = │-19│ = 19

Den andre absolutte verdien som vises beregnes som følger:

│81 ÷ (-3) │ = │-27│ = 27

Deretter samles resultatene og den endelige beregningen blir utført:

│5- (8⋅3) │- 6 + │81 ÷ (-3) │ = 19- 6 + 27 = 40

Avstanden mellom to punkter på den virkelige linjen

Den absolutte verdien vises i mange applikasjoner, for eksempel å finne avstanden mellom to tall som tilhører den virkelige linjen. Hvis A er et reelt tall, er det plassert på den virkelige linjen på det punktet hvis abscissa er "A", skjer det samme med et reelt tall B.

La "A" og "B" to tall på den virkelige linjen, avstanden som skiller dem er:

dAB = │B - A│

Som også kan beregnes av:

dAB = │a - b│

For eksempel er avstanden mellom a = 5 og b = 12:

D = │5−12│ = │12−5│ = 7

På denne måten er den absolutte verdien av subtraksjonen mellom to reelle tall ganske enkelt avstanden som skiller dem på den virkelige linjen.

Absolutt verdifunksjon

Den absolutte verdifunksjonen er en applikasjon som går på settet med reelle tall ℛ til ℛ+, som tilsvarer hvert reelt tall sin absolutte verdi. Det er definert av:

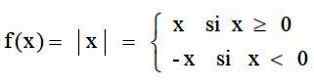
Og grafen har den typiske V -formen:

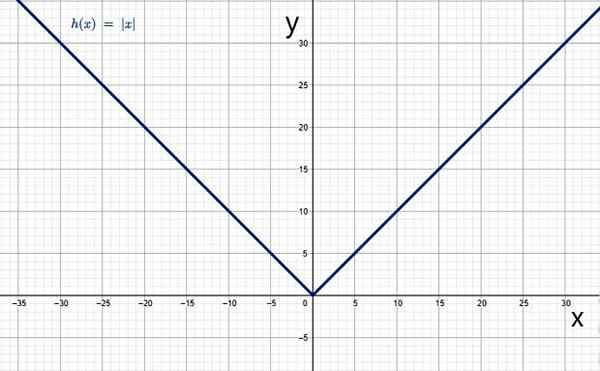Den absolutte verdien som en funksjon. Kilde: f. Zapata gjennom Geogebra.

Kjennetegn på den absolutte verdifunksjonen

-Domenet ditt er settet med alle reelle tall.

-Det er kontinuerlig.

-Det er jevnt, siden det er oppfylt at f (x) = f (-x), derfor er den vertikale aksen en symmetriakse.

-Området for den absolutte verdifunksjonen er settet med positive virkelige inkludert 0, siden funksjonen alltid representerer en avstand, og dette er alltid positivt eller null.

Kan tjene deg: Hva er retningslinjen? (Geometri)

-Det er en funksjon etter seksjoner eller av deler.

-Reduseres i intervallet (-∞, 0) og vokser inn (0,+∞).

Det absolutte verdi -argumentet kan også være en kvadratisk eller annen funksjon, for eksempel kan det defineres:

  • f (x) = │x2-5x+3│
  • g (x) = │sen x│

Den absolutte verdien er ansvarlig for å bli positiv bildene av argumentet som har et negativt tegn.

Løste øvelser

Oppgave 1

Evaluer følgende algebraiske uttrykk med absolutt verdi:

a) │2x -5│ + │ --x + 1│ ved x = 3

b) │ (x - 5) ÷ (x+4) │ ved x = −1

Løsning på

│2⋅3−5│ + │ - 3 + 1│ = │6−5│ + │ - 2│ = │1│ + 2 = 3

Løsning b

│ (−1−5) ÷ (−1+4) │ = │ (−6) ÷ (3) │ = │ - 2│ = 2

Oppgave 2

Hva er settet med verdier som representerer følgende ulikhet?

│x│≤ 3

Løsning

Ulikhet representerer alle reelle tall hvis absolutte verdi er mindre enn eller lik 3, derfor er det settet med alle tallene mellom -3 og +3, inkludert disse.

I intervallnotasjonen gjenstår det:

[-3,3]

Øvelse 3

Løs følgende ligning med absolutt verdi:

│2x-1│ = 5

Løsning 

Som tidligere antydet, for å løse en ligning med absolutt verdi, er det nødvendig å vurdere de to alternativene. Jeg mener ja:

│f (x) │ = c

Så:

1) f (x) = c

2) F (x) = -C

Derfor har denne ligningen, hvis argument er lineær, to løsninger:

Første løsning

2x - 1 = 5

2x = 6 ⇒ x1 = 3

Andre løsning

2x - 1 = -5

2x = -4 ⇒ x2 = -2

Når du evaluerer x1 = 3 eller x2 = -2 I den opprinnelige ligningen må det oppnås en likhet, på denne måten er det bekreftet at verdiene som er oppnådd er løsning av den foreslåtte ligningen. Faktisk:

│ (2⋅3) -1│ = │6-1│ = 5

Og når du prøver med det andre alternativet, oppnås også en likhet:

│2⋅ (-2) -1│ = │-4-1│ = 5

Referanser

  1. Baldor, a. 2005. Algebra. Kulturell hjemlandsgruppe.
  2. Larson, r. 2012. Forkalkning. 8. Utgave. Cengage Learning.
  3. Hoffman, J. Valg av matematikkproblemer. Volum 2.
  4. Stewart, J. 2007. Preccculment: Matematikk for beregning. 5. plass. Utgave. Cengage Learning.
  5. Zill, d. 1984. Algebra og trigonometri. McGraw Hill.