Elektromagnetisk energiformel, ligninger, bruksområder, eksempler

De Elektromagnetisk energi Det er en som sprer seg gjennom elektromagnetiske bølger (EM). Eksempel på dette er sollyset som stråler varme, strømmen som er trukket ut fra det elektriske utløpet og den som x -strålene har for å produsere røntgenbilder.

Som lydbølger når de får trommehinnen til å vibrere, er elektromagnetiske bølger i stand til å overføre energi som senere kan bli varme, elektriske strømmer eller forskjellige signaler.

Figur 1. Antenner er nødvendige i telekommunikasjon. Skiltene de jobber med har elektromagnetisk energi. Kilde: Pixabay.

Elektromagnetisk energi forplanter seg både i et material- og tomhetsmiljø, alltid i form av en tverrgående bølge og bruk av det er ikke noe nytt. Sollys er den primære kilden til elektromagnetisk energi og den eldste kjente, men å bruke strøm er noe nyere.

Det var bare i 1891 da Edison Company Sett i drift den første elektriske installasjonen i Det hvite hus i Washington DC. Og at som et supplement til gassbaserte lys som ble brukt på den tiden, fordi det til å begynne med var nok skepsis til bruk.

Sannheten er at til og med, på de mest avsidesliggende og manglende stedene, fortsetter den elektromagnetiske energien som kommer uendelig fra verdensrommet kontinuerlig å opprettholde dynamikken vi kaller hjemmet vårt i universet.

[TOC]

Formel og ligninger

Elektromagnetiske bølger er tverrbølger, der det elektriske feltet OG og magnetfeltet B De er vinkelrett på hverandre, og er også forplantningsretningen til bølgen vinkelrett på åkrene.

Alle bølger er preget av frekvensen. Det er det brede spekteret av frekvenser av EM -bølger, noe som gir dem allsidighet når de transformerer energien deres, noe som er proporsjonalt med frekvensen.

Figur 2 viser en elektromagnetisk bølge, i den elektriske feltet OG I blått svinger i flyet zy, Magnetfeltet B i rødt gjør det det i flyet Xy, Mens bølgehastigheten er rettet langs aksen +og, I henhold til koordinatsystemet som er vist.

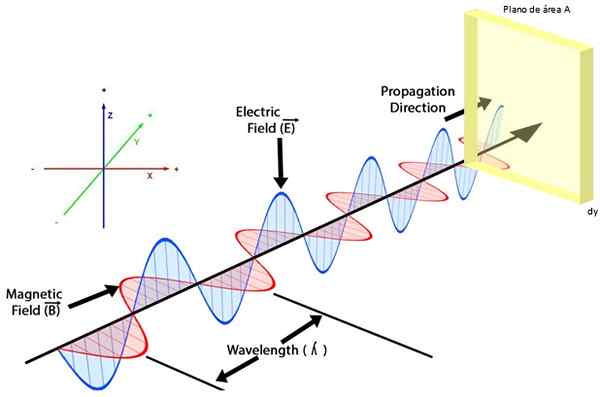Figur 2. En elektromagnetisk bølge som påvirker en overflate, leverer energi i henhold til Poynting -vektoren. Kilde: f. Zapata.

Hvis på banen til begge bølger en overflate blir brakt, la oss si et områdeplan TIL og tykkelse Dy, slik at det er vinkelrett på bølgefrekvensen, den elektromagnetiske energiflytmen per arealenhet, betegnet S, beskrives gjennom Poynting Vector:

S = (1 /μ_enten) OG × B

μ_enten Det er permeabiliteten til vakuumet (μ_enten = 4π .10^-7 Tesla. Metro/ampere), En konstant relatert til den enkle mediet gir til den elektromagnetiske bølgen for å bevege seg.

Kan tjene deg: hvit dverg

Poynting's Vector ble introdusert av den engelske astrofysikeren John Henry Poynting i 1884, en pioner i energistudien av elektriske og magnetiske felt.

Øyeblikkelig kraft per enhet

Nå må vi ta hensyn til at energi er en skalar, mens S Det er en vektor.

Husker at strømmen er energien som leveres per tidsenhet, deretter modulen til S Indikerer Øyeblikkelig kraft per enhet i retning av forplantningen av den elektromagnetiske bølgen (energioverføringshastighet).

Siden OG og B De er vinkelrett på hverandre, modulen til OG x B Det er ganske enkelt EB Og øyeblikkelig kraft (en skalar) gjenstår:

S = (1 /μ_enten) Eb

Det er lett å bekrefte at S -enhetene er watt/m² I det internasjonale systemet.

Det er fortsatt mer. Størrelsene på åkrene OG og B De er relatert til hverandre gjennom lysets hastighet c. Faktisk spredte elektromagnetiske bølger i vakuum som dette raskt. Dette forholdet er:

E = CB

Erstatte dette forholdet i S oppnås:

S = (1 /μ_enten.Ec²

Poynting -vektoren varierer med sinusformet tid, så det forrige uttrykket er den maksimale verdien, fordi energien som leveres av den elektromagnetiske bølgen også svinger, akkurat som feltene gjør. Selvfølgelig er frekvensen av svingning veldig stor, så det er ikke mulig å oppdage det i synlig lys, for eksempel.

applikasjoner

Blant de flere bruksområdene som vi allerede har sagt, har elektromagnetisk energi, her er to som kontinuerlig brukes i mange applikasjoner:

Dipolo -antenne

Antennene er overalt som fyller plassen med elektromagnetiske bølger. Det er sendere, som for eksempel transformerer elektriske signaler til radio- eller mikrobølgeovnbølger. Og det er reseptorer, som gjør omvendt arbeid: de samler bølgene og gjør dem til elektriske signaler.

La oss se hvordan du lager et elektromagnetisk signal som sprer seg i verdensrommet, fra en elektrisk dipol. Dipolen består av to elektriske ladninger av like stor størrelse og motsatte tegn, atskilt med en liten avstand.

Kan tjene deg: elektriske ledere

I den følgende figuren er det elektriske feltet OG Når belastningen + er oppe (venstre figur). OG peker ned på det viste punktet.

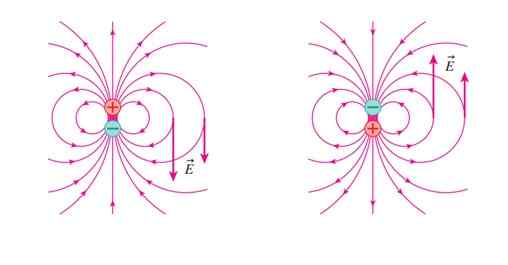Figur 3. Elektrisk felt av en dipol i to forskjellige posisjoner. Kilde: Randall Knight. Fysikk for forskere og ingeniører.

I figur 3 til høyre endret dipolen posisjon og nå OG peker opp. Vi gjentar denne endringen mange ganger og veldig raskt, la oss si frekvens F. Et felt opprettes slik OG Variabel i tid gir opphav til et magnetfelt B, også variabel og hvis form er sinus (se figur 4 og under eksempel 1).

Og hvor Faradays lov sikrer at et magnetfelt B Variabel i tid gir opphav til et elektrisk felt, fordi det viser seg at det å gjøre dipolen allerede har et elektromagnetisk felt som er i stand til å spre seg.

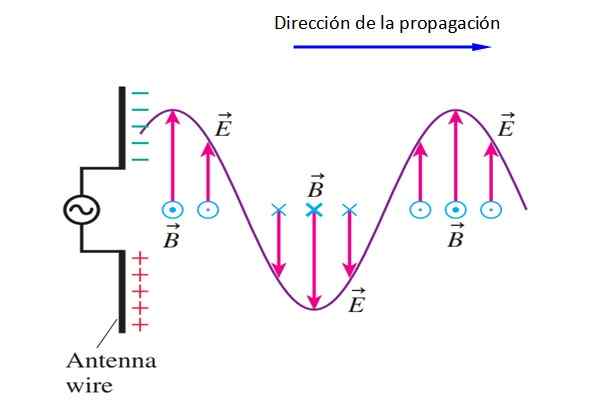Figur 4. En dipolantenne genererer et signal som transporterer elektromagnetisk energi. Kilde: f. Zapata.

Jeg føler det B peker inn eller ut av skjermen vekselvis (den er alltid vinkelrett på OG).

Elektrisk feltenergi: kondensatoren

Kondensatorene har dyden med å lagre elektrisk ladning og derfor elektrisk effekt. De er en del av mange enheter: motorer, radio- og TV -kretsløp, billyssystem og mye mer.

Kondensatorene består av to separate drivere en liten avstand. Hver og en er tildelt en masse samme størrelsesorden og det motsatte tegnet, for deretter å lage et elektrisk felt i rommet mellom de to sjåførene. Geometrien kan variere, og være en kjent den av den flat-parallelle plakkkondensatoren.

Energien som er lagret i en kondensator kommer fra arbeidet som ble gjort for å laste den, som tjente til å lage det elektriske feltet inne. Vi introduserer et dielektrisk materiale mellom platene, kondensatorens kapasitet øker og derfor energien som dette kan lagre.

En kapasitetskondensator og opprinnelig tømmes ut, som lastes av et batteri som leverer en V -spenning, til den når en Q -belastning, lagrer en energi eller gitt av:

U = ½ (q²/C) = ½ qv = ½ cv²

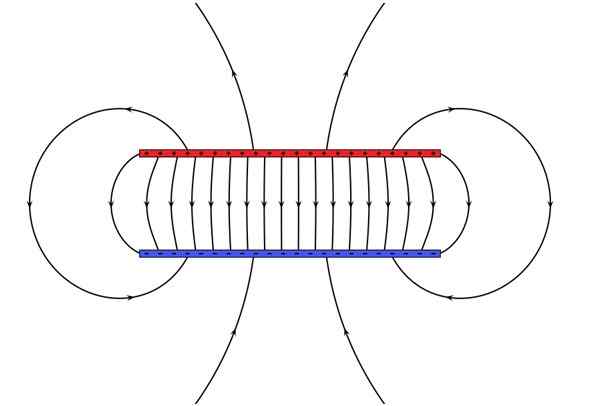Figur 5. En parallell flatplater kondensator lagrer elektromagnetisk energi. Kilde: Wikimedia Commons. Geek3 [CC BY-SA 4.0 (https: // creativecommons.Org/lisenser/by-SA/4.0)].

Eksempler

Eksempel 1: Intensiteten til en elektromagnetisk bølge

Tidligere ble det sagt at størrelsen på den poyntingvektoren tilsvarer kraften som bølgen leverer for hver kvadratmeter overflate, og at i tillegg er den tidsavhengige vektoren, dens verdi svingte opp til maksimalt maksimalt maksimalt S = s = (1 /μ_enten.Ec².

Gjennomsnittsverdien på S i en bølgesyklus er lett å måle og indikerer bølgeenergien. Denne verdien er kjent som bølgeintensitet Og det beregnes på denne måten:

Kan tjene deg: Hva er dynamisk balanse? (Med eksempel)

I = s_halv = S = (1 /μ_enten.Ec²_halv

En elektromagnetisk bølge er representert med en sinusfunksjon:

E = e_enten Sen (kx - ωt)

Hvor OG_enten Det er bølgenes amplitude, k Bølgenummeret og Ω Vinkelfrekvensen. Så:

Gjennomsnittsverdien av SEN -funksjonen² x i en syklus er ½. Det er formelt beregnet av følgende uttrykk, som er mulig å verifisere ved hjelp av en integrert tabell eller utføre det integrerte analytisk:

Derfor s_halv Det forblir som:Når en kilde avgir likt i alle retninger, blir kraften utstrålet i henhold til det inverse til kvadratet av avstanden til kilden (figur 5). Ja P_m Det er den gjennomsnittlige kraften, da, på avstand r Intensiteten Yo av signalet er det gitt av:

Figur 5. Antennen stråler signalet i sfærisk form. Kilde: f. Zapata.

Eksempel 2: Søknad på en overføring av antenne

Det er en radiostasjon som overfører et 10 kW -signal om kraft og frekvens på 100 MHz, som sprer seg i en sfærisk form, som i figuren over.

Finn: a) Amplituden til de elektriske og magnetiske felt på et punkt som ligger 1 km fra antennen og b) den totale elektromagnetiske energien som påvirker et firkantet ark 10 cm i en periode på 5 minutter.

Dataene er:

Lyshastighet i vakuum: C = 300.000 km/s

Vakuumpermeabilitet: μ_enten = 4π .10^-7 T.M/A (Tesla. Metro/ampere)

Løsning på

Ligningen gitt i eksempel 1 brukes til å finne intensiteten til den elektromagnetiske bølgen, men først må verdiene i det internasjonale systemet uttrykkes:

10 kW = 10000 W

100 MHz = 100 x 10⁶ Hz

Ir disse verdiene erstattes i ligningen for intensitet, siden det er en kilde som avgir likt (kilde isotropisk):

Dette er nettopp gjennomsnittlig effekt per enhet med gjennomsnittlig område eller verdi av Poynting Vector Module:

Tidligere ble det sagt at størrelsen på OG og B De var relatert til lysets hastighet:

E = CB

B = (0.775/300.000.000) t = 2.58 x 10^-9 T

Løsning b

S_halv Det er strøm per enhet og på sin side er strømmen energi per tidsenhet. Multipliserer s_halv For plateområdet og for eksponeringstiden oppnås det forespurte resultatet:

5 minutter = 300 sekunder

Område = (10/100)²  m² = 0.01 m².

U = 0.775 x 300 x 0.01 Joules = 2.325 Joules.

Referanser

1. Figueroa, d. (2005). Serier: Fysikk for vitenskap og ingeniørfag. Volum 6. Elektromagnetisme. Redigert av Douglas Figueroa (USB). 307-314.
2. ICES (International Committee on Electromagnetic Safety). Elektromagnetiske energifakta, og et kvalitativt syn. Gjenopprettet fra: Ices-EmfSafety.org.
3. Knight, r. 2017. Fysikk for forskere og ingeniørfag: En strategitilnærming. Pearson. 893 - 896.
4. Portland State University. Em Waves Trate Energy. Gjenopprettet fra: PDX.Edu
5. Hva er elektromagnetisk energi og hvorfor er det viktig?. Gjenopprettet fra: Sciencestruck.com.