Gibbs gratis energienheter, hvordan det beregnes, løste øvelser

De Gibbs gratis energi (Vanligvis kalt G) er et termodynamisk potensial definert som forskjellen i entalpi H, bortsett fra produktet av temperaturen T, av systemets entropi:

G = h - t s

Gibbs gratis energi måles i Joules (ifølge det internasjonale systemet), i Ergios (for ligasystemet for enheter), i kalorier eller elektron volt (For elektro volt).

Figur 1. Diagram som viser definisjonen av Gibbs Energy og dets forhold til de andre termodynamiske potensialene. Kilde: atomkraft.nett.

I prosessene som oppstår ved konstant trykk og temperatur, er variasjonen av Gibbs fri energi ΔG = ΔH - T ΔS. I slike prosesser representerer (g) energien som er tilgjengelig i systemet som kan bli arbeid.

For eksempel, i eksotermiske kjemiske reaksjoner, synker entalpien mens entropi øker. I Gibbs -funksjonen blir disse to faktorene motvirket, men bare når Gibbs -energien reduserer reaksjonen oppstår spontant.

Så hvis variasjonen av G er negativ, er prosessen spontan. Når Gibbs -funksjonen når sitt minimum, når systemet en stabil likevekt. Kort sagt, i en prosess som trykk og temperatur forblir konstant kan vi bekrefte:

- Hvis prosessen er spontan, så ΔG < 0

- Når systemet er i balanse: Δg = 0

- I en ikke-spontan prosess øker den: Δg> 0.

[TOC]

Hvordan beregnes det?

Gibbs Free Energy (G) beregnes av definisjonen gitt i begynnelsen:

G = h - t⋅s

På sin side er entalpi H et termodynamisk potensial definert som:

H = u + p v

- Steg for steg

Deretter vil en trinn -by -trinn -analyse bli gjort, for å kjenne de uavhengige variablene som Gibbs Energy er en funksjon:

1- Av den første loven om termodynamikk er intern energi relatert til systemets entropi og dets volum V for reversible prosesser gjennom differensialforholdet:

Det kan tjene deg: etidiumbromid: struktur, egenskaper, bruksområder, toksisitet

du = dq - dw = tds - pdv

Fra denne ligningen følger det at intern energi u er en funksjon av variablene S og V:

U = u (s, v)

2- Starter fra definisjonen av H og å ta differensialet oppnås:

dh = du + d (p v) = du + vdp + pdv

3- Å erstatte uttrykket for du oppnådd i (1) du må:

DH = TDS - PDV + VDP + PDV = TDS + VDP

Herfra er det konkludert med at entalpi H avhenger av entropi s og trykk p, det vil si:

H = h (s, p)

4- Nå beregnes den totale Gibbs Free Energy Differensialet å oppnå:

DG = DH -TDS ​​-SDT = TDS + VDP -TDS ​​-SDT

Hvor DH er erstattet av uttrykket som finnes i (3).

5- Til slutt, ved å forenkle du får: DG = VDP - SDT, Det er tydelig at fri energi G avhenger av trykket og temperaturen t som:

G = g (p, t)

- Maxwells termodynamiske forhold

Fra analysen i forrige seksjon følger det at den interne energien til et system er en funksjon av entropi og volum:

U = u (s, v)

Da differensialet av ELLER være:

du = ∂_SU |_V Ds + ∂_VU |_S DV = TDS - PDV

Fra dette uttrykket i delvis derivater kan de så -kallede maxwell termodynamiske forholdene trekkes ut. Delvis derivater gjelder når en funksjon avhenger av mer enn en variabel og enkelt beregnes ved å anvende teoremet til følgende avsnitt.

Maxwells første forhold

 ∂_VT |_S = -Mon_SP |_V 

For å komme til dette forholdet, Clairaut teorem - Schwarz På delvis derivater, som sier følgende:

"Den andre orden blandede derivater med de utvekslede variablene er de samme, forutsatt at funksjonene som skal avledes er kontinuerlige og differensierbare".

Maxwells andre forhold

Starter fra det som ble demonstrert i punkt 3 i forrige seksjon:

Kan tjene deg: faktorer som påvirker løseligheten

H = h (s, p) og dh = tds + vdp

Kan fås:

 ∂_PT |_S = ∂_SV |_P 

Fortsett på en lignende måte med Gibbs gratis energi G = g (p, t) Og med den frie energien til Helmholtz F = f (t, v) For å få de to andre termodynamiske forholdene til Maxwell. 

Figur 2. Josiah Gibbs (1839-1903) var en amerikansk fysiker, kjemiker og matematiker som ga store bidrag til termodynamikk. Kilde: Wikimedia Commons.

Maxwells fire termodynamiske forhold 

1- assosiert med intern energi u: ∂_VT |_S = -Mon_SP |_V

2- Den som er oppnådd fra entalpi H: ∂_PT |_S = ∂_SV |_P 

3- relatert til energien til Helmholtz f: ∂_TP |_V = ∂_VS |_T 

4- Koblet til den frie energien til Gibbs G: ∂_TV |_P = -Mon_PS |_T

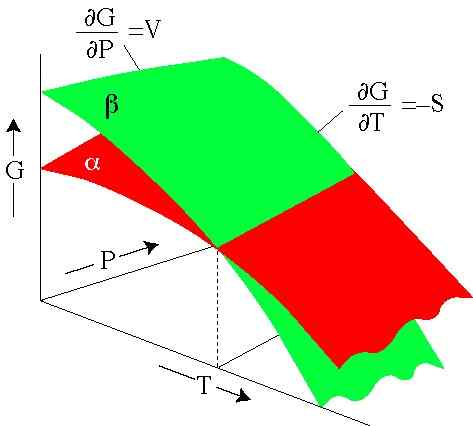Figur 2. Gibbs 'energi avhenger av trykk og temperatur. Hver overflate representerer en fase. (Serc.Carleton.Edu)

Løste øvelser

Oppgave 1

Beregn variasjonen av Gibbs fri energi for 2 mol ideell gass ved en temperatur på 300K under en isotermisk ekspansjon som fører til det opprinnelige volumsystemet på 20 liter til et sluttvolum på 40 liter.

Løsning

Å huske definisjonen av Gibbs gratis energi er:

G = h - t s

Da vil en endelig variant av F være:

ΔG = ΔH - T ΔS, Siden Δt = 0

I ideelle gasser avhenger entalpi bare av dens absolutte temperatur, men ettersom det er en isotermisk prosess, så ΔH = 0 og ΔG = - T ΔS.

For ideelle gasser er entropivariasjonen av en isotermisk prosess: 

ΔS = nr ln (v₂/V₁)

Det gjaldt saken om denne øvelsen vi har:

ΔS = 2 Mol X 8,314 J/(K mol) x Ln (40L/20L) = 11,53 J/K

Da kan vi få endringen i Helmholtzs energi:

Δg = - 300k x 11,53 j/k = -3457,70 j.

Oppgave 2

Tatt i betraktning at Gibbs fri energi er en funksjon av temperatur og trykk G = G (T, P); Bestem variasjonen av G under en prosess der temperaturen ikke endres (isotermisk) for N mol av en ideell monoatomisk gass.

Kan tjene deg: Strontium hydroxide (SR (OH) ₂)

Løsning

Som demonstrert ovenfor, avhenger endringen i Gibbs 'energi bare av endringen i temperatur T og volum V, så en uendelig variasjon av den beregnes i henhold til:

DG = -SDT + VDP

Men hvis det er en prosess der temperaturen er konstant, er DF = + VDP, så en begrenset variasjon av trykk ΔP fører til en endring i Gibbs -energien gitt av:

Δg = + ∫ vdp = + ∫ (n r t) dp/p = + n r t ln (Δp)

Bruke den ideelle gassligningen:

P v = n r t

Under en isotermisk prosess hender det at:

D (p v) = p dv + v dp = 0

Det er:

dp/p = - dv/v

Så det forrige resultatet kan skrives avhengig av volumvariasjonen ΔV:

Δg = + ∫ vdp = + ∫ (n r t) dp/p = - ∫ (n r t) dv/v = -n r t ln (ΔV)

Øvelse 3

Tatt i betraktning følgende kjemiske reaksjon:

N₂0 (g) + (3/2) eller₂ (g) ↔no₂ (g) Ved temperatur t = 298 k

Finn variasjonen av Gibbs fri energi og gjennom det oppnådde resultatet, angi om det er en spontan prosess eller ikke.

Løsning

Under trinnene:

- Første trinn: Reaksjonsentalpier

Δhr = 2*Δh (nei₂ (g)) - Δh (n₂0 (g)) = 2*33.2-81.6 = -15.2KJ/mol

- Andre trinn: Reaksjonsentropi -variasjonen

ΔSr = 2*s (nei₂ (g)) - S (n₂0 (g)) - (3/2) s (eller₂ (g)) = 2*240,1 - 220,1 - 1,5*205,2 = -47,7 j/(mol*k).

- Tredje trinn: Variasjon i Gibbs -funksjonen

Denne verdien vil avgjøre balansen mellom synkende energi og øke entropien for å vite om reaksjonen endelig er spontan eller ikke.

ΔGr = ΔHR -t ΔSR = -15,2 -298*(-47,7) = -985,4 J/mol

Siden det er en negativ variant av Gibbs -energi, kan det konkluderes med at det er en spontan reaksjon ved temperaturen på 298 K = 25 ºC.

Referanser

1. Castaños e. Gratis energiøvelser. Gjenopprettet fra: lidiaconlachimica.WordPress.com.
2. Cengel, og. 2012. Termodynamikk. 7. utgave. McGraw Hill.
3. Librettexts. Gibbs gratis energi. Gjenopprettet fra: Chem.Librettexts.org
4. Librettexts. Hva er gratis energi. Gjenopprettet fra: Chem.Librettexts.org
5. Wikipedia. Gibbs gratis energi. Gjenopprettet fra: er.Wikipedia.com
6. Wikipedia. Gibbs gratis energi. Hentet fra: i.Wikipedia.com