Helmholtz gratis energienheter, hvordan det beregnes, løste øvelser

De Helmholtz gratis energi Det er et termodynamisk potensial som måler nyttig arbeid med et lukket system i konstant temperatur og volumforhold. Helmholtzs frie energi er betegnet som F Og det er definert som forskjellen fra indre energi ELLER Mindre temperaturproduktet T For entropi S:

F = u - t⋅s

Siden det er energi, måles det i joules i det internasjonale systemet (SI), selv om andre passende enheter også kan være ergios (CGS), kalorier eller elektron volt (EV).

Figur 1. Definisjon av Helmholtzs energi. Kilde: Pixabay.

Den negative variasjonen av Helmholtzs energi under en prosess blir likestilt med det maksimale arbeidet som systemet kan utføre i en isokorisk prosess, det vil si til konstant volum. Når volumet ikke er konstant, kan en del av dette arbeidet gjøres på miljøet.

I dette tilfellet refererer vi til arbeid der volumet ikke varierer, for eksempel elektrisk arbeid: DW = φDQ, med φ som det elektriske potensialet og Q som elektrisk ladning.

Hvis temperaturen også er konstant, minimeres Helmholtzs energi når balansen er nådd. For alt dette er Helmholtzs energi spesielt nyttig i konstante volumprosesser. I dette tilfellet har du:

- For en spontan prosess: Δf < 0

- Når systemet er i likevekt: Δf = 0

- I en ikke-spontan prosess: Δf> 0.

[TOC]

Hvordan beregnes Helmholtz fri energi?

Som nevnt i begynnelsen, er Helmholtzs energi definert som "den interne energien eller systemet, bortsett fra produktet av systemet absolutte T -temperatur, av systemets entropi":

F = u - t⋅s

Det er en funksjon av temperaturen T og volum V. Trinnene for å visualisere dette er følgende:

Kan tjene deg: interne elektroner

- Med utgangspunkt i den første loven om termodynamikk, intern energi eller er relatert til systemets entropi og dets volum V for reversible prosesser gjennom følgende differensialforhold:

du = dq - dw = tds - pdv

Dette følger at intern energi eller er en funksjon av variabler S og V, derfor:

U = u (s, v)

- Nå definisjonen av F Og den er avledet:

df = du - d (ts) = du - tds - sdt

- Erstatning der differensialuttrykket oppnådd for DU i det første trinnet, gjenstår:

DF = TDS - PDV - TDS - SDT = -SDT - PDV

- Til slutt konkluderes det med at F er en funksjon av temperaturen T og volum V og kan uttrykkes som:

F = f (t, v)

Figur 2. Hermann von Helmholtz (1821-1894), tysk fysiker og lege, anerkjent for sine bidrag til elektromagnetisme og termodynamikk, blant andre vitenskapsområder. Kilde: Wikimedia Commons.

Spontane prosesser

Helmholtzs energi kan brukes som et generelt kriterium for spontanitet i isolerte systemer, men før noen konsepter skal spesifiseres:

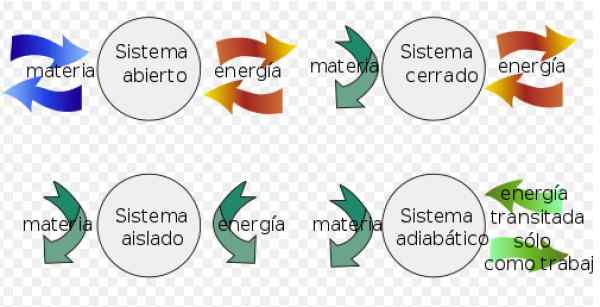
- EN Systemet lukket Den kan utveksle energi med miljøet, men kan ikke utveksle noe.

- I stedet a isolert system utveksler ikke materie eller energi med miljøet.

- Endelig en åpent system utveksling og energi med miljøet. 

Figur 3. Termodynamiske systemer. Kilde: Wikimedia Commons. Fjgar (bis) [CC By-SA (https: // CreativeCommons.Org/lisenser/by-SA/4.0)].

I reversible prosesser beregnes variasjonen i indre energi som følger:

Du = tds - pdv

Anta nå en konstant volum (isokorisk) prosess, der den andre termin av forrige uttrykk har et nullbidrag. Det må også huskes at i henhold til Clausius ulikhet: 

ds ≥ dq/t

Slik ulikhet gjelder et isolert termodynamisk system.

Slik at for en prosess (reversibel eller ikke) der volumet opprettholdes konstant er oppfylt:

Kan tjene deg: fosforsyre (H3PO4)

T ds ≥ du (Ved fast volum)

Tatt i betraktning det:

df = du - t ds 

Vi må i en isokorisk prosess ved konstant temperatur oppfylt at: Df ≤ 0, Som antydet i begynnelsen.

Slik at Helmholtz Fs energi er en synkende mengde i en spontan prosess mens det er et isolert system. F når sin minste og stabile verdi når reversibel balanse er nådd.

Løste øvelser

Oppgave 1

Beregn variasjonen av den frie energien til Helmholtz F for 2 mol ideell gass ved en temperatur på 300K under en isotermisk ekspansjon som fører til systemet med et innledende volum på 20 liter til et sluttvolum på 40 liter.

Løsning

Starter fra definisjonen av f:

F = u - t s

Da vil en endelig variant av F, kalt ΔF, være:

Δf = ΔU - T ΔS

Som uttalelsen sier at temperaturen er konstant: Δt = 0. Imidlertid avhenger indre energi i ideelle gasser bare av dens absolutte temperatur, men siden det er en isotermisk prosess, så ΔU = 0 og Δf = - T ΔS. For ideelle gasser skrives entropivariasjonen av en isotermisk prosess som denne: 

ΔS = n.R.LN (v₂/V₁)

Bruke dette uttrykket:

ΔS = 2 Mol X 8,314 J/(K mol) x Ln (40L/20L) = 11,53 J/K

Endelig er endringen i Helmholtzs energi:

ΔF = - T ΔS = - 300K x 11,53 J/K = -3457,70 J.

Oppgave 2

Inne i en sylinder er det et stempel som deler det inn i to seksjoner og på hver side av stempelet er det n Mol av en ideell monoatomisk gass, som vist på figuren nedenfor.

Sylinderveggene er gode varmeledere (diatermisk) og er i kontakt med et T -temperaturreservoar_enten.

Det første volumet til hver av sylinderseksjonene er v_1I og v_2i, Mens de endelige volumene er v_1f og v_2f Etter en kvasiestatisk forskyvning. Stempelet beveger seg ved hjelp av en stempel som hermetisk krysser de to sylinderen tapas.

Det kan tjene deg: Tecnecio (TC): Struktur, egenskaper, bruksområder, innhenting

Det blir bedt om å finne:

a) Endringen i den indre energien av gass og arbeidet som er utført av systemet og

b) Helmholtzs energikariasjon.

Løsning på

Når stempelet beveger seg kvasiestatisk, må den ytre kraften som påføres stempelet balansere kraften på grunn av trykkforskjellen i de to delene av sylinderen.

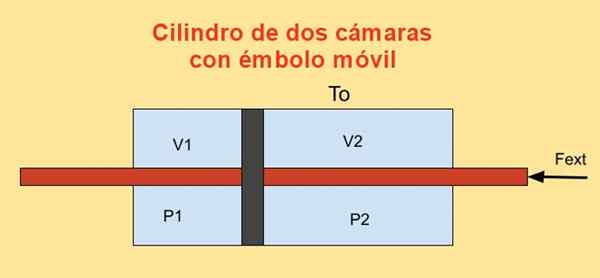Figur 4. Variasjon av fri energi F i en sylinder med to kameraer. Kilde: f. Zapata.

Jobben Dw Laget av ekstern kraft F_ext Under en uendelig forskyvning Dx er:

Dw = - f_ext Dx = (P₁ - P₂) En dx = p₁ Dv₁ + P₂ Dv₂

Der forholdet har blitt brukt Dv₁ = - DV₂ = En dx, å være til Stempelområdet. På den annen side er variasjonen av Helmholtzs energi: 

Df = -Sdt - PDV

Siden i løpet av prosessen ikke endres, da dt = 0 og DF = - PDV. Bruke dette uttrykket på hver seksjon av sylinderen du har:

DW = s₁ Dv₁ + P₂ Dv₂ = - df₁ - Df₂

Å være F₁  og F₂ Helmholtzs energier i hvert av kameraene.

Endelig W -arbeid kan beregnes ut fra den endelige variasjonen av Helmholtzs energi på hvert kamera:

W = -Δf₁ - Δf₂

Løsning b

For å finne endring av energi fra Helmholtz, brukes definisjonen: F = u - t s. Som i hvert kamera har du en ideell monoatomisk gass ved konstant temperatur T_enten, Intern energi endres ikke (ΔU = 0), slik at: Δf = - t_enten ΔS. I tillegg:

ΔS = nr ln (v_F/Sag)

At ved å erstatte det endelig tillater arbeidet som er gjort, er: 

W = -t_enten Nr ln (v_1f /V_1I) -To nr ln (v_2f /V_2i) = -Δf₁ -Δf₂

W = - til nr ln [(v_1f ⋅ V_1I)/(V_{2f .}V_2i)] = - Δf_Total

Å være Δf_Total Den totale variasjonen av Helmholtzs energi.

Referanser

1. Castaños e. Gratis energiøvelser. Gjenopprettet fra: lidiaconlachimica.WordPress.com
2. Librettexts. Helmholtz Energy. Gjenopprettet fra: Chem.Librettexts.org
3. Librettexts. Hva er gratis energi. Gjenopprettet fra: Chem.Librettexts.org
4. Wikipedia. Helmholtz Energy. Gjenopprettet fra: er.Wikipedia.com
5. Wikipedia. Helmholtz gratis energi. Hentet fra: i.Wikipedia.com