Oversettelsesbalanseforhold, eksempler, øvelser

Det anføres at et objekt er i Oversettelsesbalanse Når summen av styrkene som virker på ham er null. Dette betyr ikke at det nødvendigvis er resten, men bevegelsen, hvis eksisterende, ville være ensartet eller utelukkende rotasjon.

Mekaniske likevektsforhold er basert på Newtons lover om mekanikk. Faktisk forteller den første loven at et objekt er i ro eller beveger seg med ensartet rettlinjet bevegelse MRU, forutsatt at ingen nettokraft virker på den.

Denne lamposten er i oversettelsesbalanse

Nå er den resulterende nettokraften eller kraften ganske enkelt vektorsummen til alle kreftene som virker på objektet. I henhold til Newtons andre lov, må denne summen være lik produktet mellom masse og akselerasjon, men hvis objektet ikke er akselerert, er denne summen annullert.

Og ettersom det ikke er noen akselerasjon er de to mulighetene som er nevnt: kroppen er i ro, det vil si at den ikke beveger seg, eller hvis den gjør det, må den være med MRU. I det første tilfellet er det snakk om statisk transnasjonal balanse, og i den andre dynamiske.

Oversettelsesbalansen er en viktig faktor i mange aspekter ved prosjektering, for eksempel i konstruksjonen. Elementene som utgjør en bygning: bjelker, kabler, rammer og mer, må være i balanse for å garantere stabiliteten til kabinettet.

Oversettelsesbalansen søkes også i mobile strukturer, for eksempel mekaniske trapper, transportbånd og i utøvelse av en rekke idretter.

[TOC]

Oversettelsesbalansetilstand

Anta at flere krefter virker på et organ, som vi betegner som F₁, F₂, F₃.. . F_n, Bruke fet bokstav for å fremheve det faktum at krefter er vektorer og må legges til som sådan.

Vektorsummen til alle disse kreftene kalles resulterende kraft enten Nettokraft. Hvis denne summeringen resulterer i nullvektoren, er betingelsen for oversettelsesbalansen oppfylt:

Kan tjene deg: lukket elektrisk krets

F₁+ F₂+ F₃.. .+ F_n = 0

Denne tilstanden kan skrives kompakt ved hjelp av summering:

∑ F_Yo = 0

Når det gjelder komponentene i den resulterende kraften, kan den forrige ligningen, som er vektor, deles inn i tre skalarligninger, en for hver komponent i den resulterende kraften:

∑ f_Ix = 0; ∑ f_og = 0 og ∑ f_z = 0

I praksis er det ikke lett.

Dette er grunnen til at virkelige gjenstander nesten aldri er fritatt for eksterne krefter, og som en konsekvens er det vanskelig å oppnå balansen i oversettelsen.

Så ingeniører bruker mekanismer for å redusere gnidning, for eksempel lagre og bruk av smøremiddeloljer.

Gratis kroppsdiagrammer

Det frie kroppsdiagrammet er et skjema der kreftene som virker på kroppen trekkes. Når balansen mellom oversettelse er søkt, må disse styrkene balanseres. For eksempel, hvis du oppfører en vertikal kraft rettet ned, for eksempel vekt, må det være en vertikal kraft opp som har nøyaktig samme størrelse.

Denne kraften kan leveres av hånden som tåler gjenstanden slik at den ikke faller, et tau eller bare overflaten på et bord.

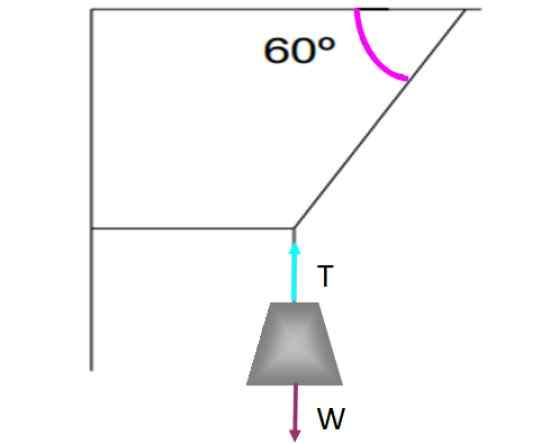
Hvis det er en tangensiell kraft på overflaten, for eksempel kinetisk eller statisk friksjon, må det være en annen motsatt kraft slik at balansen eksisterer. La oss for eksempel observere vekten som henger fra strengene som vises i følgende figur.

Eksempel på et objekt som er i oversettelses likevekt er at dette veier underlagt taket ved å bruke strengene som er anordnet som vist på bildet. Kilde: f. Zapata.

Vekten forblir i balanse mellom oversettelsen og uten å bevege seg, takket være det vertikale tauet som holder det ved å utøve en spenning T som kompenserer for vekt W. Hver styrke har blitt representert på vest gjennom en pil, hver av like stor størrelse og med samme retning, men motsatt retning.

Kan tjene deg: Isobarisk prosess: Formler, ligninger, eksperimenter, øvelser

Balanseringskraften

Anta at et sett med krefter virker på et objekt. Dette kalles en krefter system hvorav det resulterende kan bli funnet som forklart ovenfor: å legge til hver av systemkreftene vektorly.

Vel, med makt motsatt av dette resultatet kalles balanseringskraft. Hvis den resulterende kraften er F_R Og balanseringskraften er OG, så:

OG + F_R = 0

Derfor:

OG = - F_R

Eksempler på oversettelse likevekt

Mange gjenstander som vi finner daglig, inne og ute av hjemmet, er i oversettelsesbalanse:

Bygninger og veier

Bygninger og veier er bygget for å forbli stabile og ikke snu eller kollapse. I skyskrapere og generelt veldig høye bygninger er imidlertid noe fleksibilitet nødvendig for å motstå vindhandling.

Bøker og gjenstander i hyller

Bøker i et bibliotek og produkter på butikkene er gjenstander som forblir i oversettelsesbalanse og uten å flytte.

Møblene

Møblene, flatskjerm -TV -en og maleriene på veggen, så vel som lampene som henger fra taket, for å nevne noen gjenstander, er i oversettelsesbalanse.

Trafikklysene

Trafikklys er festet med stolper og kabler, slik at de ikke faller. Vi vet imidlertid at vinden får dem til å svinge.

Den offentlige belysningen

Offentlige belysningslys er også i oversettelsesbalanse, fikset på lette innlegg, for eksempel hovedbildet av hovedbildet.

Trening løst

Hvilken størrelse skal styrken ha F_s Statisk friksjon for at boksen i figuren skal forbli i ro midt i det skrå planet en vinkel α på 37º? Massen på boksen er m = 8 kg.

Kan tjene deg: API Gravity: Skala og klassifisering av råolje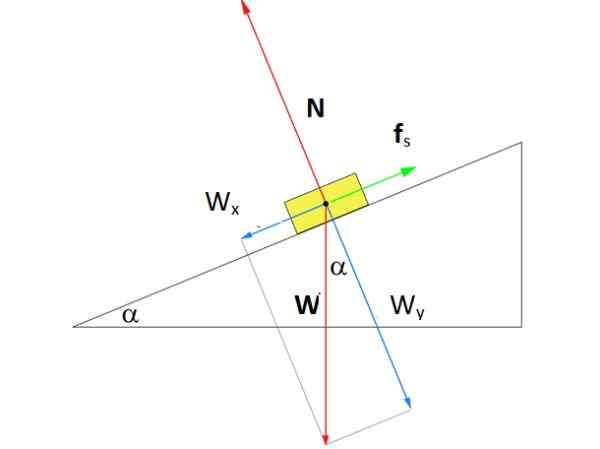Gratis kroppsdiagram for et hvileobjekt på et skrå plan. Kilde: f. Zapata.

Løsning

Figuren viser det frie kroppsdiagrammet på flyet. Det er tre krefter som handler på henne: vekten W, rettet vertikalt nede, det normale N, som er den vinkelrett kraften som utøves av overflaten av planet over boksen, og til slutt den statiske friksjonskraften F_s som motsetter seg boksen for å gli nedoverbakke.

Oversettelsesbalansetilstanden fastslår at:

W + N + F_s = 0

Men du må huske at dette er en vektorsum og å utføre den er nødvendig å dekomponere kreftene til komponenter langs koordinataksene.

I figuren er det trukket et koordinatsystem der x -aksen går parallelt med overflaten av det skrå planet. Med dette valget faller statisk friksjon på denne aksen, mens normalen er på aksen og. Vekten er den eneste kraften som er tilbøyelig, og vi må dekomponere ved hjelp av trigonometri:

W_x = W. sin α
W_og = W. cos α

Summen av krefter gjennom hver akse er:

∑ f_og = N - w_og = 0
∑ f_x = f_s - W_x = 0

Fra denne siste ligningen følger det at:

F_s = W_x

Og som w_x = W. sin α og vektens størrelse på sin side er w = m.g, å være G -verdien av tyngdekraften, så størrelsen på statisk berøring er ganske enkelt:

F_s = m⋅g⋅sen α = 8 kg × 9.8 m/s² × Sen 37º = 47.2 n.

Referanser

1. Bauer, w. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mc Graw Hill.
2. Figueroa, d. (2005). Serier: Fysikk for vitenskap og ingeniørfag. Volum 2. Dynamisk. Redigert av Douglas Figueroa (USB).
3. Giambattista, a. 2010. Fysikk. 2. Ed. McGraw Hill.
4. Serway, r., Jewett, J. (2008). Fysikk for vitenskap og ingeniørfag. Volum 1. 7^ma. Ed. Cengage Learning.
5. Tippens, p. 2011. Fysikk: konsepter og applikasjoner. 7. utgave. McGraw Hill.