Beskrivende statistikkhistorie, egenskaper, eksempler, konsepter

De Beskrivende statistikk Det er grenen av statistikk som omhandler innsamling og organisering av informasjon om atferden til systemer med mange elementer, generisk kjent som navnet på befolkning.

For dette bruker den numeriske og grafiske teknikker, der den presenterer informasjon, uten å komme med spådommer eller slutninger om befolkningen der den kommer.

Den beskrivende statistikken anses å organisere og presentere informasjonen praktisk

[TOC]

Historie

Høy alder

Statistikk har sin opprinnelse i menneskets behov for å organisere nødvendig informasjon for overlevelse og velvære, samt for å sørge for hendelsene som påvirker den. De store sivilisasjonene i antikken forlot poster over nybyggere, samlet skatter, mengden av avlinger og størrelsen på hærene.

For eksempel under sin lange regjeringstid, Ramses II (1279-1213 til.C) Bestilte en folketelling av land og innbyggere i Egypt, som da hadde rundt 2 millioner innbyggere.

På samme måte Bibelen som Moses henrettet en folketelling for å vite hvor mange soldater som hadde de tolv stammene i Israel.

Også i det gamle Hellas ble tellinger av mennesker og ressurser gjort. Romerne, kjent for sin høye organisasjon, registrerte befolkningen med jevne mellomrom og utarbeidet folketellinger hvert femte år, inkludert territorier og ressurser.

Renaissance

Etter nedgangen i Roma var de viktige statistiske postene redd, inntil renessansenes ankomst, når statistikken dukker opp igjen.

Sannsynlighetsteorien ble født, resultatet av folks tilbøyelighet til spill, noe som ga statistikk den matematiske strengeren som gjorde det til en vitenskap i seg selv.

Moderne alder

En ny impuls kom med teorien om feil og minimumsplasser i det nittende århundre, som fulgte metoden for korrelasjon mellom variabler, for å kvantitativt vurdere forholdet mellom dem.

Inntil endelig, i løpet av det tjuende århundre, utvidet statistikken seg til hver gren av vitenskap og ingeniørfag som et uunnværlig verktøy i problemløsning.

Kjennetegn på beskrivende statistikk

Beskrivende statistikk er preget av:

- Organiser informasjon samlet inn i data og grafikk. Grafene kan være forskjellige: histogrammer, frekvenspolygoner, kakeformet diagrammer, blant andre.

- Distribuere data i frekvensområder for å lette ledelsen. Bruk aritmetikk for å finne de mest representative verdiene for dataene, gjennom sentrale tendensmål, samt analysere spredningen av dem.

- Bestem formen på fordelingen, deres symmetri, hvis de er sentrert eller partisk, og hvis de er spiss eller rettere sagt flatet.

Kan tjene deg: implisitte derivater: hvordan de løses og løste øvelser

Hva er beskrivende statistikk for?

Når det er nødvendig.

Så nevner vi noen eksempler:

Økonomi

Beskrivende statistikk omhandler registrering og organisering av data om populasjoner og deres aldre, inntekt, investeringer, overskudd og utgifter. På denne måten planlegger regjeringer og institusjoner forbedringer og investerer på riktig måte.

Med din hjelp overvåker du kjøp, salg, avkastning og effektivitet. Av denne grunn er statistikk uunnværlig i beslutningstaking.

Fysikk og mekanisk

Fysikk og mekanikk bruker statistikk for studier av kontinuerlige medier, som består av et stort antall partikler, for eksempel atomer og molekyler. Det viser seg at det ikke er mulig å overvåke hver av dem hver for seg.

Men å studere den globale oppførselen til systemet (for eksempel en gassdel) fra det makroskopiske synspunktet, er det mulig å finne ut gjennomsnitt og definere makroskopiske variabler for å kjenne dens egenskaper. Et eksempel på dette er den kinetiske teorien om gasser.

Medisin

Det er et essensielt verktøy når du overvåker sykdommer, fra dets opprinnelse og under utviklingen, så vel som effektiviteten av behandlinger.

Statistikken som beskriver frekvensen av sykelighet, helbredelse, inkubasjonstider eller utvikling av en sykdom, alderen der den vanligvis vises og stildata, er nødvendige når du utformer de mest effektive behandlingene.

Ernæring

En av de mange anvendelsene av beskrivende statistikk er å registrere og bestille data om forbruk av mat i de forskjellige befolkningene: deres mengde, kvalitet og som er de mest konsumerte, blant mange andre observasjoner som interesserer eksperter.

Eksempler på beskrivende statistikk

Nedenfor vil vi se noen eksempler som illustrerer hvor nyttige verktøyene i beskrivende statistikk er å bidra til å ta beslutninger:

Eksempel 1

For å forbedre spisestuene på skolen, er det nødvendig med brukerinformasjon. Kilde: Wikimedia Commons.

Utdanningsmyndighetene i en landsplan institusjonelle forbedringer. Anta at de vil implementere et nytt system med spisestuer på skolen.

For dette er det nødvendig å ha data om studentpopulasjonen, for eksempel antall elever per klasse, deres alder, kjønn, høyde, vekt og sosioøkonomisk tilstand. Deretter presenteres denne informasjonen i form av tabeller og grafer.

Eksempel 2

For å overvåke det lokale fotballaget og gjøre nye signeringer, har ledere antallet kamper som ble spilt, vunnet, bundet og tapt, så vel som antall mål, scorere og hvordan de klarte å score: frispark, fra Half Court, straffer, med venstre ben eller høyre, blant andre detaljer.

Det kan tjene deg: gjensidig utelukkende hendelser: egenskaper og eksempler

Eksempel 3

En iskrembutikk har flere smaker av iskrem og ønsker å forbedre salget, derfor gjennomfører eierne en studie der de teller antall kunder, skill dem inn i grupper etter kjønn og aldersspenn.

I denne studien er for eksempel favoritt iskremsmak og den mest solgte presentasjonen. Og med dataene som er samlet inn, planlegger de kjøp av smakene og de nødvendige containere og tilbehør for deres forberedelse.

Grunnleggende konsepter for beskrivende statistikk

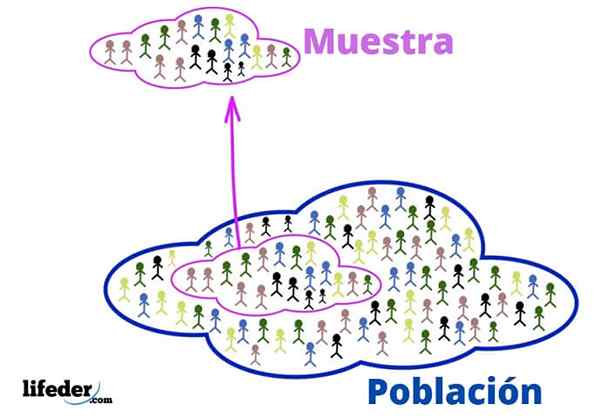Befolkning og prøve

Disse grunnleggende konseptene er nødvendige for å anvende statistiske teknikker, la oss se:

Befolkning

I den statistiske konteksten refererer befolkningen til universet eller kollektivet som informasjonen kommer.

Det handler ikke alltid om mennesker, siden de kan være sett med dyr, planter eller gjenstander som biler, atomer, molekyler og til og med hendelser og ideer.

Prøve

Når befolkningen er veldig stor, blir et representativt utvalg trukket ut fra den og analysert, uten å miste relevant informasjon.

Det kan velges tilfeldig, eller i henhold til noen kriterier som tidligere er etablert av analytikeren. Fordelen er at det å være en delmengde av befolkningen, den er mye mer håndterbar.

Variabel

Det refererer til settet med verdier som kan ta et visst kjennetegn ved befolkningen. En studie kan inneholde forskjellige variabler, for eksempel alder, kjønn, vekt, faglig nivå, sivil status, inntekt, temperatur, farge, tid og mange flere.

Variablene kan være av forskjellig karakter, så det er kriterier for å klassifisere dem og gi dem den mest passende behandlingen.

Kategoriske variabler og numeriske variabler

I henhold til måten de måles, kan variablene være:

-Kategorisk

-Numerisk

De kategoriske variablene, også kalt kvalitativ, De representerer egenskaper som den sivile statusen til en person, som kan være singel, gift, skilt eller enke.

På den annen side, til numeriske variabler eller Kvantitativt, De kan måles, for eksempel alder, tid, vekt, inntekt og mer.

Grafikken er veldig viktig å presentere informasjonen, fordi datetrenden på et øyeblikk blir verdsatt. Kilde: Piqssels.

Diskrete og kontinuerlige variable variabler

Diskrete variabler tar bare diskrete verdier, som navnet tilsier. Eksempler på dem er antall barn av en familie, hvor mange fag som er på et visst kurs og mengden biler på en parkeringsplass.

Disse variablene tar ikke alltid hele verdier, fordi det også er brøkdeler.

På den annen side innrømmer kontinuerlige variabler uendelige verdier innen et visst område, for eksempel vekten til en person, pH i blodet, tiden for en telefonkonsultasjon og diameteren til fotballkulene.

Kan tjene deg: symmetri

Målinger av sentral tendens

Gi en ide om den generelle trenden som dataene følger. Vi vil nevne de tre mest brukte sentrale tiltakene:

-Halv

-Median

-Mote

Halv

Tilsvarer gjennomsnittsverdiene. Det beregnes ved å legge til alle observasjoner og dele mellom det totale antallet:

 Hvor x_Yo Det er enhver observasjon, og n er summen av dem.

Mote

Det er verdien som gjentas mest i et datasett, den hyppigste, siden det i en distribusjon kan være mer enn en måte.

Median

Når du bestiller et datasett, er medianen den sentrale verdien av dem alle.

Målinger av spredning

De påpeker variasjonen av dataene og gir en ide om hvor langt eller spredt de er fra de sentrale tiltakene. De mest brukte er:

Område

Det er forskjellen mellom den største verdien x_M og den minste x_m av et datasett:

Rekkevidde = x_M - x_m

Forskjell

Mål hvor langt gjennomsnittsverdidataene er. For dette er det gjort et gjennomsnitt, men med forskjellene mellom en hvilken som helst verdi x_Yo og gjennomsnittet, kvadratet for å forhindre at de kansellerer hverandre. Det er vanligvis betegnet med den greske bokstaven σ kvadratisk, eller med s²:

Standardavvik

Variansen har ikke de samme enhetene som dataene, så standardavviket er definert som kvadratroten til variansen og er betegnet som σ eller s:

Frekvensfordelinger

I stedet for å ta hensyn til hver data individuelt, er det å foretrekke å gruppere dem i områder, noe som letter arbeidet, spesielt hvis det er mange verdier. Når du for eksempel jobber med barna på en skole, kan de grupperes i aldersområder: fra 0 til 6 år, fra 6 til 12 år og fra 12 til 18 år.

Grafer

De utgjør en utmerket måte å sette pris på fordelingen av en visningsdata, og inneholder all informasjonen samlet i tabellene og bildene, men mye rimeligere.

Det er et bredt utvalg av dem: med barer, lineære, sirkulære, stilk og blad, histogrammer, frekvenspolygoner og piktogrammer. Eksempler på statistiske grafer er presentert i figur 3.

Temaer av interesse

Statistikk grener.

Statistiske variabler.

Befolkning og prøve.

Inferensiell statistikk.

Referanser

1. Faraldo, p. Statistikk og forskningsmetodikk. Gjenopprettet fra: EIO.USC.er.
2. Fernández, s. 2002. Beskrivende statistikk. 2. Utgave. ESIC -redaksjon. Gjenopprettet fra: Google Books.
3. Statistikkhistorie. Gjenopprettet fra: Eumed.nett.
4. Ibañez, p. 2010. Matematikk II. Kompetansetilnærming. Cengage Learning.
5. Monroy, s. 2008. Beskrivende statistikk. 1. Utgave. National Polytechnic Institute of Mexico.
6. Universformler. Beskrivende statistikk. Gjenopprettet fra: Universoformulas.com.