Inferensiell statistikkhistorie, egenskaper, hva er det for, eksempler

De Inferensiell statistikk eller deduktiv statistikk er en som trekker til egenskapene til en populasjon fra prøver hentet ut fra den, gjennom en serie analyseteknikker. Med den innhentede informasjonen blir modeller utdypet som deretter tillater spådommer om oppførselen til nevnte befolkning.

Derfor har inferensiell statistikk blitt den viktigste vitenskapen som tilbyr næring og instrumenter som utallige disipliner krever, når du tar beslutninger.

Fysikk, kjemi, biologi, ingeniørvitenskap og samfunnsvitenskap, og nytte kontinuerlig av disse verktøyene når de lager sine modeller og designer og implementerer eksperimenter.

[TOC]

Kort historie om inferensiell statistikk

Statistikk oppsto i eldgamle tider på grunn av menneskers behov for å organisere ting og optimalisere ressursene. Før oppfinnelsen av skriving ble det gjennomført journal over antall mennesker og husdyr, gjennom symboler som ble registrert i stein.

Senere la kinesiske, babylonske og egyptiske herskere data om mengden avlinger og antall innbyggere, registrert på leirtabletter, søyler og monumenter.

Romerriket

Da Roma utøvde sitt domene i Middelhavet, var det vanlig at myndighetene skulle utføre folketellinger hvert femte år. Faktisk kommer ordet "statistisk" fra det italienske ordet Statista, Hva betyr det å uttrykke.

Parallelt, i Amerika, brakte også de store førkolumbiske imperiene lignende poster.

Middelalderen

I løpet av middelalderen registrerte regjeringene i Europa, så vel som kirken, jordens eiendom. Da gjorde de det samme med fødsler, dåp, ekteskap og dødsfall.

Moderne alder

Den engelske statistikken John Graunt (1620-1674) var den første som kom med spådommer basert på slike lister, for eksempel hvor mange mennesker som kunne dø av visse sykdommer og den estimerte andelen av fødsler av kvinner og menn. Derfor blir faren til demografi vurdert.

Samtidig tidsalder

Senere, med bruk av sannsynlighetsteori, opphørte statistikken å være en samling av organisasjonsteknikker og oppnådde et intetanende omfang som en prediktiv vitenskap.

Dermed var eksperter i stand til.

Kjennetegn

Nedenfor har vi de mest relevante egenskapene til denne grenen av statistikk:

- Inferensiell statistikk studerer en populasjon som tar fra seg et representativt utvalg.

- Eksempelvalget utføres gjennom forskjellige prosedyrer, det mest passende er de som velger komponentene tilfeldig. Dermed har ethvert element i befolkningen samme sannsynlighet for å bli valgt og med det unngås uønskede skjevheter.

Kan tjene deg: Hvordan konvertere fra km/h a m/s? Løste øvelser

- For å organisere informasjonen som er samlet inn, bruker den beskrivende statistikk.

- På utvalget beregnes statistiske variabler som tjener til å estimere egenskapene til befolkningen.

- Inferensiell eller deduktiv statistikk bruker teorien om sannsynligheter for å studere tilfeldige hendelser, det vil si de som oppstår heldigvis. Hver hendelse tildeles en viss sannsynlighet for forekomst.

- Bygg hypoteser - Suposisjoner - Om parametrene til befolkningen og kontrast dem, for å vite om de er riktige eller ikke og beregner også nivået av selvtilliten til responsen, det vil si at det gir en feilmargin. Den første prosedyren kalles Hypotesetester, Mens feilmarginen er konfidensintervall.

Hva er beskrivende statistikk for? applikasjoner

Inferensiell statistikk: essensielt for å ta beslutninger og kvalitetskontroll

Studie i sin helhet en befolkning kan kreve mye ressurser i penger, tid og krefter. Det er å foretrekke å ta representative prøver som er mye mer håndterbare, samle inn data gjennom dem og lage hypoteser eller forutsetninger om prøveatferd.

Når hypotesene er etablert og gyldigheten deres er i kontrast, strekker resultatene seg til befolkningen og brukes til å ta beslutninger.

De er også med på å lage modeller av den befolkningen, for å lage fremtidige anslag. Det er grunnen til at inferensiell statistikk er en veldig nyttig vitenskap for:

Sosiologi og demografiske studier

Dette er ideelle applikasjonsfelt, ettersom statistiske teknikker gjelder med ideen om å etablere forskjellige modeller for menneskelig atferd. Noe som a priori er ganske komplisert, siden mange variabler griper inn.

I politikk brukes mye i valgtid for å kjenne valgmennene, på denne måten partiene designer strategier.

Ingeniørfag

Inferensielle statistikkmetoder er mye brukt i ingeniørfag, de viktigste applikasjonene er kvalitetskontroll og prosesser optimalisering, for eksempel å forbedre tidene i utførelsen av oppgaver, så vel som i forebygging av yrkesulykker.

Økonomi og forretningsadministrasjon 

Med de deduktive metodene kan det utføres anslag om driften av et selskap, det forventede salgsnivået, samt hjelp når du tar beslutninger.

For eksempel kan teknikkene dine brukes til å estimere reaksjonen fra kjøpere til et nytt produkt, i nærheten av å bli lansert til markedet.

Det tjener også til å evaluere hva modifikasjonene i forbruksvanene til mennesker er, gitt viktige hendelser, for eksempel Covid -epidemien.

Eksempler på inferensiell statistikk

Eksempel 1

Et enkelt deduktivt statistisk problem er som følger: En matematikklærer er ansvarlig for 5 deler av elementær algebra på et universitet og bestemmer seg for å bruke gjennomsnittsnotatene til en enkelt av deres seksjoner for å estimere gjennomsnittet av alle.

Kan tjene deg: Omtrentlig måling av amorfe figurer: Eksempel og treningImidlertid kan stor befolkning studeres gjennom et representativt utvalg. Kilde: Pixabay.

En annen mulighet er å ta et utvalg av hver seksjon, studere dens egenskaper og utvide resultatene til alle seksjoner.

Eksempel 2

Manageren for en klesbutikk for damer vil vite hvor mye en viss bluse vil bli solgt i sommersesongen. For å gjøre dette, analyser salg av plagg i løpet av de to første ukene av sesongen og bestemmer dermed trenden.

Grunnleggende konsepter i inferensiell statistikk

Det er flere viktige konsepter, inkludert de som kommer fra sannsynlighetsteori, som er nødvendig for å ha klart for å forstå alt omfanget av disse teknikkene. Noen, som en befolkning og prøve, har vi allerede nevnt gjennom hele teksten.

Begivenhet

En hendelse eller hendelse er noe som skjer, og som kan ha flere resultater. Et hendelseseksempel kan være å starte en valuta, og det er to mulige resultater: ansikt eller forsegling.

Prøveområde

Det er settet med alle mulige resultater av en hendelse.

Befolkning og prøve

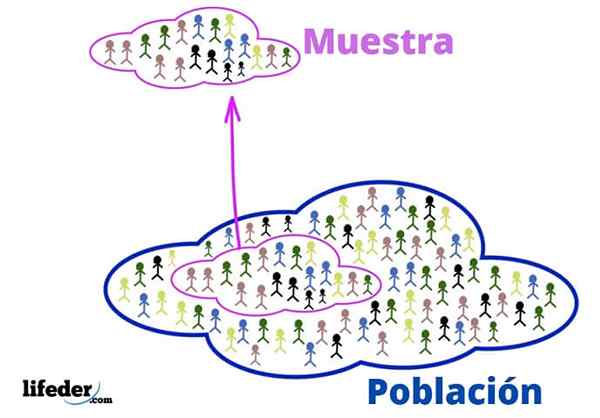Befolkning og prøve

Befolkningen er universet å studere. De handler ikke nødvendigvis om levende mennesker eller vesener, siden befolkningen, i statistikk, kan bestå av objekter eller ideer.

For sin del er prøven en delmengde av befolkningen, hentet fra den nøye for å være representativ.

Prøvetaking

Det er settet med teknikker som en prøve er valgt fra en gitt befolkning. Prøvetaking kan være tilfeldig hvis sannsynlige metoder brukes til å velge prøven, eller ikke probabilistisk, hvis analytikeren har et eget kriterium for utvelgelse, i henhold til deres erfaring.

Statistiske variabler

Sett med verdier som kan ha befolkningens kjennetegn. De er klassifisert på flere måter, for eksempel kan de være diskrete eller kontinuerlige. I henhold til deres natur kan de også være kvalitative eller kvantitative.

Sannsynlighetsfordelinger

Sannsynlighetsfunksjoner som beskriver oppførselen til et stort antall systemer og situasjoner observert i naturen. De mest kjente er Gaussian Distribution eller Gauss Bell og Binomial Distribution.

Parametere og statistikk 

Estimatsteorien slår fast at det er en sammenheng mellom befolkningens verdier og utvalget som er hentet fra den befolkningen. De parametere De er befolkningens kjennetegn som vi ikke vet, men vi vil estimere: for eksempel gjennomsnittet og standardavviket.

For sin del, statistisk er egenskapene til prøven, for eksempel dets gjennomsnittlige og standardavvik.

Anta som et eksempel at befolkningen består av alle unge mellom 17 og 30 år av et samfunn, og det er ønsket å kjenne andelen av de som for tiden er i høyere utdanning. Dette vil være populasjonsparameteren som skal bestemmes.

Kan tjene deg: lineær interpolasjon

For å estimere det, blir et tilfeldig utvalg av 50 ungdommer valgt, og andelen av dem som studerer ved et universitet eller institutt for høyere utdanning, beregnes. Denne andelen er statistikken.

Hvis studien blir utført, bestemmes det at 63 % av de 50 ungdommene studerer høyere, dette er befolkningen estimert, laget av prøven.

Dette er bare et eksempel på hva inferensiell statistikk kan gjøre. Det er kjent som estimat, men det er også teknikker for å forutsi statistiske variabler, samt å ta beslutninger.

Statistisk hypotese

Det er en formodning som er gjort om verdien av gjennomsnittet og standardavviket for noen kjennetegn for befolkningen. Med mindre befolkningen er fullstendig undersøkt, er dette ukjente verdier.

Hypotesetester

Er forutsetningene gjort om populasjonsparametrene gyldige? For å vite det, blir det bekreftet om resultatene fra prøven støtter dem eller ikke, så det er nødvendig å designe hypotesetester.

Dette er de generelle trinnene for å utføre en:

Trinn 1

Identifiser hvilken type distribusjon som befolkningen forventes å følge.

Steg 2

Heve to hypoteser, betegnet som h_enten og h₁. Den første er den nullhypotesen der vi antar at parameteren har en viss verdi. Den andre er Den alternative hypotesen som er en annen verdi enn nullhypotesen. Hvis dette blir avvist, blir den alternative hypotesen akseptert.

Trinn 3

Etablere en akseptabel margin for forskjellen mellom parameteren og statistikken. De vil sjelden være identiske, selv om de forventes å være veldig nærme.

Trinn 4

Foreslå et kriterium for å akseptere eller avvise nullhypotesen. For dette brukes en teststatistikk som kan være gjennomsnittet. Hvis gjennomsnittsverdien er innenfor visse grenser, blir nullhypotesen akseptert, ellers blir den avvist.

Trinn 5

Som et siste trinn avgjøres det om nullhypotesen er akseptert eller ikke.

Temaer av interesse

Statistikk grener.

Statistiske variabler.

Befolkning og prøve.

Beskrivende statistikk.

Referanser

1. Berenson, m. 1985.Statistikk for administrasjon og økonomi, konsepter og applikasjoner. Inter -amerikansk redaksjon.
2. Canavos, g. 1988. Sannsynlighet og statistikk: applikasjoner og metoder. McGraw Hill.
3. Devore, J. 2012. Sannsynlighet og statistikk for ingeniørfag og vitenskap. 8. Utgave. Cengage Learning.
4. Statistikkhistorie. Gjenopprettet fra: Eumed.nett.
5. Ibañez, p. 2010. Matematikk II. Kompetansetilnærming. Cengage Learning.
6. Levin, r. 1981. Statistikk for administratorer. Prentice Hall.
7. Walpole, r. 2007. Sannsynlighet og statistikk for ingeniørfag og vitenskap. Pearson.