Hypotesetesting

Hva er hypotesetest?

De hypotesetesting, I statistikk er det en prosedyre som brukes for å sjekke hvor vellykket er en formodning om en befolkning. Disse formodningene kalles hypotese, at de i prinsippet blir tatt som sanne, inntil noen bevis bekrefter eller benekter det.

Dette beviset leveres av prøvedata, de som kommer fra en betydelig del av befolkningen, kalt prøve. Sannsynlighetsteorien gir de nødvendige teknikkene for å kontrastere hypotesenes sannhet.

Eksempler på hypoteser er:

-Den gjennomsnittlige menneskekroppstemperaturen er 36.1 ºC.

-I gjennomsnitt veier en salt peanøttpose produsert i en snacks -fabrikk 50 g.

-80% av innbyggerne i en by, foretok kjøp på nettet i løpet av de siste 6 månedene.

-IQ -testresultater for universitetsstudenter fra en kjent institusjon, har et standardavvik på 15.

-En viss tilfeldig variabel x følger en Poisson -distribusjon.

De fire første er av typen hypotese parametrisk, Fordi dette er utsagn om noen populasjonsparameter, for eksempel gjennomsnitt, standardavvik eller noen proporsjoner.

På den annen side etablerer den siste hypotesen fordelingen av en tilfeldig variabel, og siden den ikke refererer til noen parameter eller egenskap for befolkningen, sies det at det er en hypotese ikke parametrisk.

Nullhypotese og alternativ hypotese

Det er to typer hypotese å utføre en test, som vil tjene til å kontrastere dem:

-Nullhypotesen, betegnet som h₀, sier at parameteren som er undersøkt har en etablert verdi, eller at den tilfeldige variabelen følger en viss distribusjon. Derfor, ved symbolsk uttrykk for nullhypotesen, brukes alltid symbolet på likestilling.

-Alternativ hypotese: kalt h₁, Han bekrefter at parameteren eller distribusjonen er forskjellig fra hva nullhypotesen sikrer, for å symbolsk uttrykke den alternative hypotesen, symbolene brukes: eller ≠, men aldri likhet.

Det kan tjene deg: eiendom til algebra -lås: demonstrasjon, eksempler

Når nullhypotesen blir akseptert, blir den alternative hypotesen avvist, slik at begge er gjensidig utelukkende.

Nivå av betydning

Det er et mål for feilen som kan gjøres når du utfører en hypotesetest. Det er definert som sannsynligheten for å avvise nullhypotesen, og det er sant. Det er vanligvis betegnet med den greske bokstaven α:

α = p (avvis h₀ Når det er sant)

Verdiene som ofte brukes for α er 0.01, 0.05, og 0.10; å være den andre den hyppigste bruken. Tilsvarende til henholdsvis 1%, 5% og 10% sannsynlighet for å gjøre feil når du avviser h₀, Men i alle fall, jo lavere nivå av betydning, jo mer pålitelig testresultatet.

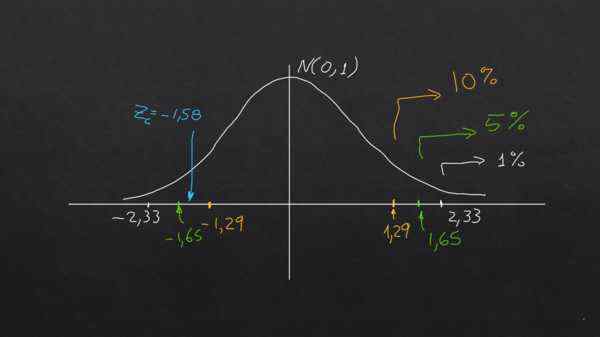
Alfaverdien (α) kan forstås som prosentvis brøkdel av høyre hale (eller venstre) område, i en normalfordeling som er karakterisert (μ = 0 og σ = 1) og disse verdiene forekommer alltid ved z = 2,33 for α = 0.01; ved z = 1,65 for α = 1,65 og ved z = 1,29 for α = 0,1.

Trinn for å utføre en hypotesetest

Trinn 1

Definer henholdsvis null og alternative hypoteser. Nullhypotesen slår fast at parameteren som studeres, kalt θ, er lik en referanseverdi, betegnet som θ₀:

H₀: θ = θ₀

For eksempel, hvis effekten av et medikament blir undersøkt på et visst kjennetegn på en populasjon av laboratoriemus, vurderer nullhypotesen at dette stoffet ikke gjør noen forskjell i en slik karakteristikk, og at dette har en konstant verdi θ₀.

For å symbolisere nullhypotesen, brukes likestillingstegnet alltid, derimot, den alternative hypotesen benytter seg av et av symbolene eller ≠.

I eksemplet med stoffet fastslår den alternative hypotesen at forbindelsen har en viss effekt på det aktuelle karakteristikken. Derfor er dette større, lavere eller bare forskjellig fra referanseverdien θ₀.

Kan tjene deg: Faktoriell notasjon: Konsept, eksempler og øvelser

Steg 2

Velg passende nivå av betydning, som vanligvis er etablert til 5 %, som tidligere angitt.

Trinn 3

Bestem populasjonen og trekke fra den prøven, eller prøver, hvis analyse vil tjene til å kontrastere hypotesene og bestemme aksept eller avvisning av nullhypotesen.

Trinn 4

Velg og beregne verdien av prøvestatistikken for dataene som er samlet inn, hvor de nødvendige bevisene er innhentet for å ta beslutningen om å akseptere eller avvise nullhypotesen. Valget av prøvestatistikken avhenger av den valgte parameteren: gjennomsnitt, avvik, andel eller annet.

Prøvestatistikken oppnås ved å konvertere en prøveparameter til en Z -poengsum, en student, R Pearson eller Chi Square -statistikk, ifølge den valgte eksperimentelle designen. Det er formler for dette.

Vanligvis, hvis populasjonsparameteren er den gjennomsnittlige μ, "x bar" er prøvegjennomsnittet, er standardavviket σ kjent og prøvestørrelsen er n> 30, teststatistikken z_C Det beregnes med Z -poengsummen:

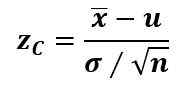
Og når n < 30, pero σ es desconocida, se usa la t de Student.

Trinn 5

Etablere kriterier for aksept eller avvisning av nullhypotesen, som kan gjøres gjennom to prosedyrer:

• Gjennom p -verdier.
• I sammenligning med kritiske verdier.

P -verdier tilsvarer sannsynligheten for å oppnå resultatene som er funnet, siden nullhypotesen er sann. Hvis disse verdiene er små, blir nullhypotesen avvist, hvis de ikke er det, aksepteres den. I alle fall utgjør P -verdier ikke beviset på at den alternative hypotesen er sann.

Det bør tas i betraktning at det i en hypotesetest er mulig å lage to typer feil:

• Type I -feil: Avvis h₀ Når det er sant. Sannsynligheten er α og tilsvarer bevisets betydningsnivå.
• Type II feil: Godta h₀ Når det faktisk er usant. Sannsynligheten er betegnet som β.

Det kan tjene deg: Hva er forholdet mellom Rhombus -området og rektangelet?

Trinn 6

Ta beslutningen om å godta eller avvise nullhypotesen. Hvis verdiene til P brukes, når P < α, se rechaza H₀ Og H aksepteres₁, Og ellers aksepteres H₀. Settet med P -verdier < α se conoce como Kritisk region. Hvis statistikken er i dette intervallet, blir h avvist₀.

Tilsvarende velges en kritisk verdi, i henhold til den valgte populasjonsparameteren. Hvis dette er gjennomsnittet, fortsett som følger:

• Test av en hale: θ < θ₀ eller θ> θ₀
• To haler Test: | θ | < θ₀

Løst eksempel

En maskin produserer skruer hvis nominell verdi må være 800 millimeter lang, med et standardavvik på 5%.

Det tas en tilfeldig prøve, det vil si på forskjellige dager av produksjonsuken, som utgjør omtrent 40 skruer. Når den gjennomsnittlige lengden på prøven beregnes, oppnås 790 millimeterverdi.

Bestem om gjennomsnittlig lengde er i henholdsvis toleranse med nivåer av betydning på 1%, 5% og 10%.

Løsning

Den første er å beregne den gjennomsnittlige teststatistikken, som i dette tilfellet er avviket fra det delte gjennomsnittet mellom standard populasjonsfeil:

ZC = (790 - 800) / (40 / √40) = -1,58

Der det er tatt i betraktning at 5% standardavvik tilsvarer 40 av 800.

Nullhypotesen er at den gjennomsnittlige prøven er innenfor den toleransen som er tillatt til det nødvendige nivået av betydning, forutsatt at | Zc | er mindre enn den karakteriserte verdien | ZT |, ellers blir nullhypotesen avvist.

For 1% og 5% betydning blir nullhypotesen oppfylt, siden | ZC | < 2,33 y |Zc| < 1,65 respectivamente.

For 10% betydning hender det imidlertid at | Zc | > 1.29. Det vil si at på dette nivået av betydning er nullhypotesen ikke oppfylt.

Følgende graf tydeliggjør konklusjonen:

Grafen viser som avhengig av nivået av betydning som kreves den samme hypotesen kan aksepteres eller avvises med de samme dataene. Kilde: f. Zapata.