Absolutt frekvensformel, beregning, distribusjon, eksempel

De Absolutt fresuens Det er definert som antall ganger at de samme dataene gjentas i settet med observasjoner av en numerisk variabel. Summen av alle absolutte frekvenser tilsvarer totalt data.

Når det er mange verdier av en statistisk variabel, er det praktisk å organisere dem ordentlig for å hente ut informasjon om deres oppførsel. Slik informasjon er gitt av sentrale tendensmål og spredningstiltak.

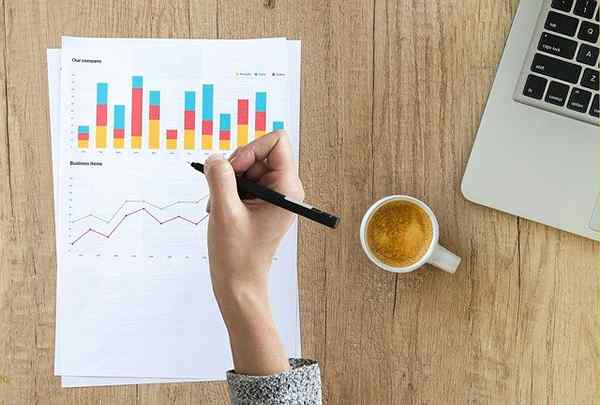
Figur 1. Den absolutte frekvensen av en statistisk observasjon er nøkkelen til å finne trenden som følger datasettet

I beregningene av disse tiltakene er dataene representert gjennom frekvensen de vises i alle observasjonene.

Følgende eksempel viser hvordan å avsløre den absolutte frekvensen av hver data er. I løpet av første halvdel av mai var dette størrelsene på best -selgende cocktail -kostymer, av et kjent dameklær lager:

8; 10; 8; 4; 6; 10; 12; 14; 12; 16; 8; 10; 10; 12; 6; 6; 4; 8; 12; 12; 14; 16; 18; 12; 14; 6; 4; 10; 10; 18

Hvor mange kjoler selges i en bestemt størrelse, for eksempel størrelse 10? Eiere er interessert i å vite å bestille.

Å bestille dataene er enklere å telle, det er nøyaktig 30 observasjoner totalt enn bestilt fra de minste til de høyeste er slik:

4; 4; 4; 6; 6; 6; 6; 8; 8; 8; 8; 10; 10; 10; 10; 10; 10; 12; 12; 12; 12; 12; 12; 14; 14; 14; 16; 16; 18; 18

Og nå er det tydelig at størrelse 10 gjentas 6 ganger, derfor er den absolutte frekvensen lik 6. Den samme prosedyren utføres for å finne ut den absolutte frekvensen av de gjenværende størrelsene.

[TOC]

Formler

Den absolutte frekvensen, betegnet som f_Yo, Det er lik antall ganger som en viss x -verdi_Yo er innenfor gruppen av observasjoner.

Forutsatt at de totale observasjonene er av N -verdier, må summen av alle absolutte frekvenser være lik nevnte antall:

Kan tjene deg: papomudas

∑f_Yo = f₁ + F₂ + F₃ +... f_n = N

Andre frekvenser

Hvis hver verdi av f_Yo Det er delt på det totale antallet data n, du har relativ frekvens F_r av verdi x_Yo:

F_r = f_Yo / N

Relative frekvenser er verdier mellom 0 og 1, fordi n alltid er større enn noen f_Yo, Men summen må være lik 1.

Multipliser med 100 til hver verdi av f_r du har Relativ prosentfrekvens, hvis sum er 100%:

Relativ prosentfrekvens = (f_Yo / N) x 100%

Det er også viktig akkumulert frekvens F_Yo Inntil en viss observasjon, er dette summen av alle absolutte frekvenser inntil nevnte observasjon inkludert:

F_Yo = f₁ + F₂ + F₃ +... f_Yo

Hvis den akkumulerte frekvensen er delt med det totale antallet data n, har du akkumulert relativ frekvens, som multiplisert per 100 resulterer i akkumulert relativ frekvensprosent.

Hvordan få den absolutte frekvensen?

For å finne den absolutte hyppigheten av en viss verdi som tilhører et datasett, er alle organisert fra minst til størst og verdien telles.

I eksemplet på størrelsene på kjolene er den absolutte frekvensen av størrelse 4 3 kjoler, det vil si F₁ = 3. For størrelse 6 ble 4 kjoler solgt: f₂ = 4. I størrelse 8 4 kjoler ble også solgt, f₃ = 4 og så videre.

Tabulering

De totale resultatene kan være representert i en tabell som viser de absolutte frekvensene for hver:

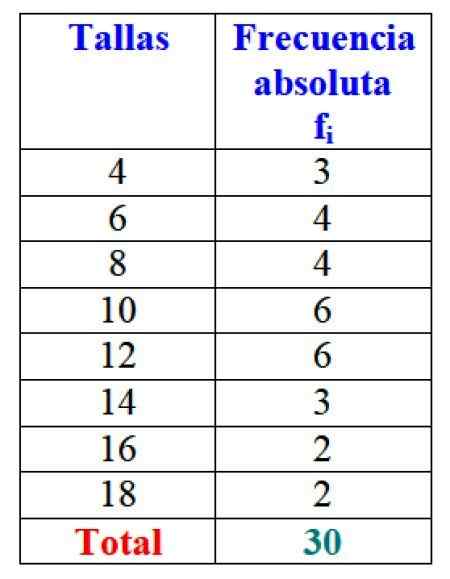Figur 2. Tabell som representerer den variable "solgte salg" og de respektive absolutte frekvensene. Kilde: f. Zapata.

Det er klart det er fordelaktig å bestille informasjonen og kunne få tilgang til den, i stedet for å jobbe med løse data.

Viktig: Merk at ved å legge til alle verdiene i kolonne F_Yo  Det totale antallet data oppnås alltid. Hvis ikke, må regnskapsføringen gjennomgås, siden det er en feil.

Utvidet frekvensbord

Den forrige tabellen kan utvides ved å legge til de andre typene frekvens i påfølgende kolonner til høyre:

Kan tjene deg: homokedastisitet: hva er, viktighet og eksempler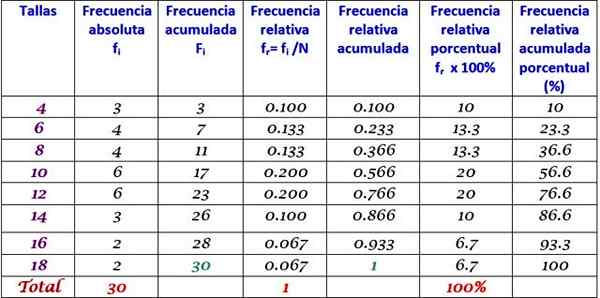

Frekvensfordeling

Frekvensfordeling er resultatet av organisering av data når det gjelder frekvensene deres. Når du jobber med mange data, er det praktisk å gruppere dem i kategorier, intervaller eller klasser, hver med sine respektive frekvenser: absolutte, relative, akkumulerte og prosentvise.

Målet med å gjøre dem er lettere å få tilgang til informasjonen som dataene inneholder, samt tolke dem ordentlig, noe som ikke er mulig når de blir presentert uten orden.

I eksemplet på størrelsene er ikke dataene gruppert, siden de ikke er for mange størrelser og lett kan manipuleres og telles. Kvalitative variabler kan også arbeides på denne måten, men når dataene er veldig mange, jobber de bedre å gruppere dem i klasser.

Frekvensfordeling for grupperte data

For å gruppere dataene i klasser av samme størrelse, må følgende vurderes:

-Størrelse, bredde eller klasseamplitude: Det er forskjellen mellom klassens største verdi.

Klassestørrelse avgjøres ved å dele området R med antall klasser som skal vurderes. Området er forskjellen mellom den maksimale verdien av dataene og den mindreårige, som dette:

Klassestørrelse = utvalg / antall klasser.

-Klassegrense: intervall som går fra den nedre grensen til den øvre grensen i klassen.

-Klassemerke: Det er midtpunktet i intervallet, som regnes som representativ for klassen. Det beregnes med semi -limit av den øvre grensen og den nedre grensen for klassen.

-Antall klasser: Sturges formel kan brukes:

Klasser = 1 + 3.322 log n

Hvor n er antall klasser. Som vanligvis er et desimaltall, er følgende avrundet.

Eksempel

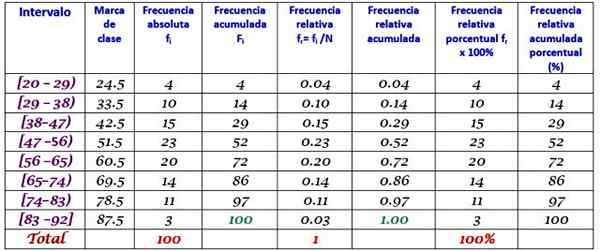
En stor fabrikkmaskin er ute av drift, siden den har tilbakevendende feil. De påfølgende periodene med inaktivitet på få minutter, av nevnte maskin, er registrert nedenfor, med totalt 100 data:

Det kan tjene deg: Frekvens sannsynlighet: Konsept, hvordan det beregnes og eksempler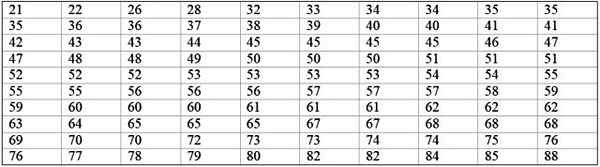

Først bestemmes antall klasser:

Klasser = 1 + 3,322 log n = 1 + 3.32 log 100 = 7.64 ≈ 8

Klassestørrelse = område / antall klasser = (88-21) / 8 = 8.375

Det er også et desimaltall, så det tar 9 som klassestørrelse.

Klassemerket er gjennomsnittet mellom den øvre og nedre grensen for klassen, for eksempel for klasse [20-29) Det er et merke av:

Klassemerke = (29 + 20) / 2 = 24.5

Fortsett på samme måte for å finne klassemerkene i de gjenværende intervallene.

Trening løst

40 unge indikerte at tiden på få minutter som gikk på internett forrige søndag var den neste, bestilte i økende grad:

0; 12; tjue; 35; 35; 38; 40; Fire fem; 45, 45; 59; 55; 58; 65; 65; 70; 72; 90; 95; 100; 100; 110; 110; 110; 120; 125; 125; 130; 130; 130; 150; 160; 170; 175; 180; 185; 190; 195; 200; 220.

Det blir bedt om å bygge frekvensfordelingen av disse dataene.

Løsning

Rangering av settet med n = 40 data er:

R = 220 - 0 = 220

Bruken av Sturges -formelen for å bestemme antall klasser gir følgende resultat:

Klasser = 1 + 3,322 log n = 1 + 3.32 Log 40 = 6.3

Som en desimal er den umiddelbare helheten 7, derfor er dataene gruppert i 7 klasser. Hver klasse har en bredde på:

Klassestørrelse = område / antall klasser = 220/7 = 31.4

En nær og rund verdi er 35, derfor velges en klassebredde på 35.

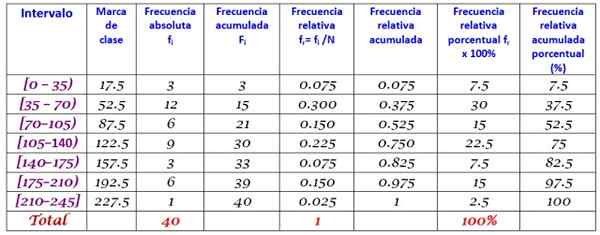
Klassemerker beregnes i gjennomsnitt den øvre og nedre grensen for hvert intervall, for eksempel for intervallet [0,35):

Klassemerke = (0+35)/2 = 17.5

Vi fortsetter på samme måte med de gjenværende klassene.

Til slutt beregnes frekvensene i henhold til prosedyren beskrevet ovenfor, noe som resulterer i følgende distribusjon:

Referanser

1. Berenson, m. 1985. Statistikk for administrasjon og økonomi. Inter -American s.TIL.
2. Devore, J. 2012. Sannsynlighet og statistikk for ingeniørfag og vitenskap. 8. Utgave. Cengage.
3. Levin, r. 1988. Statistikk for administratorer. 2. Utgave. Prentice Hall.
4. Spiegel, m. 2009. Statistikk. Schaum -serien. 4 ta. Utgave. McGraw Hill.
5. Walpole, r. 2007. Sannsynlighet og statistikk for ingeniørfag og vitenskap. Pearson.