Akkumulert frekvensformel, beregning, distribusjon, eksempler

De akkumulert frekvens Det er summen av absolutte frekvenser f, fra barnet som tilsvarer en viss verdi av variabelen. På sin side er den absolutte frekvensen antall ganger en observasjon vises i datasettet.

Åpenbart må studievariabelen være ordnet. Og ettersom den akkumulerte frekvensen oppnås ved å legge til de absolutte frekvensene, viser det seg at den akkumulerte frekvensen til de siste dataene må sammenfalle med det totale antallet av dem. Ellers er det en feil i beregningene.

Den akkumulerte frekvensen brukes til styring av statistiske data

Generelt sett er den akkumulerte frekvensen betegnet som f_Yo (Eller noen ganger n_Yo), for å skille det fra den absolutte frekvensen f_Yo og det er viktig å legge til en kolonne for den i tabellen som dataene er organisert med, kjent som Frekvensbord.

På denne måten blir det forenklet blant annet å holde beretningen om hvor mange data som ble talt til en viss observasjon.

A f_Yo Det er også kjent som Absolutt akkumulert frekvens. Hvis du deler mellom de totale dataene, har du Relativ akkumulert frekvens, hvis endelige sum må være lik 1.

[TOC]

Formler

Den akkumulerte frekvensen av en viss verdi av variabel x_Yo  Det er summen av de absolutte frekvensene f av alle verdier lavere enn eller lik den:

F_Yo  = f₁ + F₂ + F₃  +... f_Yo

Ved å legge til alle absolutte frekvenser oppnås det totale antallet data n, det vil si:

F₁ + F₂ + F₃ +.. . + F_n = N

Den forrige operasjonen er skrevet på en kortfattet måte av sumsymbolet ∑:

∑ f_Yo = N

Andre akkumulerte frekvenser

Følgende frekvenser kan også akkumuleres:

-Relativ frekvens: Det oppnås ved å dele den absolutte frekvensen f_Yo Mellom de totale dataene n:

F_r = f_Yo / N

Hvis de relative frekvensene legges til fra barnet til den som tilsvarer en viss observasjon, er akkumulert relativ frekvens. Den siste verdien må være lik 1.

-Akkumulert akkumulert frekvensprosent: Den akkumulerte relative frekvensen per 100% multipliseres.

F_% = (f_Yo / N) x 100%

Disse frekvensene er nyttige for å beskrive dataatferd, for eksempel ved å finne sentrale tendensmål.

Hvordan få den akkumulerte frekvensen?

For å få den akkumulerte frekvensen er det nødvendig å bestille dataene og organisere dem i en frekvensbord. Prosedyren er illustrert i følgende praktiske situasjon:

Kan tjene deg: sammensatt suksess

-I en nettbutikk som selger mobiltelefoner, salgsrekorden for et bestemt merke i mars måned, følgende verdier per dag:

1; 2; 1; 3; 0; 1; 0; 2; 4; 2; 1; 0; 3; 3; 0; 1; 2; 4; 1; 2; 3; 2; 3; 1; 2; 4; 2; 1; 5; 5; 3

Variabelen er Antall telefoner som selges om dagen Og det er kvantitativt. Dataene som presenteres er ikke så enkle å tolke, for eksempel kan eierne av butikken være interessert i.

Informasjon som dette og mer, det kan fås ved å presentere dataene på en ordnet måte og spesifisere frekvensene.

Hvordan fylle frekvensbordet

For å beregne den akkumulerte frekvensen bestilles dataene:

 0; 0; 0; 0; 1; 1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 2; 2; 2; 2; 3; 3; 3; 3; 3; 3; 4; 4; 4; 5; 5

Deretter bygges en tabell med følgende informasjon:

-Den første kolonnen til venstre med mengden solgte telefoner, mellom 0 og 5 og i økende bestilling.

-Andre kolonne: Absolutt frekvens, som er antall dager som ble solgt 0 telefoner, 1 telefon, 2 telefoner og så videre.

-Tredje kolonne: Den akkumulerte frekvensen, bestående av summen av forrige frekvens pluss frekvensen av dataene som skal vurderes.

Denne kolonnen begynner med den første kolonnen i den absolutte frekvenskolonnen, i dette tilfellet er den 0. For neste verdi legges dette til med forrige. Dermed videreføres de siste dataene fra den akkumulerte frekvensen, som må sammenfalle med de totale dataene.

Tabell over fresning

Følgende tabell viser variabelt "Antall telefoner som selges på en dag", dens absolutte frekvens og den detaljerte beregningen av dens akkumulerte frekvens.

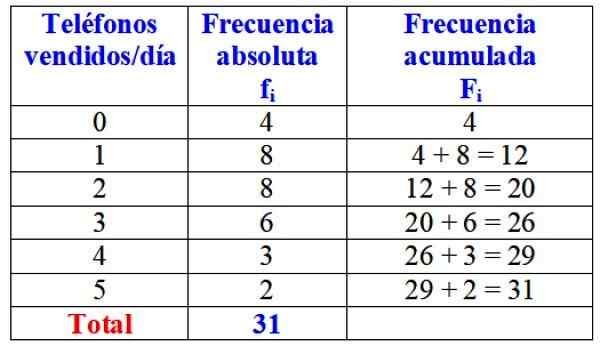Tabell over absolutte og akkumulerte frekvenser for variabelen "Selges telefoner per dag". Kilde: f. Zapata.

I første øyekast kan det sies at det aktuelle merket nesten alltid selges en eller to telefoner per dag, siden den mest absolutte frekvensen er 8 dager, noe som tilsvarer disse verdiene på variabelen. Bare i 4 dager i måneden solgte ikke en eneste telefon.

Det kan tjene deg: trigonometriske grunner: eksempler, øvelser og applikasjoner

Som nevnt er det lettere å undersøke tabellen enn de løse dataene som opprinnelig ble samlet inn.

Akkumulert frekvensfordeling

En akkumulert frekvensfordeling er en tabell der absolutte frekvenser, akkumulerte frekvenser, akkumulerte relative frekvenser og akkumulerte prosentfrekvenser er tilgjengelige.

Selv om fordelen med å organisere dataene i en tabell som den forrige blir lagt merke til, er det veldig stort å organisere dem som vist ovenfor, fordi hvis mange frekvenser vises, er det mulig å tolke.

Problemet kan være liggende ved å bygge a Frekvensfordeling Med intervaller, en nyttig prosedyre når variabelen tar et stort antall verdier, eller hvis det er en kontinuerlig variabel.

Her er verdiene gruppert i intervaller med lik amplitude, kalt klasse. Klassene er preget av å ha:

-Klassegrense: er de ekstreme verdiene for hvert intervall, det er to, den øvre grensen og den nedre grensen. Generelt hører ikke den øvre grensen til intervallet, men til det umiddelbare følgende, mens den nedre grensen hører hjemme.

-Klassemerke: Det er midtpunktet i hvert intervall, og blir tatt som den representative verdien av det.

-Klassebredde: Det beregnes ved å trekke fra verdien av hoved- og den minste (området) og dele med antall klasser:

Klassebredde = område / antall klasser

Da er utdypingen av frekvensfordelingen detaljert.

Eksempel

Dette datasettet tilsvarer 40 karakterer av en matematikkeksamen, på skalaen fra 0 til 10:

0; 0; 0; 1; 1; 1; 1; 2; 2; 2; 3; 3; 3; 3; 4; 4; 4; 4; 5; 5; 5; 5; 6; 6; 6; 6; 7; 7; 7; 7; 7; 7; 8; 8; 8; 9; 9; 9; 10; 10.

En frekvensfordeling med en viss mengde klasser kan utvikles, for eksempel 5 klasser. Det må huskes at når du bruker mange klasser, er dataene ikke lett å tolke, og følelsen av å utføre gruppen er tapt.

Kan tjene deg: Hvor mye må du legge til 3/4 for å få 6/7?

Og hvis de tvert imot er gruppert i veldig få, så blir informasjonen utvannet og en del av den går tapt. Alt avhenger av mengden data du har.

I dette eksemplet er det en god idé å ha to score i hvert intervall, siden det er 10 score og 5 klasser vil bli opprettet. Rangeringen er subtraksjonen mellom majoren og den minste vurderingen, klassebredden er:

Klassebredde = (10-0)/5 = 2

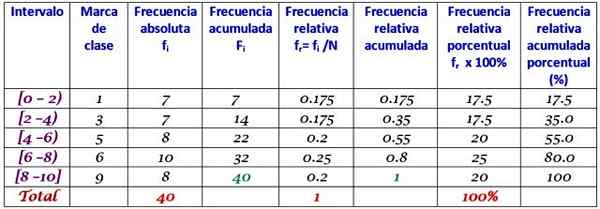
Intervallene er lukket ved venstre og åpne til høyre (unntatt den siste), som er symbolisert med henholdsvis firkantede parentes og parenteser. Alle har samme bredde, men det er ikke obligatorisk selv om den hyppigste.

Hvert intervall inneholder en viss mengde elementer eller absolutt frekvens, og i den følgende kolonnen er den akkumulerte frekvensen, der summen bæres. Tabellen viser også den relative frekvensen F_r  (Absolutt frekvens mellom det totale antall data) og prosentvis frekvensprosent F_r × 100%.

Foreslått trening

Et selskap ringte daglige samtaler til sine kunder i løpet av de to første månedene av året. Dataene er som følger:

6, 12, 7, 15, 13, 18, 20, 25, 12, 10, 8, 13, 15, 6, 9, 20, 24, 12, 7, 10, 11, 13, 9, 12, 15, 18, 20, 13, 17, 23, 25, 14, 18, 6, 14, 16, 9, 6, 10, 12, 13, 17, 14, 26, 7, 12, 24, 7, 7

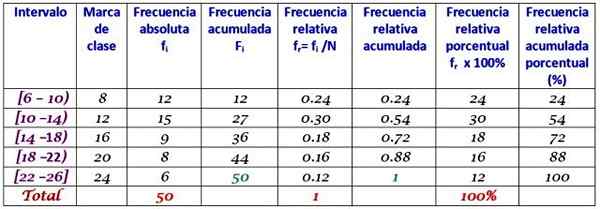
Gruppe i 5 klasser og bygg bordet med frekvensfordelingen.

Svar

Klassebredden er:

(26-6)/5 = 4

Prøv å løse det før du ser svaret.

Referanser

1. Berenson, m. 1985. Statistikk for administrasjon og økonomi. Inter -American s.TIL.
2. Devore, J. 2012. Sannsynlighet og statistikk for ingeniørfag og vitenskap. 8. Utgave. Cengage.
3. Levin, r. 1988. Statistikk for administratorer. 2. Utgave. Prentice Hall.
4. Sannsynlighet og statistikk. Klasseintervallbredde. Retrieved from: Pedroprobabability and Stadistic.Blogspot.com.
5. Spiegel, m. 2009. Statistikk. Schaum -serien. 4 ta. Utgave. McGraw Hill.
6. Walpole, r. 2007. Sannsynlighet og statistikk for ingeniørfag og vitenskap. Pearson.