Bijektive funksjon Hva er, hvordan gjøres det, eksempler, øvelser
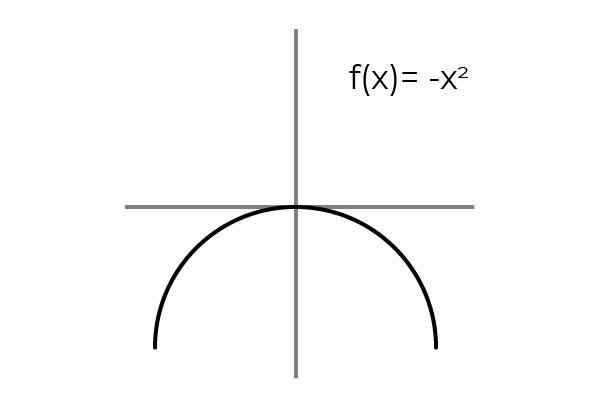
- 4831
- 424
- Jonathan Moe
EN Bijektivfunksjon Det er en som oppfyller den doble tilstanden til å være Injiserende og oversvivende. Det vil si at alle elementene i domenet har et enkelt bilde i kodominiet, og i sin tur er codominium lik funksjonsområdet (funksjonen ( RF ).
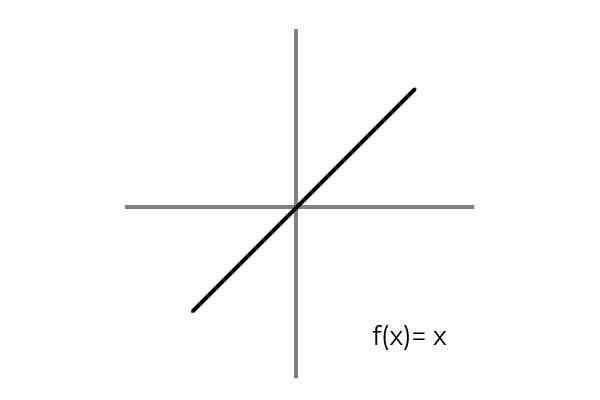
Det blir oppfylt når et biunivokalt forhold mellom elementene i domene og kodominium vurderes. Et enkelt eksempel er funksjonen F: r → R definert av linjen F (x) = x
 Kilde: Forfatter
Kilde: Forfatter Det observeres at for hver verdi av domenet eller avgangssettet (begge begrepene gjelder likt) er det et enkelt bilde i codominium eller ankomstsett. I tillegg er det ikke noe element av codominium som ikke er bilde.
Dermed F: r → R definert av linjen F (x) = x er bijektiv
[TOC]
Hvordan er en bijjektiv funksjon?
For å svare på dette er det nødvendig å ha klare konsepter relatert til Injektivitet og Overvisning av en funksjon, I tillegg til kriteriene for kondisjoneringsfunksjoner for å tilpasse dem til kravene.
Injeksjon av en funksjon
En funksjon er Injeksjon Når hvert av elementene i dets domene er relatert til et enkelt element av codominium. Et element av kodominium kan bare være et bilde av et enkelt element i domenet, på denne måten kan ikke verdiene til den avhengige variabelen gjentas.
Å overveie Injeksjon Følgende må oppfylles til en funksjon:
∀ x1 ≠ x2 ⇒ F (x1 ) ≠ f (x2 )
Overvisning av en funksjon
En funksjon er klassifisert som Overvirkende, Hvis hvert element i kodominiet er et bilde av minst ett domeneelement.
Å overveie Overvirkende Følgende må oppfylles til en funksjon:
Kan tjene deg: erstatningsprøvetakingVære F: dF → CF
∀ B ℮ CF OG til ℮ DF / F (a) = b
Dette er den algebraiske måten å fastslå det for hver "B" som tilhører CF Det er en "A" som tilhører DF slik at funksjonen evaluert i "A" er lik "B".
Kondisjonering av funksjoner
Noen ganger en funksjon som ikke er Bijektiv, kan gjennomgå en viss kondisjonering. Disse nye forholdene kan gjøre det til en Bijektivfunksjon. Alle typer modifikasjoner av funksjonen og kodominiet til funksjonen er gyldig.
Eksempler: Løste øvelser
Oppgave 1
Være funksjonen F: r → R definert av linjen F (x) = 5x +1
A: [Alle reelle tall]
Det observeres at for enhver domeneverdi er det et bilde i codominium. Dette bildet er unikt, noe som lager F vær en Injeksjonsfunksjon. På samme måte observerer vi at kodominiet til funksjonen er lik dets område. Dermed oppfylle tilstanden til Overvisning.
Å være injiserende og overvirkende samtidig som vi kan konkludere med det
F: r → R definert av linjen F (x) = 5x +1 er en Bijektivfunksjon.
Dette gjelder alle lineære funksjoner (funksjoner hvis større grad av variabelen er en).
Oppgave 2
Være funksjonen F: r → R definert av F (x) = 3x2 - 2
Når du tegner en horisontal linje, observeres det at grafen finnes ved mer enn én anledning. På grunn av dette funksjonen F Det er ikke injiserende, og derfor vil det ikke være Bijektiv Mens du blir definert i R → R
På samme måte er det codominium -verdier som ikke er bilder av noe domeneelement. På grunn av dette er ikke funksjonen overbevisst, som også fortjener å kondisjonere ankomstsettet.
Kan tjene deg: sett teori: egenskaper, elementer, eksempler, øvelserDomenet og kodominiet til funksjonen er betinget av
F: [0 , ∞] → [ - 2 , ∞ ]
Der det observeres at det nye domenet dekker verdier fra null til positiv uendelig. Unngå repetisjon av verdier som påvirker injeksjonen.
Dermed er kodominiet blitt modifisert, og teller fra "-2" til den positive uendelig, og eliminerer fra kodominiet verdiene som ikke tilsvarte noe domeneelement
På denne måten kan det sikres at F : [0 , ∞] → [ - 2 , ∞ ] definert av F (x) = 3x2 - 2
Det er bijektiv
Øvelse 3
Være funksjonen F: R → R definert av F (x) = sin (x)
I intervallet [ -∞ , +∞ ] Bihulefunksjonen varierer resultatene mellom null og ett.
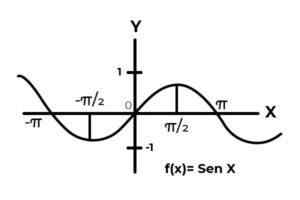 Kilde: Forfatter.
Kilde: Forfatter. Funksjonen F Det samsvarer ikke med injeksjons- og overvisningskriteriene, fordi de avhengige variableverdiene gjentas hvert π -intervall. I tillegg vil vilkårene for kodominiet utenfor intervallet [-eleven] De er ikke bilde av noe domeneelement.
Når du studerer funksjonsgrafikken F (x) = sin (x) intervaller blir observert der oppførselen til kurven oppfyller kriteriene for Bijektivitet. Slik som intervallet DF = [ π/2,3π/2 ] For domene. OG CF = [-1, 1] For codominium.
Der funksjonen varierer fra 1 til -1, uten å gjenta noen verdi i den avhengige variabelen. Og samtidig er co -roominium lik verdiene som er brukt av uttrykket Sin (x)
På denne måten funksjonen F: [ π/2,3π/2 ] → [-1, 1] definert av F (x) = sin (x). Det er bijektiv
Oppgave 4
Hev de nødvendige betingelsene for DF og cF. Slik at uttrykket
Kan tjene deg: Prøvetakingsfeil: Formler og ligninger, beregning, eksemplerF (x) = -x2 Være bijing.
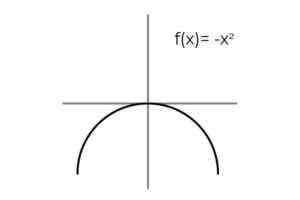 Kilde: Forfatter
Kilde: Forfatter Gjentakelsen av resultatene blir observert når variabelen tar motsatte verdier:
F (2) = f (-2) = -4
F (3) = f (-3) = -9
F (4) = f (-4) = -16
Domenet er betinget, og begrenser det til høyre side av den virkelige linjen.
DF = [0 , +∞ ]
På samme måte observeres det at området for denne funksjonen er intervallet [ -∞ , 0], som ved å tjene som kodominium oppfyller betingelsene for overvisning.
På denne måten kan vi konkludere med det
Uttrykket F: [0 , +∞ ] → [ -∞ , 0] definert av F (x) = -x2 Det er bijektiv
Foreslåtte øvelser
Kontroller om følgende funksjoner er bijektive:
F: [0 , ∞) → R definert av F (x) = 3 (x + 1)2 +2
F: [ 3π/2,5π/2 ] → R definert av F (x) = 5ctg (x)
F: [ -π,π ] → R definert av F (x) = cos (x - 3)
F: r → R definert av linjen F (x) = -5x + 4
Referanser
- Introduksjon til logikk og kritisk tenking. Merrilee h. Laks. University of Pittsburgh
- Problemer i matematisk analyse. Piotr Bilar, Alfred Witkowski. University of Wroclaw. Stang.
- Elementer av abstrakt analyse. Mícheál O'Searcoid PhD. Institutt for matematikk. University College Dublin, Beldfield, Dublind 4
- Introduksjon til logikk og til metodikken til de deduktive vitenskapene. Alfred Tarski, New York Oxford. Oxford University Press.
- Matematiske analyseprinsipper. Enrique Linés Escardó. Redaksjonell tilbakevending. Til 1991. Barcelona, Spania.
- « Glykogenstruktur, syntese, nedbrytning, funksjoner
- Karakteristiske enzymeregenskaper, handlingsmekanismer, eksempler »

