Logaritmiske funksjonsegenskaper, eksempler, øvelser

De logaritmisk funksjon Det er et matematisk forhold som forbinder hvert positivt reelt tall x Med logaritmen din og på en base til. Dette forholdet oppfyller kravene for å være en funksjon: Hvert element X som tilhører domenet har et unikt bilde.

Derfor:

f (x) = y = log_til x , Med en> 0 og forskjellig fra 1.

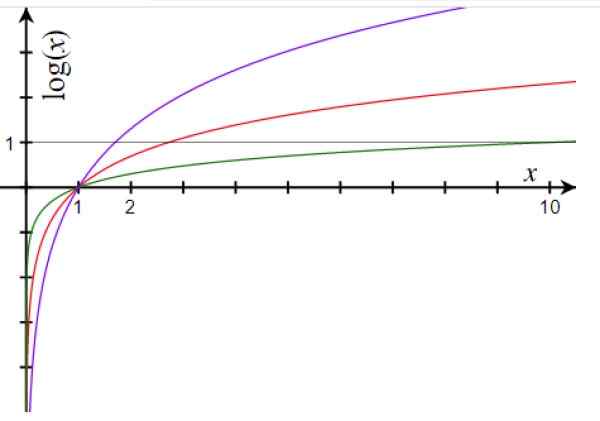
Figur 1. Logaritmefunksjonsgraf for base 10 (grønn), base E (rød) og base 1.7 (lilla). Kilde: Wikimedia Commons.

De viktigste egenskapene til logaritmisk funksjon er:

-Dens domene er all reais større enn 0, ikke inkludert 0. Det er med andre ord ingen logaritme eller negative tall på noen base. I form av et intervall:

Sol _F = (0, ∞+)

-Logaritmen til et tall kan være negativ, positiv eller 0, slik at dens rekkevidde eller rute er:

RGO _F = (-∞, ∞+)

-Logaritmisk funksjon vokser alltid for en> 1 og synker<1.

-Det inverse av f (x) = log_til x er den eksponentielle funksjonen.

Logaritmefunksjonen er faktisk basert på den omvendte funksjonen til den potensielle funksjonen:

F^-1(x) = a^og

Siden logaritmebasert til av et tall x, Det er tallet og som basen må heves til å få x.

-Baselogaritmen er alltid 1. Dermed grafen til f (x) = log_til x Kryss alltid til x -aksen på punktet (1.0)

-Den logaritmiske funksjonen er transcendent og kan ikke uttrykkes som polynom eller som en kvotient for disse. I tillegg til logaritme inkluderer denne gruppen trigonometriske og eksponentielle funksjoner, blant andre.

[TOC]

Eksempler

Den logaritmiske funksjonen kan etableres gjennom forskjellige baser, men de mest brukte er 10 og og, hvor og Det er antall Euler lik 2.71828 .. .

Når basen 10 brukes, kalles logaritmen desimal logaritme, vulgær logaritme, Briggs eller bare logaritme for å tørke.

Og hvis tallet E brukes, kalles det neperisk logaritme, av John Napier, den skotske matematikeren som oppdaget logaritmene.

Kan tjene deg: Multiplikativ omvendt: Forklaring, eksempler, løste øvelser

Notasjonen som brukes for hver er som følger:

-Desimal logaritme: log₁₀ x = log x

-Neperian logaritme: ln x

Når en annen base skal brukes, er det absolutt nødvendig. For eksempel, hvis det handler om logaritmer på base 2, er det skrevet:

y = log₂ x

La oss se på nummer 10 -logaritmen i tre forskjellige baser, for å illustrere dette poenget:

Logg 10 = 1

ln 10 = 2.30259

Logg₂ 10 = 3.32193

Vanlige kalkulatorer bringer bare desimale logaritmer (log) og neperisk logaritme (LN -funksjon). På internett er det kalkulatorer med andre baser. I alle fall kan leseren bekrefte, ved hjelp av det samme, at den med de tidligere verdiene er oppfylt:

10¹ = 10

og^2.3026 = 10.0001

2^3.32193 = 10.0000

Små desimalforskjeller skyldes mengden desimaler som er tatt i beregningen av logaritmen.

Fordelene med logaritmer

Blant fordelene ved å bruke logaritmene er den enkle de gir for å jobbe med stort antall, ved å bruke logaritmen sin i stedet for nummeret direkte.

Dette er mulig fordi logaritmefunksjonen vokser saktere ettersom tallene er større, som vi setter pris på i grafikken.

Så selv når det gjelder veldig stort antall, er logaritmene deres mye mindre, og manipulering av lite tall er alltid enklere.

I tillegg oppfyller logaritmene følgende egenskaper:

-Produkt: Logg (a.b) = log a + log b

-Kvotient: log (a/b) = log a - log b

-Makt: log a^b = b.Logg a

Og på denne måten blir produkter og kvotienter summer og subtraksjon av mindre antall, mens potensieringen blir omgjort til et enkelt produkt, selv om strømmen er høy.

Det er grunnen til skala.

Kan tjene deg: eksterne alternative vinkler: øvelser og øvelser løstFigur 2. Logaritmer brukes på Richter -skalaen for å kvantifisere størrelsen på jordskjelv. Bildet viser en bygning kollapset i Concepción, Chile, under jordskjelvet i 2010. Kilde: Wikimedia Commons.

La oss se på et eksempel på håndteringen av egenskapene til logaritmene:

Eksempel

Finn verdien av x i følgende uttrykk:

Logg (5x +1) = 1 + log (2x-1)

Svar

Vi har en logaritmisk ligning her, med tanke på det faktum at det ukjente er på logaritme -argumentet. Det løses ved å legge igjen en enkelt logaritme på hver side av likhet.

Vi begynner med å plassere alle vilkårene som inneholder "x" til venstre for likhet, og de som bare inneholder tall til høyre:

Logg (5x+1) - Logg (2x -1) = 1

Til venstre har vi subtraksjon av to logaritmer, som kan skrives som logaritmen til en kvotient:

Logg [(5x+1)/ (2x-1)] = 1

Til høyre er imidlertid nummer 1, som vi kan uttrykke som log 10, som vi så tidligere. Så:

Logg [(5x+1)/ (2x-1)] = log 10

For at likhet skal oppfylles, argumenter av logaritmene må være de samme:

(5x+1)/ (2x-1) = 10

5x + 1 = 10 (2x - 1)

5x + 1 = 20 x - 10

-15 x = -11

x = 11/15

Søknadsøvelse: Richter's Scale

I 1957 skjedde det et jordskjelv i Mexico hvis størrelse var 7.7 på Richter -skalaen. I 1960 skjedde det en annen jordskjelv med mest størrelse i Chile, 9.5.

Beregn hvor mange ganger var det chilenske jordskjelvet mer intenst enn Mexico, vel vitende om at størrelsen m_R På Richter -skalaen er den gitt av formelen:

M_R = log (10⁴ Yo)

Løsning

Størrelsen i Richter -skalaen til et jordskjelv er en logaritmisk funksjon. Vi skal beregne intensiteten til hvert jordskjelv, siden vi har Richter -størrelsene. La oss gjøre det trinn for trinn:

Kan tjene deg: primo -tall: egenskaper, eksempler, øvelser

-Mexico: 7.7 = Logg (10⁴ Yo)

Ettersom den omvendte av logaritmefunksjonen er eksponentiell, bruker vi dette på begge sider av likhet med den hensikt å rydde I, som finnes i logaritmens argument.

Siden de er desimale logaritmer, er basen 10. Så:

I løpet av høyre, 10 og log (10⁴ I) de blir kansellert (som med kvadratet og kvadratroten), og er: å forlate:

10 ^7.7 = 10⁴ Yo

Intensiteten til jordskjelvet i Mexico var:

Yo_M = 10 ^7.7 / 10⁴ = 10^3.7

 -Chili: 9.5 = Logg (10⁴ Yo)

Den samme prosedyren fører oss til intensiteten av det chilenske jordskjelvet i_Ch:

Yo_Ch = 10 ^9.5 / 10⁴ = 10^5.5

 Nå kan vi sammenligne begge intensitetene:

Yo_Ch / Yo_M = 10^5.5 / 10^3.7 = 10^1.8 = 63.1

 Yo_Ch = 63.1. Yo_M

Chiles jordskjelv var omtrent 63 ganger mer intenst enn Mexico. Ettersom størrelsen er logaritmisk, vokser den saktere enn intensitet, så en forskjell på 1 i størrelsesorden betyr en 10 ganger større amplitude av den seismiske bølgen.

Forskjellen mellom størrelsene på begge jordskjelvene er 1.8, derfor kunne vi forvente en forskjell i intensiteter nærmere 100 enn 10, som effektivt skjedde.

Faktisk, hvis forskjellen hadde vært 2 nøyaktig, ville det chilenske jordskjelvet vært 100 ganger mer intens enn meksikansk.

Referanser

1. Carena, m. 2019. Preuniversity Mathematics Manual. National University of the Coast.
2. Figuera, J. 2000. Matematikk 1. Diversifisert år. Co-bo-utgaver.
3. Jiménez, r. 2008. Algebra. Prentice Hall.
4. Larson, r. 2010. Beregning av en variabel. 9na. Utgave. McGraw Hill.
5. Stewart, J. 2006. Preccculment: Matematikk for beregning. 5. plass. Utgave. Cengage Learning.