Ekte ekte variabel funksjon og dens grafiske representasjon

EN ekte ekte variabel funksjon Ta et tall som tilhører settet med reelle tall og knytter det til en annen verdi, også reelt, gjennom en unik korrespondanseregel. Dette betyr at det reelle tallet oppnår gjennom denne regelen et unikt bilde.

Numeriske avgangsvariabler er vanligvis betegnet med bokstav X, mens bildet deres er bokstaven og. På den annen side, til korrespondanse -regelen som kobler dem, kalles også med en annen bokstav i alfabetet, for eksempel "F" -funksjonen, selv om en annen kan brukes.  I kompakt notasjon er det skrevet:

f: x → y = f (x)

Figur 1. Graf over en ekte polynomfunksjon

Til variabelen  x det kalles uavhengig variabel, mens og Det er den avhengig variabel. Funksjonen kan uttrykkes på flere måter, for eksempel gjennom en matematisk uttalelse som disse:

• f (x) = 2x −3
• H (x) = −3x²
• 

En annen uttrykksform er gjennom en graf, noe som er veldig nyttig fordi den lar deg sette pris på oppførselen til funksjonen til et enkelt blikk. Å bygge en graf er veldig enkelt ved hjelp av et kartesisk koordinatsystem, der jevnaldrende [x, f (x)] er representert som punkter i flyet. Så blir de sammen med en myk og kontinuerlig linje, kan du se hvordan funksjonen er.

Eksempler

For å bygge grafen kan du ty til en tabell med verdier der punktene til grafen er plassert. For variable X -verdier er valgt som hører til funksjonen til funksjonen, det vil si de som når de erstattes i formelen, i sin tur viser reelle tall.

Når verdiene til x er valgt, bestemmes bildet Y = f (x), og på denne måten oppnås punktene par [x, f (x)] som vil være grafisk.

Kan tjene deg: Homografisk funksjon: Hvordan graf, løste øvelser

Det er noen punkter som er viktige og bør inkluderes i tabellen: de der grafen kutter til koordinataksene, at hvis de eksisterer, fordi ikke alle funksjoner krysser dem.

For å beregne dem, fortsett som følger:

-Kryss med aksen og: x = 0 er laget i funksjonsformelen og den tilsvarende verdien beregnes.

-Kryss med x -aksen: Y = 0 er ferdig og ligningen f (x) = 0 er løst.

Deretter trekkes det kartesiske koordinatsystemet og hvert av punktene plottes, som deretter blir sammen med en myk og kontinuerlig linje om mulig.

Eksempel 1

Bygg en tabell med verdier og grafen for følgende funksjon:

f (x) = x² −4

Før du starter må du finne domenet til funksjonen, som er settet med reelle verdier som funksjonen eksisterer. Siden det er en kvadratisk funksjon, har enhver x -verdi som tilhører de virkelige tallene et ekte bilde, i henhold til F (x).

Deretter kan tabellen bygges ved å velge hvilken som helst x -verdi, og det enkleste er å starte med kryssene mellom grafen med aksene, hvis det er. Etter å ha funnet dem, blir andre punkter søkt å fullføre tabellen.

For x = 0

f (0) = -4

Derfor er det første punktet i tabellen (0, -4). Dette er skjæringspunktet mellom grafen med aksen og.

For y = 0

Da blir y = 0 utført og ligningen som resultatene blir løst:

x² −4 = 0

x² = 4

Løsningene av denne ligningen er: x₁= 2 og x₂= -2. Derfor er det to kryss med X -aksen, som er punktene: (−2.0) og (2.0).

Kan tjene deg: perfekte tall: hvordan identifisere dem og eksempler

Nå kan du finne flere poeng å legge til verdens tabell:

For x = 1

f (1) = (1)² - 4 = −3

For x = - 1

f (−1) = (−1)² - 4 = −3

For x =  3

f (3) = (3)² - 4 = 5

For x =  -3

f (−3) = (−3)² - 4 = 5

Verditabell

Følgende tabell viser punktene som er oppnådd, som vil tjene til å bygge grafen til F (x):

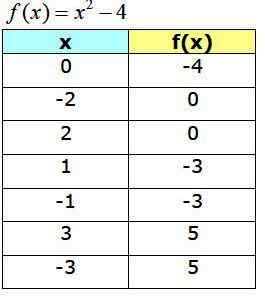Funksjonsgraf f (x) = x² −4

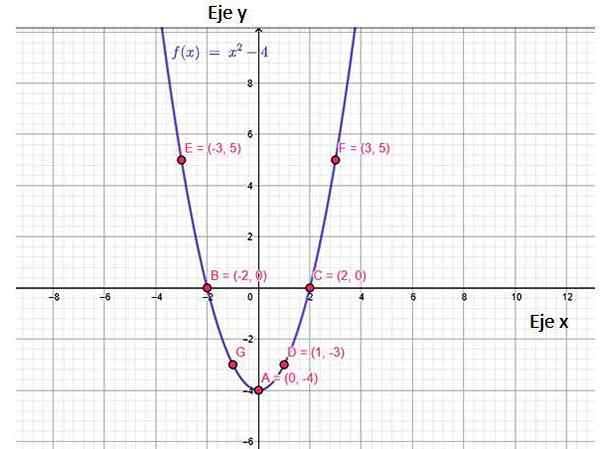Figur 2. Funksjon F (x) Funksjonsgraf, som viser noen punkter som tilhører den, inkludert kryss med akser. Kilde: f. Zapata, gjennom Geogebra.

Grafen til denne funksjonen er en lignelse, som åpnes og har på et minimumspunkt, kalt toppunkt, av koordinater (0, −4). Det er interessant å merke seg at verdiene til f (x) begynner ved y = -4 til ∞. Dette er utvalget av funksjonen.

Av grafen kan det konkluderes med at funksjonen er kontinuerlig, avtar i intervallet (−∞, 0) og øker derfra.

Eksempel 2

Å ha diagrammet over funksjonen er det mulig å kjenne dets domene, rekkevidden, kryssene det har med aksene og visualisere dens generelle oppførsel (vekst og reduksjon).

Nedenfor er grafen til polynomfunksjonen:

f (x) = - x⁴+4x²+1

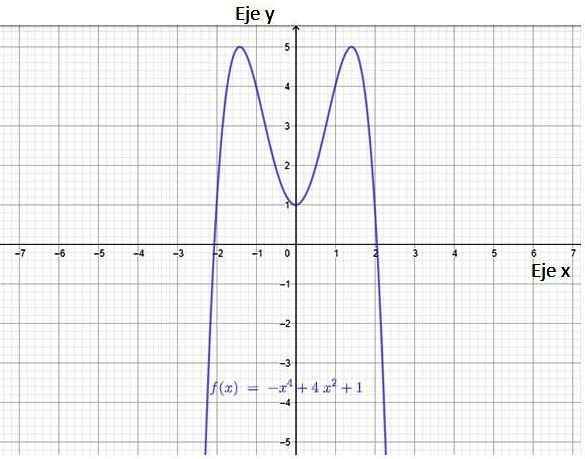Figur 3. Graf over en polynomfunksjon. Kilde: f. Zapata gjennom Geogebra.

Fra bildet følger det at funksjonen har to kryss med X-aksen, punktene (-2.0) og (2.0). Den har også et kryss med Y -aksen, punktet (0,1).

Domenet til en polynomfunksjon er det komplette settet med reelle tall, det blir også advart om at funksjonen er kontinuerlig og har symmetri rundt den vertikale aksen. Det kan faktisk verifiseres at denne funksjonen er Symmetri for. En funksjon er selv om den møtes:

Kan tjene deg: Grønn teorem, demonstrasjon, applikasjoner og øvelser

f (x) = f (-x)

Leseren kan bekrefte at ved å erstatte -x i funksjonen, endres den ikke.

Det er to interessante punkter, som er på høyden av y = 5, er maksimale verdier for funksjonen. Området for denne funksjonen, det vil si settet med verdier som variabelen tar og strekker seg fra -∞ til y = 5 nøyaktig.

For å kjenne verdiene til x hvis bilde er y = 5, erstattes denne verdien i funksjonen:

5 = - x⁴+4x²+1

Og denne ligningen oppnås:

- x⁴ + 4x² - 4 = 0

Hvis løsninger er −√2 og + √2. Vel, funksjonen er:

-Vokser Fra x -∞ til x = −√2

-Minkende Fra x = −√2 til x = 0

-Vokser Fra x = 0 til x = + √2

-Minkende Fra x = + √2 og utover.

Trening løst

Bygg grafen for følgende funksjon:

f (x) = √ (x-5)

Løsning

Først må du bestemme domenet til funksjonen, for å vite hvilke verdier av x som kan velges for å bygge tabellen. Når det gjelder den foreslåtte funksjonen, må mengden i roten alltid være positiv eller lik 0, derfor:

x - 5 ≥ 0

x ≥ 5

Derfor kan bare verdier større enn eller lik 5 velges for tabellen. Når det gjelder kryss med koordinataksene, er den eneste muligheten å gjøre y = 0, og deretter x = 5.

Det er ubrukelig å gjøre x = 0 for denne funksjonen, da denne verdien ikke tilhører domenet.

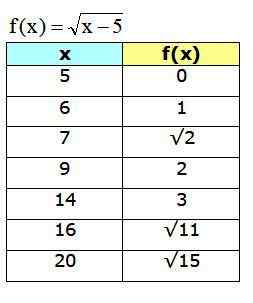
Grafen som er oppnådd er:

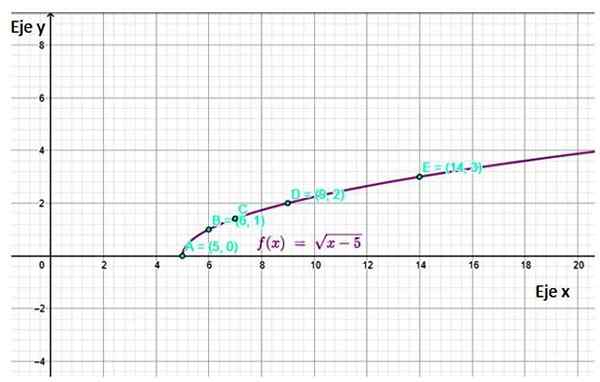Figur 4. Funksjonsgraf f (x) som viser noen av punktene beregnet i tabellen. Kilde: f. Zapata gjennom Geogebra.

Referanser

1. E-Math Zone. Typer funksjoner. Gjenopprettet fra: Emathzone.com.
2. Hoffman, J.G. Valg av matematikkproblemer. Ed. Spphinx.
3. Matematikk er morsomt. Commons fungerer referanse. Gjenopprettet fra: Mathisfun.com.
4. Requena, b. Universformler. Typer funksjoner. Gjenopprettet fra: Universoformulas.com.
5. Stewart, J. 2006. Preccculment: Matematikk for beregning. 5. plass. Utgave. Cengage Learning.