Gradfunksjoner større enn to (eksempler)

En (polynom) av karakter større enn to har den generelle formen:

f (x) = a₀ + til₁x +a₂x² +.. .til_nxⁿ

Med n = 3, 4, 5, ... et ikke -negativt heltall og koeffisientene til_enten, til₁… til_n, som vanligvis er reelle tall.

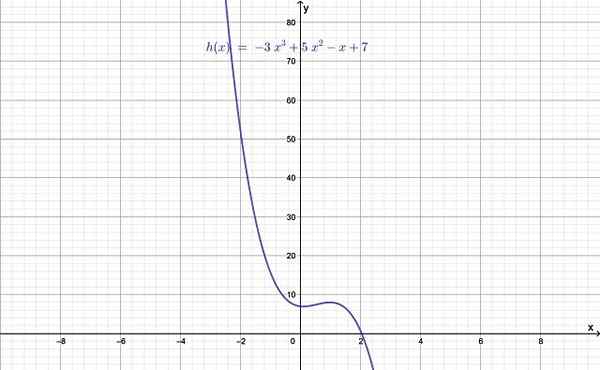Figur 1.- Graf over en gradfunksjon større enn 2. Kilde: f. Zapata.

Graden av funksjonen er gitt av verdien av n, den største av eksponentene og som igjen er større enn 2. Når n = 0 er en konstant funksjon, hvis n = 1 er det en lineær funksjon, og til slutt med n = 2 er det en kvadratisk funksjon.

Eksempler på funksjoner på større enn to, i variabelen "x", er følgende:

• f (x) = x³
• H (x) = - 3x³ + 5x² - X + 7
• g (x) = x⁴ - 6x² + 25

Funksjonen f (x) = x³ Det er den enkleste av alle funksjoner på større enn to, og dens grad er 3. En grad 3 er også kjent som kubisk funksjon. For sin del er G (x) grad 4, for å være 4 den maksimale eksponenten.

Verdien av n er veldig viktig fordi den bestemmer den generelle formen for grafen, og også den maksimale mengden røtter eller kryss som funksjonen har med den horisontale aksen. Faktisk vil en 3 -grade -funksjon berøre den horisontale aksen på det meste 3 poeng, en av klasse 4 vil gjøre det på det meste på 4 poeng og så videre.

Når det gjelder det uavhengige begrepet, indikerer det i en polynomfunksjon i noen grad skjæringspunktet mellom funksjonen med den vertikale aksen.

Kjennetegn på polynomfunksjonene til større enn to

Domene

Domenet til en funksjon er settet med verdier som tillater beregning av verdiene til y = f (x). For polynomfunksjoner er dette settet det av reelle n tall, eller settet med komplekse tall, om nødvendig for å utvide domenet.

Kan tjene deg: Trigonometriske grenser: Hvordan løse dem, løste øvelser

Betyr at gitt polynomfunksjonen f (x) = a₀ + til₁x +a₂x² +.. .til_nxⁿ, Du kan alltid erstatte et hvilket.

Område

Det er settet som er dannet av alle verdiene som er anskaffet f (x), det vil si bildene som hver verdi av x har gjennom funksjonen f (x). For polynomfunksjoner større enn 2, er dette settet av reelle tall.

Røtter til funksjonen

Er verdiene til x som det er oppfylt for at f (x) = 0. Som antydet ovenfor, indikerer graden av funksjonen det maksimale antall røtter som den kan ha, selv om ikke alle av dem nødvendigvis er reelle.

Når funksjonens koeffisienter er reelle tall, tilsvarer de virkelige røttene kryssene mellom funksjonen med x -aksen.

Eksempel 1

De rasjonelle røttene til funksjonen f (x) = 2x³ - 9x² + 7x + 6 finner du gjennom følgende teorem:

Hvis roten til f (x) = a₀ + til₁x +a₂x² +.. .til_nxⁿ Det er B/C -formen, så de mulige verdiene for B er faktorer for en_enten og de mulige verdiene for C er faktorer for en_n.

For eksemplets funksjon er de allerede forenklede kombinasjonene: ± 6, ± 3, ± 2, ± 1, ± 3/2, ± ½. Nå blir hver enkelt testet gjennom prosedyren for syntetisk avdeling, for eksempel. Når divisjonsresten er 0, er den påviste verdien en rot:

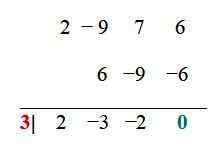
Verdien x₁ = 3 er en rot eller null av funksjonen, derfor (x - 3) er en vanlig faktor av f (x), og dette kan skrives som:

Det kan tjene deg: Unitary Circle: Trigonometric Functions and Applications

f (x) = (x - 3) ∙ (2x² −3x −2)

De resterende to røttene er verdiene som tilfredsstiller 2x -ligningen² −3x −2 = 0. Denne ligningen kan løses gjennom den generelle formelen, en vitenskapelig kalkulator eller gjenta den forrige Tanteo -prosessen.

Disse røttene er x₂ = 2 og x₃ = - ½, og nå kan f (x) skrives som et produkt av tre faktorer:

f (x) = (x - 3) ∙ (x - 2) ⋅ (x + ½)

Kryssene mellom f (x) med x -aksen er punktene: P₁ (3.0), P₂(2.0) og P₃(−½, 0). Grafen til funksjonen, oppnådd med Geogebra, viser kryssene med X -aksen:

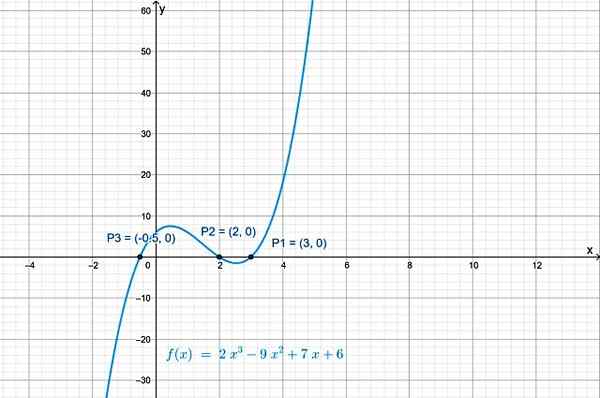Figur 2.- En polynomfunksjon i grad 3 har tre kryss med den horisontale aksen. Kilde: f. Zapata.

Kryss med den vertikale aksen

For å finne skjæringspunktet mellom funksjonen med den vertikale aksen må du finne F (0), som ganske enkelt er til₀.

Eksempel 2

Finn krysset mellom f (x) = 2x³ - 9x² + 7x + 6 Med den vertikale aksen er det veldig enkelt, når du lager x = 0 i f (x) oppnås det:

f (x) = 6

Og kryssingspunktet for funksjonen med den vertikale aksen er P₄(0,6).

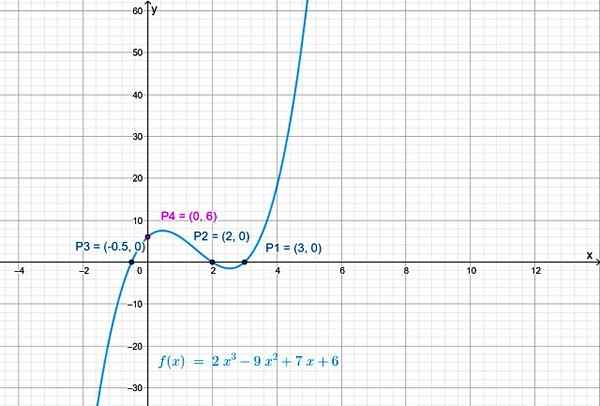Figur 3. Skjæringspunktet mellom kurven med den vertikale aksen lager x = 0 i F (x). Kilde: f. Zapata.

Kontinuitet

Polynomiske funksjoner generelt, og spesielt de med høyere enn 2 er kontinuerlige funksjoner i hele sitt domene, betyr dette at de ikke har noen hopp, trinn, hull eller verdier som de ikke er definert. De har heller ikke asymptoter, som er vertikale, horisontale eller skrå rett som funksjonen nærmer seg uten å krysse dem.

Disse egenskapene til mykhet og kontinuitet blir verdsatt i grafene vist ovenfor.

Graf over funksjonene til høyere enn 2

Grafene over funksjonene til høyere enn 2 er kontinuerlige og myke, og deres form avhenger av graden av polynomet.

Kan tjene deg: Permutasjoner uten repetisjon: Formler, demonstrasjon, øvelser, eksempler

For eksempel, de av grad 3 -ram, har det et negativt tegn på begrepet med høyeste grad).

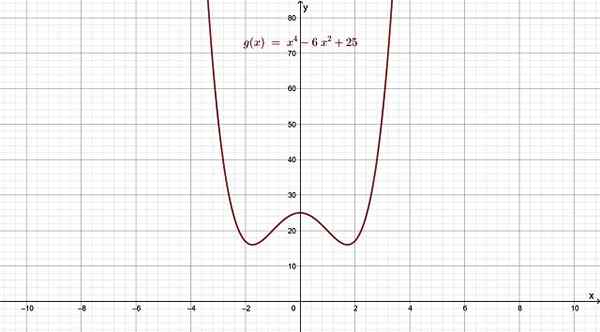Figur 4. Polyinomisk funksjon av klasse 4, hvis graf ligner en bokstav w. Kilde: f. Zapata.

For verdier av x vekk fra x = 0, både venstre og høyre, oppfører funksjonen hvordan begrepet størst grad ville gjort, fordi dette råder over andre når x blir veldig stor eller veldig liten.

I bildet som følger, blir funksjonen f (x) = 2x sammenlignet³ - 9x² + 7x + 6 med funksjonen r (x) = x³ Og det blir satt pris på at formen på begge kurver ligner på verdier av x som er langt fra x = 0.

For store x -verdier vokser funksjonen raskt ved å pleie +∞, mens for negative x -verdier avtar funksjonen raskt og har en tendens til −∞.

Figur 5.- Alle funksjoner N -funksjoner oppfører seg på samme måte når de beveger seg bort fra x = 0, både venstre og høyre. Kilde: f. Zapata.

Sammenligning av dreiemomentkurver (figur 4) med den rare graden (figur 2), så lenge koeffisienten som følger med den høyeste karakteren har samme tegn, observeres det at de rare gradskurvene begynner fra "y" negativ og negativ og vokse, mens målklassen begynner i "y" positivt og reduseres.

Referanser

1. Barnett, r. 2000. Precculment: Funksjoner og grafikk. 4. plass. Utgave. McGraw Hill.
2. Beregning.DC. Polynomiske funksjoner. Gjenopprettet fra: Beregning.DC.
3. Larson, r. 2012. Forkalkning. 8. Utgave. Cengage Learning.
4. Stewart, J. 2007. Preccculment: Matematikk for beregning. 5. plass. Utgave. Cengage Learning.
5. Varsity Tutorrs. Grafering av polynomfunksjoner. Hentet fra: Warsitytorm.com.