Grad av et polynom hvordan det bestemmes, eksempler og øvelser

Han grad av et polynom i en variabel er gitt av begrepet som den viktigste eksponenten har, og hvis polynomet har To eller flere variabler, Da bestemmes graden av summen av eksponentene for hvert semester, den viktigste summen av det polynomiale vesenet.

La oss se hvordan vi kan bestemme graden av polynom på en praktisk måte.

Figur 1. Den berømte Einstein -ligningen for energi E er en absolutt monomial grad 1 for massevariabelen, betegnet med M, siden lysets hastighet blir ansett som konstant. Kilde: Piqssels.

Anta at polynomet P (x) = -5x + 8x³ + 7 - 4x². Dette polynomet er av en variabel, i dette tilfellet er det variabelen x. Dette polynomet består av flere begreper, som er følgende:

-5x; 8x³; 7; - 4x²

 La oss velge mellom de fire begrepene hvis eksponent er større, dette begrepet er:

8x³

Og nå hva er eksponenten? Svaret er 3. Derfor er P (x) et polynom i grad 3.

Hvis det aktuelle polynomet har mer enn en variabel, kan graden være:

-Absolutt

-I forhold til en variabel

Den absolutte graden blir forklart i begynnelsen: å legge til eksponentene for hvert begrep og velge den største.

På den annen side er graden av polynom med hensyn til en av variablene eller bokstavene, den største verdien av eksponenten som har sagt brev. Poenget vil være tydeligere med eksemplene og øvelsene løst fra følgende seksjoner.

[TOC]

Eksempler på karakter av et polynom

Polynomer kan klassifiseres etter graden, å kunne være i første grad, andre klasse, tredje klasse og så videre. For eksempel på figur 1 er energi en monomiell for masse for masse.

Kan tjene deg: kongruens: kongruente figurer, kriterier, eksempler, øvelser

Det er også viktig å observere at antallet begrep som et polynom har er lik graden pluss 1. Så:

-Første grads polynomer har 2 termer: a₁x + a_enten

-Det andre -graders polynomet har 3 begreper: a₂x² + til₁x + a_enten

-En tredje grads polynom har 4 termer: a₃x³ + til₂x² + til₁x + a_enten

Og så videre. Den imøtekommende leseren vil ha observert at polynomene til de tidligere eksemplene er skrevet på en synkende måte, det vil si først å plassere begrepet med hovedgraden.

Ulike polynomer vises i følgende tabell, både fra en og flere variabler og deres respektive absolutte grader:

Tabell 1. Eksempler på polynomer og deres grader

Polynom	Grad
3x4+5x3-2x+3	4
7x3-2x2+3x-6	3
6	0
X-1	1
x5-bx4+Abx3+AB3x2	6
3x3og5 + 5x2og4 - 7xy2 + 6	8

De to siste polynomene har mer enn en variabel. Begrepet som har den største absolutte graden har stått ut med fet skrift, slik at leseren raskt sjekker graden. Viktig å huske at når variabelen ikke har noen skriftlig eksponent, forstås det at exponenten er lik 1.

For eksempel i det fremtredende begrepet AB³x² Det er tre variabler, nemlig: til, b og x. I det begrepet, til Den er forhøyet til 1, det vil si:

a = a¹

Derfor AB³x² = a¹b³x²

Siden eksponenten for B er 3 og den for X er 2, følges det umiddelbart at graden av dette begrepet er:

1+3+2 = 6

Og det er den absolutte graden av polynom, siden ingen andre av begrepene har større grad.

Prosedyre for å jobbe med polynomer

Når du jobber med polynomer er det viktig å ta hensyn til graden av det samme, siden det i utgangspunktet og før du utfører noen operasjon, er det praktisk å følge disse trinnene, som graden gir veldig viktig informasjon:

-Bestill preferansen polynom i avtagende forstand. På denne måten er begrepet med høyeste karakter til venstre og den med den laveste til høyre.

Kan tjene deg: Endecagon

-Reduser lignende vilkår, en prosedyre som består i å legge til alle vilkårene for lik variabel og grad som er i uttrykket algebraisk.

-Om nødvendig er polynomene fullført, og ispisservilkår hvis koeffisient er 0, i tilfelle vilkår med en viss eksponent.

Bestill, reduser og fullfør et polynom

Gitt polynomet P (x) = 6x² - 5x⁴- 2x+3x+7+2x⁵  - 3x³ + x⁷ -12 Det blir bedt om å bestille det avtagende, redusere de lignende vilkårene hvis det er og fullføre vilkårene som mangler fra å være nøyaktige.

Den første tingen å se etter er begrepet med den viktigste eksponenten, som er graden av polynom, som viser seg å være:

x⁷

Derfor er P (x) grad 7. Da bestilles polynomet, og starter med dette begrepet til venstre:

P (x) = x⁷ + 2x⁵ - 5x⁴ - 3x³ + 6x² - 2x+3x+7 -12

De lignende begrepene er nå redusert, som er følgende: - 2x og 3x på den ene siden. Og 7 og -12 på den andre. For å redusere dem blir koeffisientene tilsatt algebraisk og variabelen blir uendret (hvis variabelen ikke vises ved siden av koeffisienten, må det huskes at x⁰ = 1):

-2x+3x = x

7 -12 = -5

Disse resultatene erstattes i P (x):

P (x) = x⁷ +2x⁵ - 5x⁴ - 3x³ + 6x² + x -5

Og til slutt blir polynomet undersøkt for å se om en eksponent mangler og faktisk, et begrep hvis eksponent er 6 mangler, derfor er den fullført med nuller som dette:

P (x) = x⁷ + 0x⁶ +2x⁵ - 5x⁴ - 3x³ + 6x² + X - 5

Nå observeres det at polynomet satt igjen med 8 vilkår, siden som sagt før, antall begreper er lik grad + 1.

Viktigheten av graden av et polynom i summen og subtraksjonen

Med polynomer kan sum og subtraksjonsoperasjoner utføres, der bare lignende vilkår legges til eller trekkes fra, som er samme variabel og samme grad. Hvis det ikke er noen lignende vilkår, blir summen eller subtraksjonen igjen bare angitt.

Kan tjene deg: Distributive eiendommer

Når summen eller subtraksjonen er gjort, er sistnevnte summen av det motsatte, graden av det resulterende polynomet alltid er lik eller mindre enn graden av polynomet tilsetning av større grad.

Løste øvelser

- Trening løst 1

Finn følgende sum og bestem dens absolutte grad:

til³- 8ax²  + x³ + 5. plass²X - 6ax² - x³ + 3³ - 5. plass²x - x³ + til³+ 14AX² - x³

Løsning

Det er et polynom av to variabler, så det er praktisk å redusere de lignende vilkårene:

til³- 8ax²  + x³ + 5. plass²X - 6ax² - x³ + 3³ - 5. plass²x - x³ + til³+ 14AX² - x³ =

= a³ + 3³ + til³ - 8ax² - 6ax²+ 14AX² +5. plass²X - 5a²x+ x³- x³- x³- x³ =

= 5a³ - 2x³

Begge begrepene er grad 3 i hver variabel. Derfor er den absolutte graden av polynom 3.

- Trening løst 2

Uttrykke som polynom området for følgende flate geometriske figur (figur 2 til venstre). Hva er den resulterende grad av polynom?

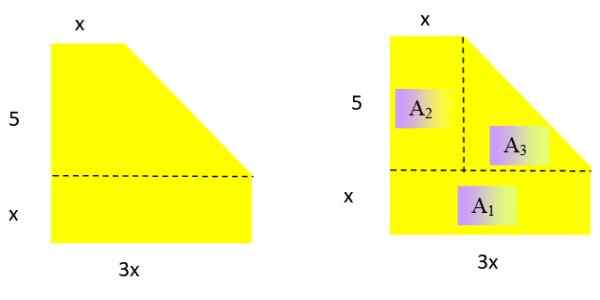Figur 2. På venstre side løste figuren for året 2 og til høyre, den samme figuren som er dekomponert i tre områder hvis uttrykk er kjent. Kilde: f. Zapata.

Løsning

Å være et område, må det resulterende polynomet være grad 2 i variabel x. For å bestemme et tilstrekkelig uttrykk for området, blir figuren brutt ned i kjente områder:

Området til et rektangel og en trekant er henholdsvis: Base x høyde og Base x høyde /2

TIL₁ = x . 3x = 3x²; TIL₂ = 5 . x = 5x; TIL₃ = 5 . (2x /2) = 5x

Merk: Basen til trekanten er 3x - x = 2x og høyden er 5.

Nå blir de tre utførte uttrykkene lagt til, med dette har du området av figuren avhengig av x:

3x² + 5x + 5x = 3x² + 10x

Referanser

1. Baldor, a. 1974. Elementær algebra. Venezuelanske kulturelle s.TIL.
2. Jiménez, r. 2008. Algebra. Prentice Hall.
3. Wikilibros. Polynomer. Gjenopprettet fra: er. Wikibooks.org.
4. Wikipedia. Karakter (polynom). Gjenopprettet fra: er.Wikipedia.org.
5. Zill, d. 1984. Algebra og trigonometri. Mac Graw Hill.