Frihetsgrader hvordan du beregner dem, typer, eksempler

De grader av frihet I statistikk er antall uavhengige komponenter i en tilfeldig vektor. Hvis vektoren har n komponenter og det er p lineære ligninger som relaterer dens komponenter, deretter grad av frihet Det er n-p.

Konseptet av grader av frihet Det vises også i teoretisk mekanikk, hvor de i en brutto modus tilsvarer dimensjonen av rommet der partikkelen beveger seg, bortsett fra antall ligaturer.

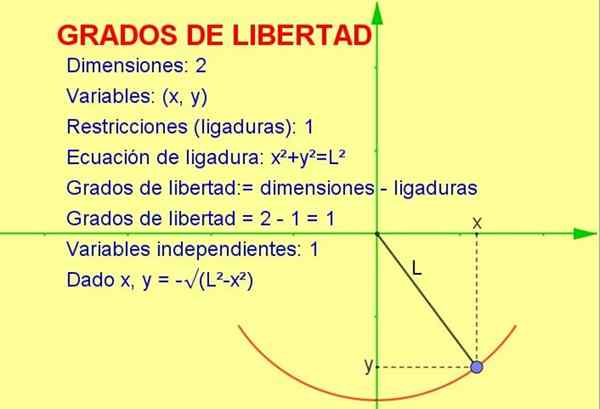
Figur 1. En pendel beveger seg i to dimensjoner, men den har bare en grad av frihet fordi den er forpliktet til å bevege seg i en radiusbue l. Kilde: f. Zapata.

Denne artikkelen vil diskutere begrepet frihetsgrader som er brukt på statistikk, men et mekanisk eksempel er lettere å visualisere på en geometrisk måte.

[TOC]

Typer frihetsgrader

I henhold til konteksten det brukes, kan måten å beregne antall frihetsgrader variere, men den underliggende ideen er alltid den samme: totale dimensjoner mindre antall begrensninger.

I et mekanisk tilfelle

Tenk på en partikkel som svinger bundet til et tau (en pendel) som beveger seg i det vertikale planet X-Y (2 dimensjoner). Imidlertid er partikkelen forpliktet til å bevege seg på radiusomkretsen lik tauets lengde.

Ettersom partikkelen bare kan bevege seg på den kurven, antallet antall grader av frihet Det er 1. Dette kan visualiseres i figur 1.

Måten å beregne antall frihetsgrader er å utgjøre forskjellen i antall dimensjoner bortsett fra antall begrensninger:

Frihetsgrader: = 2 (dimensjoner) - 1 (ligering) = 1

En annen forklaring som lar oss nå resultatet er som følger:

-Vi vet at den to -dimensjonale posisjonen er representert med et koordinatpunkt (x, y).

-Men ettersom poenget må oppfylle omkretsligningen (x² + og² = L²) For en gitt verdi av variabel x, bestemmes variabelen og bestemmes av nevnte ligning eller begrensning.

På denne måten er bare en av variablene uavhengig og systemet har En (1) frihetsgrad.

Kan tjene deg: Klassisk sannsynlighet: Beregning, eksempler, løste øvelser

I et sett med tilfeldige verdier

Å illustrere hva konseptet betyr å anta vektoren

x = (x₁, x₂,..., x_n)

Representerer prøven av n Tilfeldige verdier normalt distribuert. I dette tilfellet den tilfeldige vektoren x har n uavhengige komponenter og derfor sies det at x har n grader av frihet.

La oss bygge vektoren nå r av avfallet

r = (x₁ - , x₂ - ,.. ., x_n - )

Der det representerer gjennomsnittet av prøven, som beregnes som følger:

= (x₁ + x₂ +.. .+ x_n) / n

Så summen

(x₁ - )+(x₂ - )+.. .+(x_n - ) = (x₁ + x₂ +.. .+ x_n) - n = 0

Det er en ligning som representerer en begrensning (eller ligering) i vektorelementene r av avfallet, siden hvis n-1 er kjent, vektorkomponenter r, Begrensningsligningen bestemmer den ukjente komponenten.

Derfor vektoren r av dimensjon n med begrensningen:

∑ (x_Yo - ) = 0

Har (N - 1) Frihetsgrader.

Igjen brukes det at beregningen av antall frihetsgrader er:

Frihetsgrader: = n (dimensjoner) - 1 (begrensninger) = n -1

Eksempler

Varians og frihetsgrader

Variansen s² Det er definert som gjennomsnittet av kvadratet for avvikene (eller avfallet) til dataprøven:

s² = (r•r) / (N-1)

hvor r er avfallsvektoren r = (x1 -, x2 -, .. ., Xn -) og det tykke punktet (•) er den skalære produktoperatøren. Alternativt kan variansformelen skrives som følger:

s² = ∑ (x_Yo - )² / (N-1)

I alle fall skal det bemerkes at når du beregner gjennomsnittet av avfallet, er det delt med (n-1) og ikke mellom n, siden som omtalt i forrige seksjon, antallet frihetsgrader vektor r er (n-1).

Hvis den for beregningen av variansen ble delt mellom n I stedet for (n-1), ville resultatet ha en skjevhet som er veldig viktig for verdier av n Mindre enn 50.

Det kan tjene deg: analytisk geometri

I litteratur vises også formelen for variansen med divisoren n i stedet for (n-1), når det gjelder varians av en befolkning.

Men settet med den tilfeldige variabelen av avfallet, representert av vektoren r, Mens den har dimensjon n, har den bare (n-1) frihetsgrader. Imidlertid, hvis datatummeret er stort nok (n> 500), konverger begge formlene til samme resultat.

Kalkulatorene og regnearkene tilbyr de to versjonene av variansen og standardavviket (som er kvadratroten til variansen).

Vår anbefaling, med tanke på analysen som presenteres her, er å alltid velge versjonen med (n-1) hver gang det er nødvendig å beregne variansen eller standardavviket, for å unngå resultater med skjevhet.

I Chi Square -distribusjonen

Noen sannsynlighetsfordelinger i kontinuerlig tilfeldig variabel avhenger av en parameter som heter grad av frihet, Dette er tilfellet med Chi Square -distribusjonen (χ²).

Navnet på nevnte parameter kommer bare fra grader av frihet til den tilfeldige vektoren som ligger til grunn for denne distribusjonen blir brukt.

Anta at det er G -populasjoner, hvorav N -størrelsesprøver tas:

X₁ = (x1₁, x1₂,... x1_n)

X2 = (x2₁, x2₂,... x2_n)

.. .

X_J = (xj₁, xj₂,… Xj_n)

.. .

Xg = (xg₁, Xg₂,… Xg_n)

En befolkning J som har gjennomsnittlig og standardavvik SJ, Følg normalfordelingen N (, SJ ).

Den karakteriserte eller normaliserte variabelen ZJ_Yo er definert som:

ZJ_Yo = (xj_Yo - ) / SJ.

Og vektoren ZJ Det er definert slik:

ZJ = (ZJ₁, ZJ₂,..., ZJ_Yo,..., ZJ_n) Og følg normalfordelingen karakterisert n (0.1).

Deretter variabelen:

Q = ((Z1₁ ^2 + Z2₁^2+.. . + Zg₁^2), .. ., (Z1_n^2 + Z2_n^2+.. . + Zg_n^2))

Følg distribusjonen χ²(g) kalte Chi Square distribusjon med frihetsgrad g.

I hypotesekontrasten (med et løst eksempel)

Når du vil lage en hypotesekontrast basert på et visst sett med tilfeldige data, er det nødvendig å vite antall frihetsgrader g For å kunne bruke Chi Square -testen.

Kan tjene deg: kontinuerlig ensartet distribusjon: egenskaper, eksempler, applikasjoner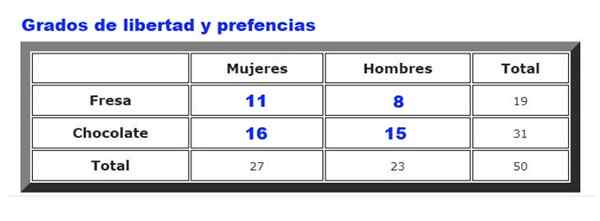 Figur 2. Er det et forhold mellom iskremsmak og kundens kjønn? Kilde: f. Zapata.

Som et eksempel vil dataene som samles inn om sjokolade eller jordbærispreferanser mellom menn og kvinner i en eller med isbutikk bli analysert. Frekvensen som menn og kvinner velger jordbær eller sjokolade, er oppsummert i figur 2.

Først beregnes den forventede frekvensbordet, som er laget ved å multiplisere Totalt rader for han Totalt kolonner, delt med Total data. Resultatet vises i følgende figur:

Figur 3. Beregning av forventede frekvenser basert på de observerte frekvensene (blå verdier i figur 2). Kilde: f. Zapata.

Deretter fortsetter vi med å beregne chi -plassen (fra dataene) etter følgende formel:

χ² = ∑ (f_enten - F_og)² / F_og

Hvor f_enten er de observerte frekvensene (figur 2) og f_og er de forventede frekvensene (figur 3). Summen er over alle rekker og kolonner, som i vårt eksempel gir fire vilkår.

Etter å ha utført operasjonene du får:

χ² = 0.2043.

Det er nå nødvendig å sammenligne med det teoretiske torget, som avhenger av antall frihetsgrader g.

I vårt tilfelle bestemmes dette tallet som følger:

G = (#filas - 1) (#columnas - 1) = (2 - 1) (2 - 1) = 1 * 1 = 1.

Det viser seg at antallet frihetsgrader G for dette eksemplet er 1.

Hvis du vil bekrefte eller avvise nullhypotesen (H0: det er ingen sammenheng mellom smak og kjønn) med et nivå av betydning på 1%, beregnes det teoretiske chi -plassen med frihetsgraden G = 1.

Verdien som gjør at den akkumulerte frekvensen blir søkt (1 - 0.01) = 0.99, det er 99%. Denne verdien (som kan fås fra tabellene) er 6.636.

Når den teoretiske chi overgår de beregnede, blir nullhypotesen bekreftet.

Det vil si at med dataene som er samlet inn, er det ingen sammenheng mellom variablene smak og kjønn.

Referanser

1. Minitab. Hva er frihetsgrader? Hentet fra: støtte.Minitab.com.
2. Moore, David. (2009) Grunnleggende anvendt statistikk. Antoni Bosch Editor.
3. Leigh, Jennifer. Hvordan beregne frihetsgrader i statistiske modeller. Gjenopprettet fra: Geniolandia.com
4. Wikipedia. Grad av frihet (statistikk). Gjenopprettet fra: er.Wikipedia.com
5. Wikipedia. Grad av frihet (fysisk). Gjenopprettet fra: er.Wikipedia.com