Historien om bakgrunns- og utviklingsgeometri fra opprinnelsen

De Geometrihistorie Det begynner med de første sivilisasjonene som benyttet seg av denne grenen av matematikk på en praktisk måte, nærmere bestemt folket i Indo -dalen og Babylon som kjente de stumpe trekantene, rundt 3000 til.C.

I skriftene til den egyptiske skribenten Ahmes (1550 til.C.) Metoder brukes til å beregne området til en sirkel. For deres del hadde babylonerne generelle regler for å måle volum og områder. 

Ahme Papyrus eller Rhind Mathematical Papyrus

Både sivilisasjoner, egypterne og babylonikerne, kjente versjoner av Pythagoras teorem 1500 år før Pythagorean -versjonene. På den annen side indianerne i den vediske perioden (1500-100 til.C.) brukte geometri i alterkonstruksjon.

[TOC]

Antikkens Hellas

Grekerne var tilbøyelige til utvikling av matematikk i lang tid. Karakterer som Pythagoras og Platon, relatert til tall med alt som finnes i verden. For dem var matematikk nøkkelen til å tolke universet; Dette idealet fulgte i tilhengerne av Pythagoreans i flere århundrer.

Tales of Miletus

Tales de Mileto var en av de første grekerne som bidro til fremskritt av geometri. Lenge brukt i Egypt og fra disse lærte grunnleggende kunnskapene. Han var den første som etablerte geometri måleformler.

Tales of Miletus

Han klarte å måle høyden på pyramidene i Egypt, og målte skyggen i det nøyaktige øyeblikket hvor høyden var lik målet på skyggen.

Pythagoras

Pythagoras

Innenfor det viktigste bidraget fra Pythagoras (569 til.C. - 475 a.C.) Til geometrien er det berømte teoremet til Pythagoras, som slår fast at innenfor en rektangel -trekant er kvadratet til hypotenusen (siden motstand mot høyre vinkel) lik summen av rutene til de gjenværende sidene.

Elementer av Euclid

Det mest fremtredende arbeidet som har blitt reddet siden eldgamle tider har vært studien Elementene, Fra Euclid de Alejandría (325 A.C. - 265 a.C.), laget i løpet av 300 -tallet til.C. Det er et verk av stor historisk verdi som har fungert som grunnlag for undervisning i matematikk i mer enn 2000 år.

Euclid

Elementene Det var en av de første bøkene og sammenstillinger av studier som forklarte matematiske prinsipper som kunne brukes på enhver situasjon. Inkluderer postulater, som er de grunnleggende prinsippene for geometri i deres arbeid. På den annen side er det de kvantitative prinsippene kjent som de grunnleggende forestillingene.

Euklidundervisning reduserte konstruksjonsinstrumenter innen geometri til bare to: en regel uten tiltak og et kompass. Dette genererte de tre klassiske problemene som ikke fant svar før det nittende århundre: sirkelen i sirkelen, dupliseringen av kuben og triseksjonen av en vinkel. 

Kan tjene deg: i hvilket århundre spanjolene erobret Tenochtitlán?

For de eldgamle var de to ideelle geometriske enhetene den rette linjen og sirkelen, så de fleste av de geometriske teoremene som ble foreslått var produktet av leting med disse instrumentene.

Geometri i astronomi

Geometrien hadde også fordel for grekerne når det gjelder studiet av stjernene. De beregnet bevegelsene gjennom observasjonen og laget geometriske planer av himmelen som etablerte jorden som et sentralt punkt, og både solen og månen og de andre planetene og enhetene som beveget seg rundt dem, og roterte i et sett med sirkler. 

Et av de mest innflytelsesrike bidragene var Almagest, Skrevet i det andre århundre d.C av claudio ptolemaios (100 d. C.- 170 d.C), en astronomisk traktatbeholder av Stars -katalogen. Det var den mest komplette teksten i hans tid og påvirket astronomiske studier på en transcendental måte til middelalderen veldig avansert. Det var en del av media som mest populariserte det geosentriske systemet, som hevdet at jorden var sentrum av universet.

Ptolemaios

Islamsk innflytelse

Mot IX -århundrene, da den arabiske verden var i sin store utvidelse, gjennomsyret mye av kulturen flere områder av vitenskap og kunst. De var gode fans av grekernes matematiske og filosofiske verk. 

En av de mest utforskede grenene innen deres behov var astronomi, for å finne den nøyaktige orienteringen der MECA skulle utføre setningene.

Etter studiene av euklid og andre bidrag som Ptolemaios, utviklet muslimer den stereografiske projeksjonen, det vil si projeksjonen av den himmelske sfære i flyet for å bruke det som et kart. Dette betydde fremgang angående studiet av trigonometri.

Blant de mest representative karakterene er Thābit Ibn Qurra (826/36-901) som laget relevante oversettelser av de gamle tekstene til Apollonius, Archimedes, Euclid og Ptolemy. Noen av disse er de eneste overlevende versjonene av eldgamle skrifter.

Utforskningene angående astronomisk geometri tillot også å opprette et av de mest representative instrumentene, Astrolabio, som forenklet de astronomiske beregningene av øyeblikket. I tillegg tillot dette instrumentet dem også å vite tid og endelig få veiledning til MECA. 

Det kan tjene deg: 8 skikker og tradisjoner av mixtekene

European Legacy Development

På det tolvte århundre, etter innsetting av grekernes klassiske læresetning. 

Dette vil gjøre plass for en ny læring i Europa som vil bli fremmet av renessansen. Omoppdagelsen av forestillinger som "bevisene" begynte, et konsept utviklet seg blant grekerne som var interessert i demonstrasjonen av postulatene i virkeligheten.

Geometri i kunst

Kunnskap gjenspeiles også i kunsten, som maleri eller arkitektur, siden geometri ville begynne å være en grunnleggende del av utviklingen av perspektiv i kunsten.

Filippo Brunelleschi (1377-1446), var den som klarte å utvikle det lineære perspektivet gjennom matematikk. Målet med denne teorien var å representere i et fly et tre -dimensjonalt rom fra hvordan det ble oppfattet av det menneskelige øyet. Dermed slår det fast at alle linjene på et bilde måtte konvergere eller finne en lekkasje for å generere følelsen av dybden. 

Filippo Brunelleschi. Kilde: I, Sailko/CC BY-S (http: // CreativeCommons.Org/lisenser/by-SA/3.0/)

Brunelleschi var den første som beskrev perspektivet som en vitenskapelig prosedyre, og dette fungerte som grunnlag for påfølgende jobber innen kunsten.

Innenfor andre eksempler på anvendelse av geometri på studiet av kunst og mennesket i seg selv, er arbeidet til Leonardo da Vinci (1452 -1519) i tegningen hans Vitruvio -mannen. Det er en studie basert på de mest perfekte proporsjonene for menneskekroppen gjennom en geometrisk analyse av dens struktur.

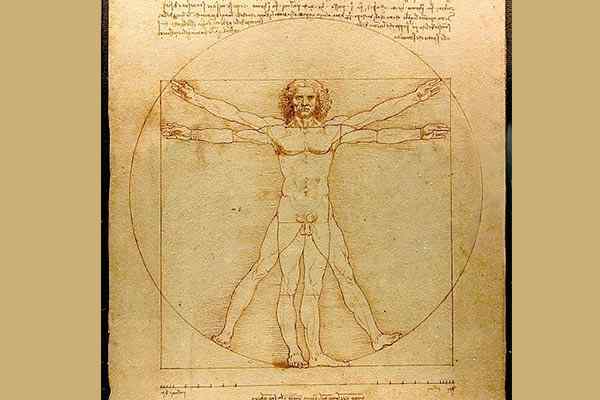The Man of Showcase av Leonardo da Vinci / Public Domain

Blant andre områder skiller arkitektur seg også ut, der forskjellige elementer som symmetri og balanse begynte å fremstå som grunnleggende egenskaper. Firkantede, rektangulære dører og vinduer, plassert på en balansert måte; Bruk av klassiske elementer av antikken som søyler, kupler og hvelv.

Trinn til moderniteten

Analysen av perspektiver og anslag under renessansen var en av insentivene til å vekke matematikernes interesse. Fra dette øyeblikket begynner mer solide og komplekse matematiske baser å være grunnlagt innen geometri.

Et av de viktigste verkene for moderniteten var arkitekten Girard-avvæpnet (1591-1661), som antok begynnelsen for projektive geometri. På den ene siden slo den fast at de parallelle linjene i en projeksjon skulle konvergere på et punkt på Infinity -linjen, det vil si horisonten.

Kan tjene deg: Tuxtepec -opprør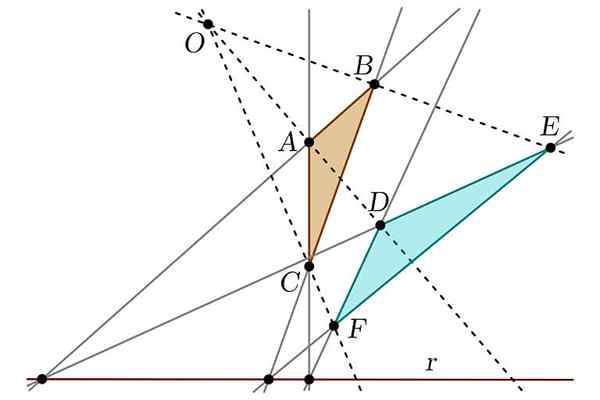Disarrisk teorem

På den annen side oppdaget han også hva som ville bli anerkjent som disaranger -teoremet, som etablerer forholdet mellom to figurer som kan betraktes som "projektive". Det var også ansvarlig for å forenkle Apollonius verk med hensyn til delene av en kjegle, noe som gjør analogier mellom denne figuren og sylinderen.

En annen stor begivenhet i perioden var opprettelsen av analytisk geometri gjennom studiene av René Descartes (1596-1650) og Pierre de Fermat (1601-1665) uavhengig av. Dette er studiet av geometri gjennom bruk av et koordinatsystem. 

René Descartes jobber på skrivebordet ditt. Wikimedia Commons

Ikke -euclidian geometri

Mot 1700- og 1800 -tallet begynte studier i ikke -euclidian geometri. Spesielt var Gauss, Johann Boleai og Lobachevsky, som fant ut at det femte postulatet av Euclid, kjent som parallell postulat, ikke kunne verifiseres.

På denne måten utviklet de en type geometri der dette postulatet ble kvalifisert som usant. Denne nye formen var vellykket ved å gi tilfredsstillende resultater i geometri -stiler som ikke nødvendigvis oppfylte alle Euclid -postulater. Dermed ble hyperbolsk geometri og elliptisk geometri født senere.

Det er verdt å fremheve arbeidet til Leonhard Euler (1707-1783) på 1700-tallet, med hensyn til utviklingen av matematisk notasjon. Deretter ville det tjuende århundre føre til utvikling av mer spesifikke geometrifelt blant dem:

-Algebraisk geometri: Det er en gren av matematikk som kombinerer abstrakt algebra og analytisk geometri.

-Endelig geometri: Det er et geometrisk system som består av en begrenset mengde poeng, det vil si at de har en slutt eller grense, og derfor kan de måles.

-Digital geometri: Det er en gren av informatikk at studiet av algoritmer og datastrukturer som kan representeres i geometriske termer. 

Referanser

1. (2016) Det som gjorde euklide elementer til den eneste boken som kan konkurrere med Bibelen. BBC. BBC kom seg.com
2. De tre klassiske problemene med gresk matematikk. University of Antioquia. Gjenopprettet etter undervisning.du.Edu.co
3. Heilbron J.L (2020). Geometri. Encyclopædia Britannica. Gjenopprettet fra Britannica.com
4. Historie om geometri. Wikipedia, gratis leksikon. Innhentet fra.Wikipedia.org
5. Analytisk geometri. Wikipedia, gratis leksikon. Innhentet fra.Wikipedia.org
6. (2017) Geometri og matematikk i renessansen. Gjenopprettet fra ukessays.com
7. Sáiz a. Lineært perspektiv i Brunelleschi. University of Valencia. UV kom seg.er
8. Redaktørene av Encyclopaedia Britannica (2019). Renessansearkitektur. Encyclopædia Britannica. Gjenopprettet fra Britannica.com
9. Andersen K (2020). Girard avvæpnet. Encyclopædia Britannica. Gjenopprettet fra Britannica.com
10. (2011) En interessant introduksjon til beregningsgeometri. Hentet fra Gaussians.com