Trigonometriske identiteter (eksempler og øvelser)

De trigonometriske identiteter Dette er forhold mellom trigonometriske grunner, som er sanne for enhver verdi av variabelen. For eksempel:

Tan θ = sin θ /cos θ

Det er en trigonometrisk identitet som relaterer tre årsaker til vinkelen θ, tangenten, brystet og kosinus av nevnte vinkel.

Figur 1. Noen trigonometriske identiteter som er mye brukt i beregning. Kilde: f. Zapata.

Denne identiteten er sann for all verdi, bortsett fra de som gjør 0 nevneren. Cos θ er 0 for θ = ± π/2, ± 3π/2, ± 5π/2 ... et annet eksempel på trigonometrisk identitet er:

sin x . SEC X . CTG x = 1

[TOC]

Demonstrasjon

Det er to grunnleggende måter å demonstrere at en trigonometrisk identitet er sann:

1- Transformerer et av likestillingsmedlemmene til det andre, gjennom praktiske algebraiske manipulasjoner.

2- Utvikle begge medlemmer av likhet separat, inntil de respektive endelige uttrykk for hver er nøyaktig de samme.

I den foreslåtte identiteten skal vi transformere venstre side av likhet, som vi uttrykker CTG X og SEC X for bryst og kosinus som følger:

Ctg x = cos x / sen x

Sec x = 1 /cos x

Vi erstatter dette uttrykket på venstre side av identitet og forenkle:

sin x . (1/cos x). (cos x / sen x) = (sin x. cos x / cos x . sin x) = 1

Og sannheten i identiteten er allerede bevist.

Typer trigonometriske identiteter

Det er flere typer trigonometriske identiteter. Neste vil vi kort beskrive de viktigste:

- Grunnleggende trigonometriske identiteter

Vi skiller to typer grunnleggende identiteter:

I) De som kommer til uttrykk gjennom de grunnleggende årsakene, kosinus og tangens:

• Sec x = 1 /cos x
• Skade x / 1 / sin x
• Ctg x = 1 / tg x
• Tg x = sin x /cos x
• Ctg x = cos x / sen x

I) de som er avledet fra paritet. Vi vet gjennom grafen at Sen X er en merkelig funksjon, noe som betyr at:

Kan tjene deg: 60 deling

sin (-x) = - sin x

For sin del er Cos X et par, derfor:

cos (-x) = cos x

Så:

tg (-x) = sen (-x) / cos (-x) = -sen x / cos x

På samme måte:

• cotg (-x) = -ctg x
• sek (-x) = sek x
• skade (-x) = - skade x

- Pythagorean identiteter

Det er de som er oppnådd fra anvendelsen av Pythagoras -teoremet til rektangelets trekant av katter A og B og Hypotenusa C. La oss se:

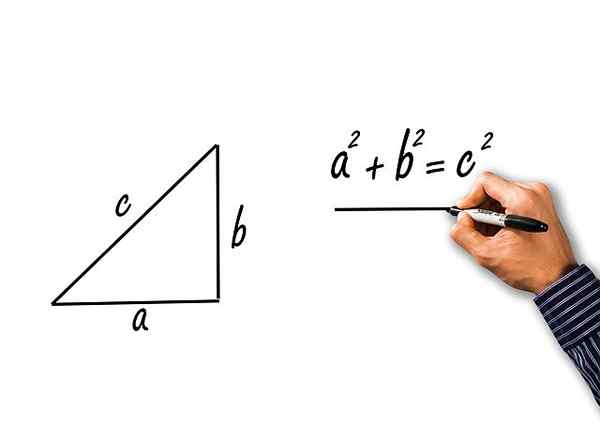Figur 2.- Fra Pythagoras teorem oppnås de tre pytagoreiske trigonometriske identitetene. Kilde: Pixabay.

Pythagoras 'teorem uttaler at:

c² = a² + b²

Dele alt mellom C²:

c² / c² = (a² / c²) + (B² / c²)

Begrepet til venstre er 1 og husker at bihule og kosinus i den akutte vinkelen α er definert som:

sin α = a/c

cos α = b/c

Resultat:

1 = (sin α)² + (cos α)²

Denne identiteten er kjent som grunnleggende identitet.

Prosedyren kan utføres ved å dele mellom² og b², som gir opphav til to identiteter til:

Sek² α = 1 + tg² α

Har² α = 1 + CTG² α

- Formler for kosinus og brystets bryst/subtraksjon av vinkler

De viktigste trigonometriske identitetene for kosinus, bryst og tangent av summen og subtraksjon er følgende:

Sen -demonstrasjon (α + β) og COS (α + β)

Disse identitetene kan demonstreres geometrisk eller også gjennom Euler -formelen:

og^iα = cos α + i sin α

La oss se på hva som skjer med formelen når vi erstatter summen av to vinkler α og β:

og^{I (α +β)} = cos (α + β) + i sin (α + β)

Dette uttrykket er sammensatt, dens virkelige del er COS (α + β) og dens imaginære del er I Sin (α + β). Vi holder dette resultatet for å bruke det senere og fokusere på å utvikle den eksponentielle delen:

og^{I (α +β)} = e^iα ⋅ e^Ip = (cos α + i sin α) . (cos β + i sin β) =

Kan tjene deg: sekskantet prisme

6

Den virkelige delen av dette uttrykket er den som ikke multipliseres av den imaginære enheten "I":

cos α cos β - sen α. Sen β

Den imaginære delen er derfor:

I (Cos αSen β + sen α⋅COS β)

For at to komplekse uttrykk skal være de samme, må den virkelige delen av den ene være lik den virkelige delen av den andre. Det samme gjelder imaginære deler.

Vi tar resultatet reddet og sammenligner det med dette:

cos α. cos β - sen α. sin β = cos (α + β)

i (cos ⋅sen β + sen α⋅cos β) = i sin (α + β)

sin (α + β) = (cos α. sin β + sen ⋅ cos β)

- Formler for dobbeltvinkelen

I de forrige formlene tar vi β = α og utvikler:

sin (α + α) = sen 2 α = sen α⋅Cos α + cos α. sin α = 2⋅ sin α ⋅ cos α

COS (α + α) = cos 2 α = cos α⋅COS α - Sen α⋅sen α = cos² α - Sen ² α

Tg (α + α) = Tg 2 α = [Tg α + Tg α] / [1- Tg α⋅tg α] = 2TG α / 1- Tg² α

Hvis i det andre uttrykket er cos erstattet² α = 1 - Sen² α oppnås:

cos 2 α = cos² α- (1- cos² α) = 2 cos² α -1

- Halvvinkelformler

I dette siste uttrykket erstatter vi α med α/2, gjenstår følgende:

cos α = 2 cos ²(α/2) -1

Lysning:

Løste øvelser

- Oppgave 1

Vis det:

Løsning

Vi skal jobbe algebraisk begrepet igjen slik at det ser ut som riktig. Som i riktig begrep vises Sen X, er det første trinnet å uttrykke COS²X Når det gjelder Sen X slik at alt er i form av den samme trigonometriske grunnen:

Det kan tjene deg: brøkdel tilsvarer 3/5 (løsning og forklaring)

Da 1 - Sen er faktor² x for å være en forskjell på perfekte firkanter. For å gjøre dette, rydder det fra den grunnleggende identiteten:

Cos²X = 1 - Sen² x

1 - Sen² x = (1- sin x) (1+senx)

Og faktoriseringen i det opprinnelige uttrykket erstattes:

Begrepet (1- Senx) er forenklet og en likhet gjenstår:

1 + sen x = 1 + senx

- Oppgave 2

Løs følgende trigonometriske ligning og gi løsningen for verdier mellom 0 og 360º:

Tg x + sek² x = 3

Løsning

I løpet av venstre er det to trigonometriske grunner, derfor må du redusere alt til en, for å kunne fjerne det ukjente. Begrepet sek² X uttrykkes gjennom en av de pytagoreiske identitetene:

Sek² α = 1 + tg² α

Ved å erstatte ligningen:

Tg x + 1 + tg² x = 3

Omorganisere vilkårene:

Tg² x + tg x + 1 = 3

Denne ligningen løses ved å endre variabelen:

tg x = u

eller² + U + 1 - 3 = 0 → u² + U - 2 = 0

Denne andre gradsligningen løses enkelt ved faktorisering:

(U +2) (u-1) = 0

Derfor u₁ = -2 og u₂ = 1, tilsvarer:

Tg x₁ = -2

Tg x₂ = 1

Endelig:

x₁ = ARCTG (-2) = 296.6

x₂  = ARCTG (1) = 45º

Referanser

1. Carena, m. 2019. Preuniversity Mathematics Manual. National University of the Coast.
2. Figuera, J. 1999. Matte. 1. Diversifisert. Bolivarian Collegiate Editions.
3. Hoffman, J. Valg av matematikkproblemer. Volum 4.
4. Jiménez, r. 2008. Algebra. Prentice Hall.
5. Wikipedia. Trigonometri -identiteter og formler. Gjenopprettet fra: er.Wikipedia.org.
6. Zapata, f. 4 måter å løse en andre grads ligning på. Gjenopprettet fra: Francesphysics.Blogspot.com.
7. Zill, d. 1984. Algebra og trigonometri. McGraw Hill.