Historie med trigonometri fra sin opprinnelse

De Trigonometri historie Det refererer til settet med fakta og fremskritt som skjedde rundt denne grenen av matematikk fra dens opprinnelse til de siste hendelsene.

Når du tar en kort tur gjennom historien, er det tydelig at denne vitenskapen ble født som svar på problemene som de gamle astronomene og navigatørene står overfor for å analysere forskyvningen av stjernene på himmelen.

Begrepet vises for første gang i boken Trigonometriae Libri Quinque, skrevet av tysk matematiker og forsker Pitiscus Bartolomé (1561-1613). Via Wikimedia Commons.

På samme måte oppstår ordet trigonometri fra sammensetningen av to greske ord: Trigonon (trekant) og METRON (utstrekning). Begrepet vises for første gang i boka Trigonometriae Libri Quinque, Skrevet av tysk matematiker og forsker Pitiscus Bartolomé (1561-1613).

På denne måten viser ordets etymologi at trigonometri er studien forholdene mellom vinklene til en trekant og segmentene eller linjene som danner den.

[TOC]

Begynnelsen av trigonometri

De første trinnene i trigonometrien ble utført av mennesket når de ble promotert av behovet for å kjenne og analysere stjernenes bevegelse.

Det vil si at mennesket utviklet trigonometri fordi det ble funnet i situasjoner der det var umulig å gjøre målinger direkte, siden for å beregne stjernene var mer komplekse matematiske verktøy påkrevd.

- Studier i Babylon

Mud Table skrevet av de av babylonikere kalt Plimpton 322. Via: Wikimedia Commons

Studier viser at for mer enn 3 siden.000 år Babylonikere håndterte allerede begrepet vinkel og trigonometriske grunner, det vil si at de var i stand til å etablere forholdet mellom sidene og trekantene i trekantene og trekantene.

For eksempel et gjørmebord - skrevet av babylonians - kalt Plimpton 322 (1800 a. C.) viser en rekke kolonner og rader som inneholder tall i kuleformskriving. I følge forskning utført av noen eksperter, representerer dette nettbrettet det som ser ut til å være en serie trigonometriske funksjoner.

Kan tjene deg: Hva er retningslinjen? (Geometri)

Babylonerne var kjent med konseptene som ga opphav til Pythagoras 'teorem (569-474 a.C) Og de forsto prinsippet sitt.

På samme måte visste de også at teoremet ble tilskrevet Thales of Miletus (695-546 til.C), som indikerer at hver rett, tegnet parallelt med siden av en trekant, dannes med de to andre sidene en annen trekant som ligner på den første trekanten.

- De gamle egypterne

De gamle egypterne klarte å opprettholde skråningen jevnt på hver av pyramide ansiktene. Via: Pixabay

Selv om det ikke er aktuelt å snakke om trigonometri i den generelle sfæren av egyptisk matematikk, er det ingen tvil om at denne sivilisasjonen håndterte visse trigonometriske begreper.

Dette skjer fordi når egypterne vurderer de store bygningene som er laget av egypterne, for eksempel pyramider, kan det konkluderes med at de hadde litt kunnskap om trigonometri.

En grunnleggende ingeniørvanskelighet som egypterne står overfor - og det løste seg fantastisk.

For dette brukte de et konsept de kalte "seqt", og det tilsvarer det vi forstår i dag som en skråning av en skrå flat overflate.

I tillegg er egypterne for å foreta målinger på de vertikale overflatene som brukes som en enhet "albuen" og i horisontalt "hånden", som tilsvarte 1/7 i albuen. På denne måten beregnet de seqt eller i påvente av i de forskjellige bygningene. For eksempel, i pyramiden til Jufú (Queope) er SEQT 5 1/2 hender per albue.

- Antikkens Hellas og strengbordet

All kunnskap om babylonerne og de gamle egypterne ga til Hellas, der matematikeren og astronomen i NICEA (190-120 ble fremhevet (190-120. C), som regnes som faren til trigonometri. Hiparco opprettet “Strings” -tabellene, som han klarte å løse problemene med flate trekanter.

Nicea Hiparco - Kilde: overført fra.Wikipedia til Commons av Maksim - under offentlig domene

For å lage dem brukte den en omkrets med en viss radius (en radius er avstanden mellom midten av en sirkel og et hvilket som helst punkt i omkretsen).

Kan tjene deg: Betinget sannsynlighet: Formel og ligninger, egenskaper, eksempler

Deretter fortrengte det radius for å definere forskjellige vinkler; Mens du gjorde dette, var det å peke i bordet på linjen som ble avgrenset på sidene av vinkelen og omkretsen.

Disse "strengene" viste seg å være forløpere for tabellene til de trigonometriske funksjonene som vi bruker i dag.

- India bidrag

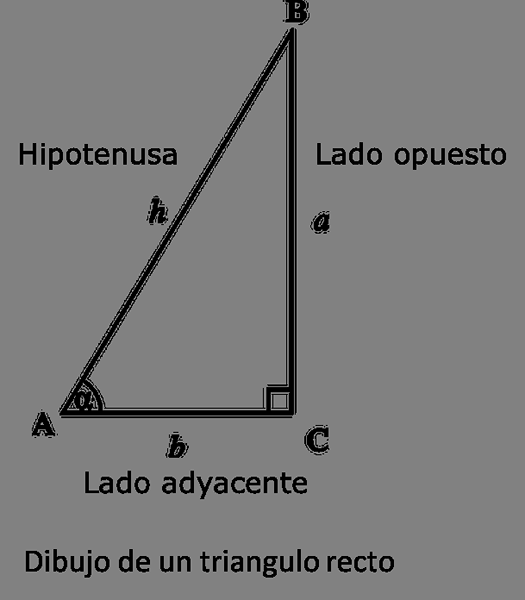Tegning av en høyre trekant.

I likhet med Hellas lærde utviklet astronomer i India også et trigonometrisk system, men i motsetning til grekerne baserte disse astronomene sin analyse på "sinus" -funksjonen i stedet for å bruke strengene.

Imidlertid er "sinus" -funksjonen uttrykt av disse astronomene ikke den som brukes i dag; Denne funksjonen var ikke en andel (som brukt i dag), men lengden på motsatt side av en vinkel på en rektangel -trekant hvis hypotenuse er kjent.

- Arabia og trigonometriske funksjoner

På slutten av det åttende århundre begynte arabiske astronomer, påvirket av trigonometri -studier utført av folkene i Hellas og India, viktige studier på forhold mellom vinkler og deres sider.

På denne måten, på slutten av det 10. århundre, løftet de de velkjente funksjonene til bryst, kosinus, tangent, cotangent, tørking og høst.

De oppdaget og bekreftet også primære trigonometri -teoremer, som brukes i analysen av flate og sfæriske trekanter. I tillegg antydet arabiske matematikere bruken av en verdi ("1") for radio (r = 1), noe som ga opphav til moderne verdier av trigonometriske funksjoner.

- Bidrag fra Vesten

Johann Müller kjent som Regiomontanus (1436-1476). Oppnådd systematisering og generalisering av trigonometriske metoder brukt i geometri -området. Via: Wikimedia Commons

Matematikken i Vesten, spesielt mellom det tolvte og femtende århundre, var sterkt påvirket av postulatene fra det gamle Hellas, India og araberne.

Kan tjene deg: chi-square (²): distribusjon, hvordan det beregnes, eksempler

I løpet av denne tiden var de avgjørende i området Trigonometry-bidragene fra Johann Müller, også kjent som Regiomontanus (1436-1476). Denne matematikeren oppnådde systematisering og generalisering av trigonometriske metoder som ble brukt i geometriområdet.

Regiomontanus utdypet og publiserte en traktat han kalte Av Triangulis Omnimodis Libri Quinque, som var sammensatt av fem bøker og totalt 131 sider.

I denne boken regulerte han alle begrepene flat og sfærisk trigonometri, som deretter ble brukt av viktige astronomer som: Nicolás Copernic.

- Trigonometri syttende og attende århundre

I løpet av det syttende århundre hadde studiene om trigonometriske beregninger fremgang takket være bidragene fra matematikere som Scotch John Napier (1550-1617), som løftet forskjellige metoder for oppløsning av sfæriske trekanter.

John Napier. Kilde: av Encard av Samuel Freeman (1773-1857) [Public Domain], via Wikimedia Common

Senere, på 1700-tallet, var bidragene fra den sveitsiske matematikeren Leonhard Euler (1707-1783) avgjørende, siden studiene hans la grunnlaget for moderne trigonometri ved å introdusere notasjonen som for tiden brukes til trigonometriske funksjoner.

I tillegg klarte Euler å definere den eksponentielle funksjonen og oppdaget hans forhold til trigonometriske funksjoner, som tillot ham å beskrive egenskapene til trigonometri.

Deretter letter Sir Isaac Newton (1643-1727) ved å oppfinne differensial og integral beregning. På denne måten ble trigonometri en del av den matematiske analysen, der i dag spiller en grunnleggende rolle.

Illustrasjon av Sir Isaac Newton

Referanser

1. Mansfield, Daniel. Wildberger, n. (2017). Plimpton 322 er babylonsk eksakt sexagesimal trigonometri. Hentet 20. mai 2020 fra: Scientedirect.com
2. Jimenez s. (2017). Historie om trigonometri og dens applikasjoner. Hentet 23. mai 2020 Deedu
3. Pérez, v. (2010). Trigonometri historie. Hentet 22. mai 2020 fra: Laguia2000.com
4. S.TIL. (s.F.) Trigonometri. Hentet 23. mai 2020 fra: Blogspot.com
5. Merlet, Jean-Pierre (2004). Et notat om historien til trigonometriske funksjoner. Hentet 22. mai 2020 fra: Nett
6. Adamek, t., Penkalski, k., Valentine, g. (2005). Trigonometrihistorien. Hentet 23. mai 2020 fra: Citseseerx.Ist.PSU.Edu/