Homokedisitet hva som er, viktighet og eksempler

De Homokedisitet I en prediktiv statistisk modell forekommer det hvis i alle datagrupper av en eller flere observasjoner, varianten av modellen med hensyn til de forklarende (eller uavhengige) variablene forblir konstant.

En regresjonsmodell kan være homokedastisk eller ikke, i så fall snakker vi om heterocedisitet.

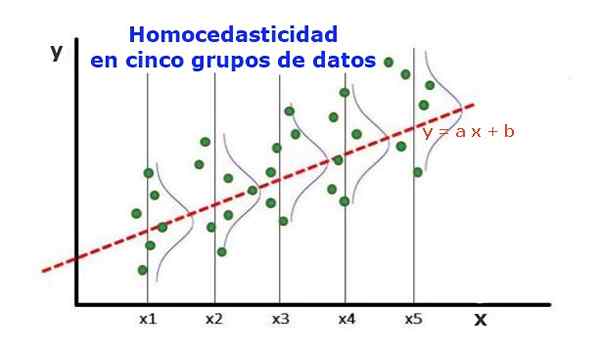
Figur 1. Fem datagrupper og regresjonsjustering av settet. Variansen angående den forutsagte verdien er den samme i hver gruppe. (Upav-Library.org)

En statistisk regresjonsmodell av flere uavhengige variabler kalles homocedastic, bare hvis variansen av den forutsagte variable feilen (eller standardavviket til den avhengige variabelen) forblir ensartet for forskjellige grupper av de forklarende eller uavhengige variablene.

I de fem datagruppene i figur 1 er variansen blitt beregnet i hver gruppe, med hensyn til verdien estimert av regresjonen, og er å være den samme i hver gruppe. Det antas også at dataene følger normalfordelingen.

På et grafisk nivå betyr det at punktene er like spredt eller spredt rundt den forutsagte verdien av regresjonsjusteringen, og at regresjonsmodellen har samme feil og gyldighet for området for den forklarende variabelen.

[TOC]

Viktigheten av homokedisitet

For å illustrere viktigheten av homokedastisitet i prediktiv statistikk, er det nødvendig å kontrast til det motsatte fenomenet, heterokedisitet.

Homokedastisitet kontra heterocedisitet

Når det gjelder figur 1, der det er homokedisitet, blir det oppfylt at:

Var ((y1-y1); x1) ≈ var ((y2-y2); x2) ≈ ... var (y4-y4); x4)

Der VAR ((YI-II); XI) representerer variansen, representerer paret (XI, Yi) et faktum av gruppe I, mens Yi er verdien som forutsier regresjonen for den gjennomsnittlige XI-verdien til gruppen. Variansen av dataene fra gruppe I beregnes som følger:

Var ((yi -ii); xi) = ∑j (yij - yi)^2/n

Tvert imot, når heterocedisitet oppstår, kan det hende at regresjonsmodellen ikke er gyldig for hele regionen der den ble beregnet. Figur 2 viser et eksempel på denne situasjonen.

Kan tjene deg: Hva er indre alternative vinkler? (Med øvelser)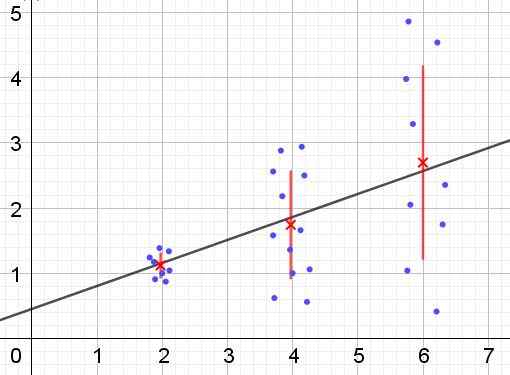 Figur 2. Datagruppe som har heterokedisitet. (Egen utdyping)

I figur 2 er tre datagrupper og settet med settet representert ved en lineær regresjon. Det skal bemerkes at dataene i den andre og i den tredje gruppen er mer spredt enn i den første gruppen. Grafen i figur 2 viser også gjennomsnittsverdien for hver gruppe og dens feillinje ± σ, og er σ standardavviket til hver datagruppe. Det må huskes at standardavviket σ er kvadratroten til variansen.

Det er klart at i tilfelle av heterocedisitet, endres feilen i regresjonsestimeringen i verdiene for den forklarende eller uavhengige variabelen, og i intervallene der denne feilen er veldig stor, er prediksjonen ved regresjon upålitelig eller ikke relevant.

I en regresjonsmodell må feil eller avfall (y -y) distribueres med like varians (σ^2) gjennom Independent Variable Values ​​Interal. Det er av denne grunn at en god regresjonsmodell (lineær eller ikke -lineær) må bestå homokedastisitetstesten. 

Homokedisitetstester

Punktene vist i figur 3 tilsvarer dataene fra en studie som søker et forhold mellom prisene (i dollar) av husene, avhengig av størrelse eller område i kvadratmeter.

Den første modellen som øves er den av en lineær regresjon. For det første bemerkes det at bestemmelseskoeffisienten r^2 av justeringen er ganske høy (91%), så det kan tenkes at justeringen er tilfredsstillende.

Imidlertid kan to regioner skilles tydelig fra justeringsgrafen. En av dem, den til høyre låst i en oval, møter homokedastisitet, mens regionen til venstre ikke har noen homokedastisitet.

Kan tjene deg: karakter av et polynom: hvordan det bestemmes, eksempler og øvelser

Dette betyr at prediksjonen av regresjonsmodellen er tilstrekkelig og pålitelig i området mellom 1800 m^2 til 4800 m^2, men veldig utilstrekkelig utenfor denne regionen. I det heterocediske området er ikke bare feilen veldig stor, men også dataene ser ut til å følge en annen trend som er forskjellig fra den foreslåtte av den lineære regresjonsmodellen.

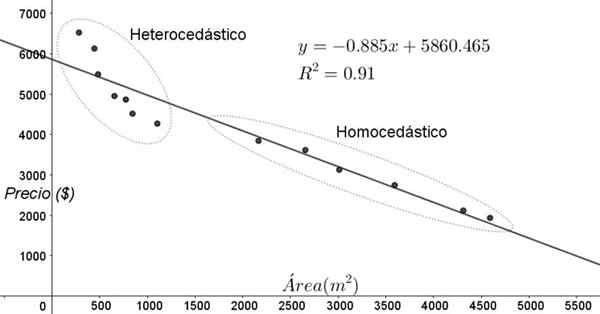Figur 3. Boligpriser vs område og prediktiv modell ved lineær regresjon, og viser homokedastisitet og heterocedisitetsområder. (Egen utdyping)

Data -spredningsgrafen er den enkleste og mest visuelle testen av deres homokedastisitet, men noen ganger er det ikke så tydelig som i eksemplet vist i figur 3, er det nødvendig å ty til grafikk med tilleggsvariabler.

Standardiserte variabler

Med det formål å skille områdene der homokedastisitet blir oppfylt og der ikke, blir de standardiserte variablene ZREs og Zreded introdusert:

Zres = abs (y - y)/σ

Zpred = y/σ

Det skal bemerkes at disse variablene avhenger av regresjonsmodellen som er brukt, siden det er verdien av regresjonsprediksjon. Nedenfor er Zres vs Zred -spredningsgrafen for det samme eksemplet:

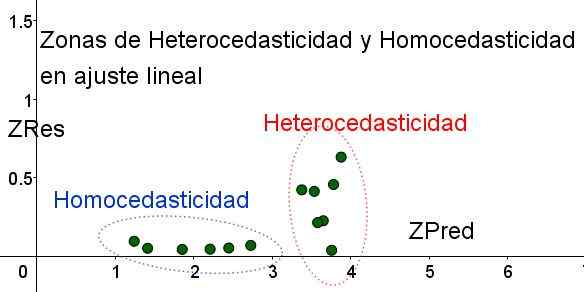Figur 4. Det skal bemerkes at i homokedastisitetssonen forblir ZRES ensartet og liten i prediksjonsregionen (egen utdyping).

I grafen i figur 4 med de standardiserte variablene, er området der den gjenværende feilen er lite og ensartet tydelig separert, med hensyn til den som ikke gjør det. I det første området blir homokedastisitet oppfylt mens restfeilen er veldig variabel og stor.

En regresjonsjustering brukes på samme datagruppe 3. Resultatet vises i følgende figur:

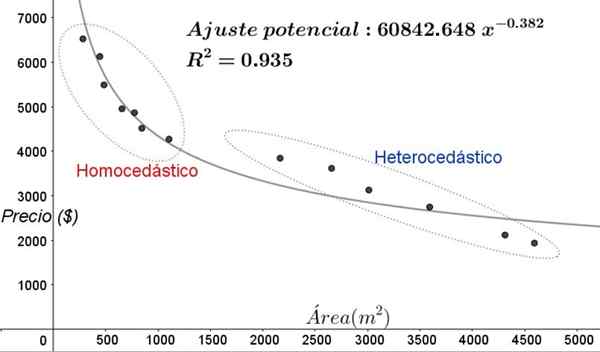Figur 5. Ny homokedastisitet og heterocedisitetsområder i datajustering med en ikke-lineal regresjonsmodell. (Egen utdyping).

I grafen i figur 5 bør de homokediske og heterokedikastiske områdene være tydelig lagt merke til. Det skal også bemerkes at disse områdene ble utvekslet med hensyn til de som ble dannet i den lineære justeringsmodellen.

Kan tjene deg: typer vinkler, egenskaper og eksempler

I grafen i figur 5 er det tydelig at selv når det er en bestemmelseskoeffisient for justeringen ganske høy (93,5%), er modellen ikke egnet for hele intervallet til den forklarende variabelen, siden dataene for verdier eldre enn 2000 M^2 har heterocedasticity.

Ikke -fotografiske homokedastisitetstester

En av de mest brukte ikke -fotografiske testene for å bekrefte om homocedasticity er oppfylt er den Breusch-pagen test.

Alle detaljer om denne testen vil ikke bli gitt i denne artikkelen, men dens grunnleggende egenskaper og trinnene til det samme er vidt skissert:

1. Regresjonsmodellen brukes på N -dataene og variansen av den samme beregnes med hensyn til verdien estimert av modellen σ^2 = ∑j (yj - y)^2/n.
2. En ny variabel ε = ((yj - y)^2) / (σ^2) er definert
3. Den samme regresjonsmodellen brukes på den nye variabelen og dens nye regresjonsparametere beregnes.
4. Chi Square Critical Value (χ^2) bestemmes, dette er halvparten av summen av rutene nytt avfall i ε -variabelen.
5. Chi Square distribusjonstabell brukes med tanke på nivået av betydning på x -aksen (vanligvis 5%) og antall frihetsgrader (#av regresjonsvariabler unntatt enheten), for å oppnå verdien av styret.
6. Den kritiske verdien oppnådd i trinn 3 blir sammenlignet med verdien som er funnet i tabellen (χ^2).
7. Hvis den kritiske verdien er under tabellen har du nullhypotesen: det er homokedisitet
8. Hvis den kritiske verdien er over tabellen, har du den alternative hypotesen: det er ingen homokedastisitet.

De fleste av de statistiske datamaskinpakkene som: SPSS, Minitab, R, Python Pandas, SAS, Statgraphic og flere andre inneholder homokedastisitetstesten av Breusch-Pagan. En annen test for å bekrefte ensartethet av varians Levene test.

Referanser

1. Box, Hunter & Hunter. (1988) Statistikk for forskere. Jeg vendte redaktører.
2. Johnston, J (1989). Econometrics Methodics, Vicens -ives redaksjoner.
3. Murillo og González (2000). Økonometry manual. University of Las Palmas de Gran Canaria. Hentet fra: ULPGC.er.
4. Wikipedia. Homokedisitet. Gjenopprettet fra: er.Wikipedia.com
5. Wikipedia. Homoscedasticity. Hentet fra: i.Wikipedia.com