Lagrange interpolasjon

Hva er Lagranges interpolasjon?

Lagranges interpolasjon er en numerisk metode for tilnærming av funksjoner, som gjør bruk av et polynom som passerer gjennom visse kjente punkter i funksjonen som er ment å tilnærme seg.

Hvis den omtrentlige funksjonen er myk, selv utenfor de gitte eller kjente verdiene, tar polynom verdier nær de av funksjonens funksjon, spesielt hvis disse verdiene er mellom de gitte punktene. Det er grunnen til at polynom blir ansett som en god tilnærming til funksjonen.

Figur 1.- Formel for å bygge LaGrange Polynomials. Kilde: f. Zapata.

Anta at du vil tilnærme en funksjon f (x) hvorav bare verdiene deres er kjent i noen x-_Yo-, med Yo fra 0 før N-1. Det vil si at de kjenner hverandre n poeng (x-_Yo, og_Yo) med og_Yo = f (x_Yo), Hvor indeksen Yo Går fra 0 før N-1.

I Lagrange -interpolasjonsmetoden, polynomet som nærmer seg funksjonen f (x) Det er et polynom P (x) av grad N-1, bygget av den lineære kombinasjonen av n Polynomer L_Yo(x) av grad N-1. Dette er Lagrange polynomer, som uttrykkes som følger:

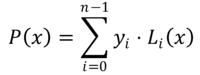
Verdiene til og_Yo De representerer ordinatene som tilsvarer abscissa x_Yo Hvor funksjonen f (x) Det er kjent, det vil si: og_Yo = f (x_Yo).

Lagrange polynomer

Gjennom lineære kombinasjoner mellom dem fungerer LaGrange Polynomials som et grunnlag for å bygge polynom i klassen N -1 som vil tjene til å interpolere n kjente poeng.

Notasjonen for polynomer er l_Yo(x), med indeks I i området fra 0 til n-1. Formelen for å etablere LaGrange -polynomer er som følger:

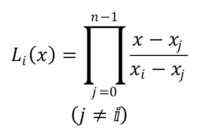
Symbolet som er vist indikerer at produktorien til n -1 monomialer må utføres, med start fra polynomet J = 0.

Kjennetegn på LaGrange Polynomials

1.- Lagrange -polynomer er nøyaktig de samme som enheten når de evalueres i abscissa som tilsvarer deres indeks, det vil si:

L_Yo(x_Yo) = 1

2.- De blir kansellert i abscissa av interpolasjonspunktene med indeks som er forskjellig fra samme polynom:

Kan tjene deg: Beskrivende statistikk: Historie, egenskaper, eksempler, konsepter

L_Yo(x_J) = 0, med i ≠ j.

3.- Å ta andre abscissa -verdier forskjellig fra interpolasjonspunkter, er Lagrange -polynomer verdier mellom -1 og +1.

4.- For å skaffe Lagrange -polynomer, er det bare nødvendig å kjenne abscissa for punktene til Interpoch.

Andre -graders Lagrange Polynomials

Andre graders Lagrange -polynomer er de som brukes hyppigst når du vil gjøre en trepunktsinterpolasjon.

Anta at den interpolare funksjonen er kjent i tre punkter, som er:

(x₀,og₀); (x₁, og₁); (x₂, og₂)

Deretter dine tilsvarende Lagrange -polynomer L₀, L₁ og L₂ De blir slik:

L₀(x) = [(x - x₁) / (X₀ - x₁)] [(x - x₂) / (X₀ - x₂)]

L₁(x) = [(x - x₀) / (X₁ - x₀)] [(x - x₂) / (X₁ - x₂)]

L₂(x) = [(x - x₀) / (X₂ - x₀)] [(x - x₁) / (X₂ - x₁)]

Det er verdt å merke seg at L₀(x₀) = L₁(x₁) = L₂(x₂) = 1, samtidig som L_Yo(x_J) = 0 så lenge som Yo≠ J.

Interpolasjonspolynom av andre grad

Det er viktig å merke seg at i Lagranges interpolasjonspolynom er ordinatene for interpolasjonspunkter Lagrange Polynomial Factors.

På denne måten, når polynomene er oppnådd for visse verdier av abscissa, tjener de til å beregne interpolasjonspolynomet av forskjellige funksjoner, forutsatt at bestilt i den tidligere faste abscissa er kjent.

I tilfelle av en interpolering av andre klasse:

P (x) = f (x₀) L₀(x) + f (x₁) L₁(x) + f (x₂) L₂(x)

Og p (x) nærmer seg funksjonen f (x) i intervallet (x₀, x₂).

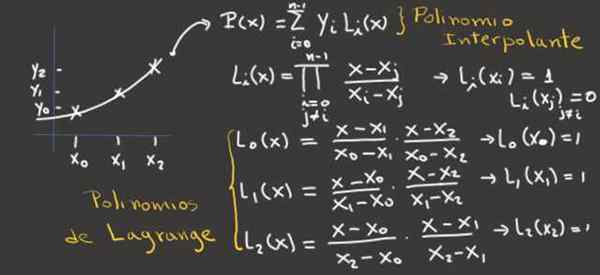Figur 2.- Dette bildet viser hvordan du kan oppnå Lagrange -polynomene for tre interpolasjonspunkter og fra dem, interpoling -polynomet. Kilde: f. Zapata.

Eksempler

Eksempel 1

Finn Lagrange -polynomene som tilsvarer tre abscissa -poeng x₀= 0, x₁= 1 og x₂= 2.

Som det fremgår av forrige avsnitt, vil disse polynomene være:

Kan tjene deg: Overjektive funksjon: Definisjon, egenskaper, eksempler

L₀(x) = [(x - 1) / (0 - 1)] [(x - 2) / (0 - 2)] = - (x -1) ⋅ (-½) (x - 2) = ½ ( x² - 3x + 2)

L₁(x) = [(x - 0) / (1 - 0)] [(x - 2) / (1 - 2)] = x ⋅ (-1) (x - 2) = - x² + 2x

L₂(x) = [(x - 0) / (2 - 0)] [(x - 1) / (2 - 1)] = (½) x ⋅ (x - 1) = (½) (x² - x)

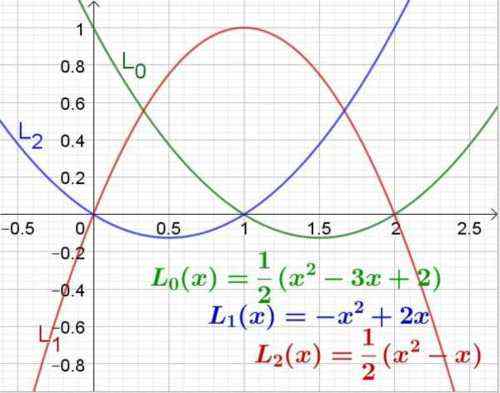Figur 3. Lagrange polynomer for abscissa -verdier 0, 1 og 2. Kilde: f. Zapata.

Eksempel 2

Du vil tilnærme funksjonen f (x) = Arcan (x) I intervallet [0, 2]. Av denne funksjonen er det bare kjent at verdiene deres er kjent for x₀= 0, x₁= 1 og x₂= 2, som er henholdsvis og₀= 0, og₁= π/4 = 0,785 og og₂= 1,107.

Derfor må du finne det interpoling polynomet P (x) nærmer seg f (x) I det indikerte intervallet.

I eksempel 1 er Lagrange -polynomer allerede bestemt for abscissa -verdiene som er angitt i denne uttalelsen, så det er ikke nødvendig å gjenta beregningen. Interpoling Polynomial vil nå være:

P (x) = f (x₀) L₀(x) + f (x₁) L₁(x) + f (x₂) L₂(x)

Som tilsvarer:

P (x) = y₀ L₀(x) + og₁ L₁(x) + og₂ L₂(x)

I dette spesifikke tilfellet er det:

P (x) = 0 ∙ (½) (x² - 3x + 2) + 0.785 ∙ (- x² + 2x) + 1,107 ∙ (½) (x² - x)

Ovennevnte er forenklet til:

P (x) = 0,785 ∙ (- x² + 2x) + 1,107 ∙ (½) (x² - x)

Og til slutt gjenstår:

P (x) = -0,2315 ∙ x² + 1.0165 ∙ x

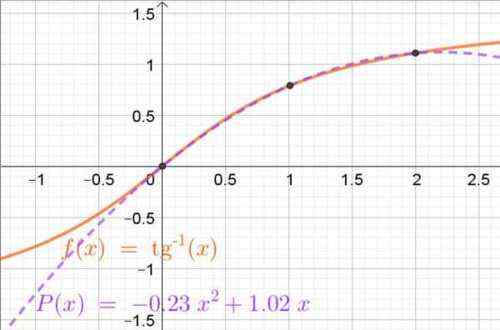Figur 4. Interpoling polynom oppnådd gjennom Lagrange-polynomer som tilnærmer Arc-Tangent-funksjonen i intervallet (0, 2). Interpolasjonspunkter vises også. Kilde: f. Zapata.

Øvelser

Oppgave 1

Få tilstrekkelige Lagrange -polynomer for å ha en tilnærming til funksjonen:

f (x) = sin (x)

I intervallet [0, π] og med fem interpolasjonspunkter.

Løsning

For det første bestemmes abscissen av interpolasjonspunktene, som er valgt like og inkludert endene av tilnærmingsintervallet. Med dette har du:

x₀= 0; x₁= π/4; x₂= π/2; x₃= 3 π/4; x₄= π.

Kan tjene deg: ulikhet i trekanten: demonstrasjon, eksempler, løste øvelser

Ettersom f (x) blir kansellert på de ekstreme punktene, vil det ikke være nødvendig å oppnå LaGrange L -polynomer l₀ og jeg₄.

Polynomer l₁, L₂ og jeg₃ er:

L₁ = [(x - x₀) / (X₁ - x₀)] [(x - x₂) / (X₁ - x₂)] [(x - x₃) / (X₁ - x₃)] [(x - x₄) / (X₁ - x₄)]

L₂ = [(x - x₀) / (X₂ - x₀)] [(x - x₁) / (X₂ - x₁)] [(x - x₃) / (X₂ - x₃)] [(x - x₄) / (X₂ - x₄)]

L₃ = [(x - x₀) / (X₃ - x₀)] [(x - x₁) / (X₃ - x₁)] [(x - x₂) / (X₃ - x₂)] [(x - x₄) / (X₃ - x₄)]

Nå erstatter vi verdien av abscissa:

L₁ = [(x - 0)/(π/4 - 0)] [(x - π/2)/(π/4 - π/2)] [(x - 3 π/4)/(π/4 - 3 π/4)] [(x - π)/(π/4 - π)]

L₂ = [(x - 0)/(π/2 - 0)] [(x - π/4)/(π/2 - π/4)] [(x - 3 π/4)/(π/2 - 3 π/4)] [(x - π)/(π/2 - π)]

L₃ = [(x - 0)/(3 π/4 - 0)] [(x - π/4)/(3 π/4 - π/4)] [(x - π/2)/(3 π/ 4 - π/2)] [(x - π)/(3 π/4 - π)]

Nevnerne er løst:

L₁ = [x/π/4] [(x - π/2)/( - π/4)] [(x - 3 π/4)/( - π/2)] [(x - π)/( - 3π/4)]

L₂ = [x/π/2] [(x - π/4)/(π/4)] [(x - 3 π/4)/( - π/4)] [(x - π)/( - π /2)]

L₃ = [x/(3 π/4)] [(x - π/4)/(π/2)] [(x - π/2)/(π/4)] [(x - π)/( - π/4)]

Det er forenklet og omgruppert for å oppnå:

L₁ = x (x - π/2) (x - 3 π/4) (x - π)/( - 3 π ⁴/128)

L₂ = x (x - π/4) (x - 3 π/4) (x - π)/(π ⁴/64)

L₃ = x (x - π/4) (x - π/2) (x - π)/( - 3 π ⁴/128)

Oppgave 2

Få interpolasjonspolynomet som nærmer seg Sen (x) -funksjonen i intervallet [0, π] med de fem interpolasjonspunktene valgt i oppgave 1 og deres respektive Lagrange -polynomer.

Løsning

Interpolasjonspolynomet er:

P (x) = sin (0) * l₀ + Sen (π/4) * l₁ + Sen (π/2) * l₂ + Sen (3π/4) * l₃ + Sen (π) * l4

Evaluering av bihule- og multipliseringsfunksjonen er:

P (x) = (√2/2) l₁ + 1 * l₂ + (-√2/2) l₃

Etter et vanskelig algebraisk verk, er interpolasjonspolynom:

P (x) = 2. 7481 x⁴ -femten. 138 x³ +23. 467 x² - 9. 5236 x

Referanser

1. Goodman, a. L. H. nitten nittiseks. Algebra og trigonometri med analytisk geometri. Pearson Education.
2. Harpe, p. d. (2000). Temaer i geometrisk gruppeteori. University of Chicago Press.
3. Hazewinkel, m. (2001). Lineær interpolasjon ", Encyclopedia of Mathematics.
4. Hoffmann, e. (2002). Til kronologi av interpolasjon: Fra eldgamle astronomi til moderne signal og bildebehandling. Fortsettelse av IEEE.
5. Wikipedia. Lagrange Polynomial interpolasjon. Gjenopprettet fra: Wikipedia.com